Отражение волны, падающей из вакуума, от границы с диэлектриком при наклонном падении и параллельной поляризации

Условия задачи. Электромагнитная волна частотой 100 МГц падает из вакуума на диэлектрическую плоскость с ε₂ = 2.25, μ₂ = 1, σ₂ = 0 под углом 45˚. Определить коэффициенты отражения и прохождения при параллельной поляризации падающей волны.

Решение. Для расчета коэффициентов отражения и прохождения необходимо определить волновые сопротивления сред и угол прохождения.

Для решения последней задачи необходимо определить волновые числа сред 1 и 2. Так как волна падает из вакуума, волновое число первой среды необходимо определить по формуле (3.12):

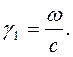
Так как во втором законе Снеллиуса используется отношение волновых чисел, дальше рассчитывать не целесообразно.

Волновое число второй среды необходимо определять по формуле (3.14):

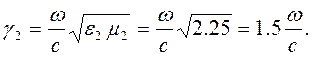
Далее можно вычислять угол прохождения. Однако в формулы для коэффициентов отражения и прохождения входит не угол прохождения, а его косинус. Поэтому представляется целесообразным преобразовать формулу (2.2) и уже затем проводить вычисления:

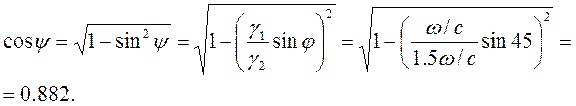
Далее необходимо вычислить волновое сопротивление Z₂ так как Z₁ известно и равно Z₀. Для этого воспользуемся формулой (3.13):

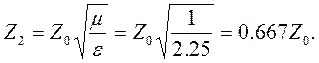
Все данные, необходимые для расчета модулей и фаз коэффициентов отражения и прохождения получены. Можно приступать к вычислениям. Однако предварительно вычислим cos φ = cos 45˚ = 0.707. Кроме того, необходимо учесть действительный характер обоих волновых сопротивлений, то есть отсутствие сдвигов фаз при отражении и прохождении. Поэтому для расчета коэффициентов отражения и прохождения используем формулы (2.15) и (2.16), заменив в них комплексные величины действительными:

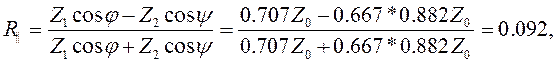
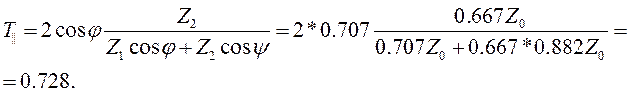
Задача решена.