Пусть событие А может произойти в любом из n повторных независимых испытаний с постоянной вероятностью р отличной от 0 и 1. пусть событие А не редкое, а количество испытаний достаточно велико, т.е. выполняются условия Муавра-Лапласа:
(1) 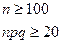 тогда справедлива локальная формула Муавра-Лапласа:
тогда справедлива локальная формула Муавра-Лапласа:
(2) 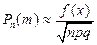 ;
; 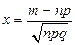 ;
; 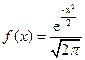 локальная функция Муавра-Лапласа
локальная функция Муавра-Лапласа
Свойства локальной функции Муавра-Лапласа.
1. 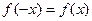
2. 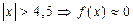
3. 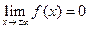
Пример:
Вероятность того, что посеянное семя взойдет равна 0,85. найти вероятность того, что ровно 213 из 250 семян взойдет.
Решение:
n = 250 > 100; m = 213; p = 0,85; q = 0,15;
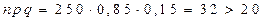
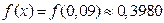
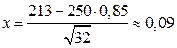
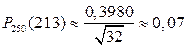
 2015-04-17
2015-04-17 319
319








