Формула Полячека –Хинчина

Если ρ <1, марковская цепь будет эргодична. В этом предположении можно получить матричное уравнение для определения стационарных вероятностей p_k, т.е. вероятностей того, что уходящее требование оставляет в СМО ровно k требований: 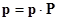, где вектор .

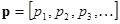Одной из наиболее важных характеристик СМО является значение средней длины очереди.

Для системы M/G/1 она дается формулой Полячека-Хинчина. Определим в пределе длину очереди как .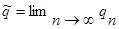

Анализируя два случая ухода требования С_n когда система остается непустой (Рис. 2) и случай ухода требования, когда система остается пустой (Рис.3),

Получаем два соотношения, связывающие случайные величины, определяющие число требований:

Для непустой .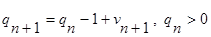

Для пустой .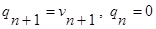

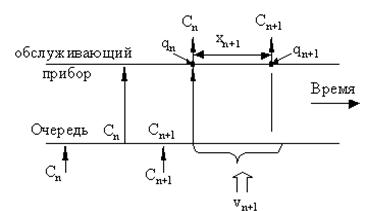
Рис. 2 Случай q_n >0.

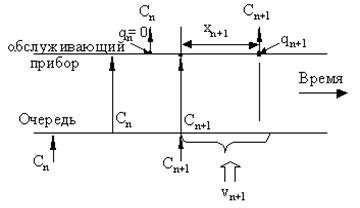
Рис. 3 Случай q_n =0.