Система типа G/G/1-этот класс систем предполагает, что как распределение интервалов времени между поступлением входных заявок-требований, так и распределение времени обслуживания в сервере описываются произвольными функциями плотности вероятности. Обозначим функцию плотности вероятности входного потока заявок a(t), а функцию плотности вероятности времени обслуживания b(x). Рассмотрим последовательность поступающих заявок на обслуживание - требований, пронумерованных индексами и вспомним обозначения, введенные ранее.
Cn - n -е требование, поступающее в систему,
tn - промежуток времени между поступлениями n -го и n -1 требований, плотность вероятности a(t) - не зависит от n.
xn - время обслуживания n -го требования, плотность вероятности b(x) -также не зависит от n,
wn - время ожидания n - го требования в очереди.
Напомним определение незавершенной работы для системы массового обслуживания. По определению незавершенная работа в каждый момент времени - это остаточное время, необходимое для освобождения системы от всех требований, находящихся в ней к этому моменту. Очевидно, что для системы G/G/1 значение незавершенной работы непосредственно перед поступлением n-го требования в точности равно времени wn. Таким образом, последовательность этих значений будет образовывать дискретную марковскую цепь, вероятности переходов которой могут быть определены по характеристикам входного потока и времени обслуживания. Зная эти переходные вероятности можно найти все характеристики изучаемой СМО. Рассмотрим два случая поступления требования Сn в систему - поступление в занятую систему (Рис. 1) и в свободную систему (Рис. 2).
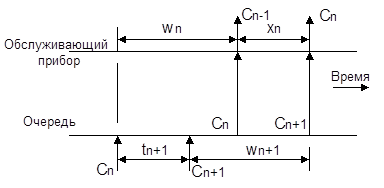
Рис. 1 Случай, когда требование Cn+1 поступает в занятую систему.
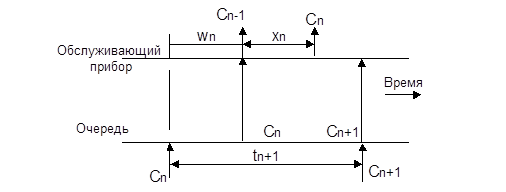
Рис. 2 Случай, когда требование Cn+1 поступает в свободную систему.
Нетрудно видеть, что для первого случая
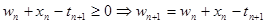 .
.
Для второго случая 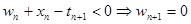 .
.
Определим случайную величину, равную разности между временем обслуживания требования с номером n и промежутком времени между поступлениями n +1 и n -го требований 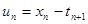 .
.
Фундаментальное свойство этой случайной величины состоит в том, что для стабильных СМО, т.е. имеющих стационарное распределение вероятностей состояний, ее математическое ожидание должно быть отрицательным. Смысл этого утверждения понятен из определения. Очевидно, что в среднем время обслуживания должно быть меньше времени между поступлениями соседних требований. Используя эту величину можно записать выражение для рекуррентного определения величин wn в компактном виде
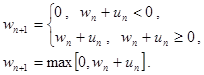
Решая это уравнение последовательно, начиная с нулевого требования, можно получить
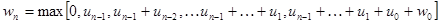 .
.
Условие стабильности М<un> <0, может быть записано в более привычной форме:
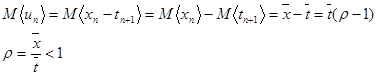
При выполнении этого условия будет существовать стационарное распределение вероятностей
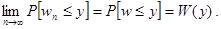
Эта функция распределения может быть записана через искомую плотность вероятности для времени ожидания в очереди
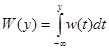 .
.
Для ее нахождения Линдли получил интегральное уравнение, носящее его имя.
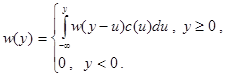
Функция c(u) определяется в свою очередь интегралом, похожим на свертку плотностей вероятности входного потока заявок и времени обслуживания
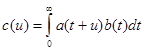 .
.
Решить уравнение Линдли в общем случае не удается. Если ввести преобразования Лапласа от функций плотности вероятности
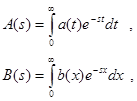
то удается записать:
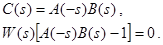
 2015-04-17
2015-04-17 1536
1536
