Под действием нагрузки элементы конструкции деформируются и
перемещаются. Перемещения происходят с ускорением, отчего возникают силы инерции.
При статическом действии нагрузка изменяется медленно. Ускорения
перемещений элементов конструкций, а, следовательно, и силы инерции весьма малы и поэтому их можно не учитывать.
При динамическом действии нагрузка изменяется быстро,
воздействует резко. Перемещения элементов конструкции происходят с заметным ускорением. Возникающие силы инерции существенны и подлежат учету.
Усилия, напряжения и перемещения от динамического действия
нагрузки в K д раз больше, чем от статического действия той же нагрузки:
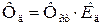 ,
,
где 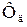 – фактор от динамического действия нагрузки;
– фактор от динамического действия нагрузки;
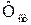 – фактор от статического действия той же нагрузки;
– фактор от статического действия той же нагрузки;
K д – коэффициент динамичности.
Для учета сил инерции при подъеме груза с ускорением
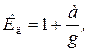
где a – ускорение, с которым движется груз;
g – ускорение свободного падения.
При ударном действии груза (без учета массы ударяемого элемента)
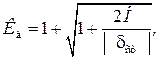
где H – высота падения груза;
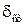 – перемещение точки приложения груза от его статического действия.
– перемещение точки приложения груза от его статического действия.
При продольном ударе 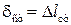 .
.
При поперечном (изгибающем) ударе 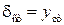 .
.
Пример 12
Груз весом 500 H падает с высоты 65 см на деревянную балку длиной 3 м и сечением 12 х 20 см (рис. 44). Проверить прочность балки, если 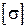 =10 МПа и Е = 1 ГПа.
=10 МПа и Е = 1 ГПа.
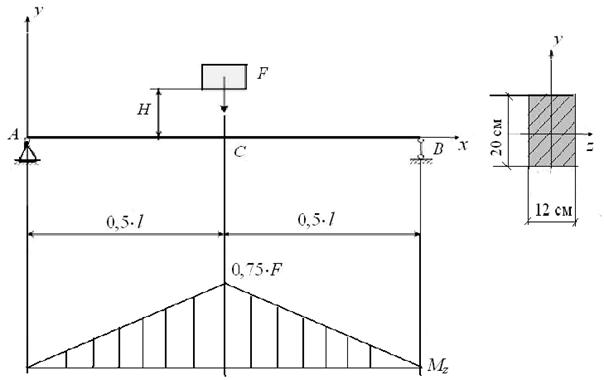
Рис. 44. Удар груза по балке
Балка подвергается поперечному (изгибающему) удару.
Условие прочности балки:
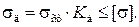
Напряжение в балке от статического действия груза:
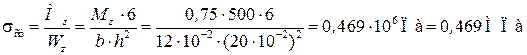 .
.
Для определения коэффициента динамичности необходимо знать величину прогиба в точке приложения груза от его статического действия. Воспользуемся методом начальных параметров и составим уравнение прогибов:
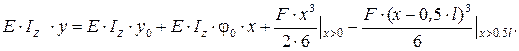
Так как начало отчета абсциссы х принято на опоре А, начальный
прогиб 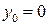 . Определим
. Определим 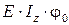 :
:
При 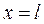
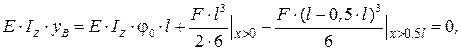
откуда 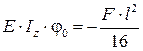 .
.
При 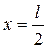
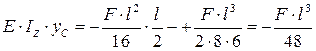 .
.
Прогиб при 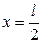 в точке С равен
в точке С равен
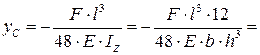
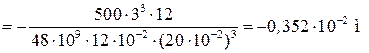 .
.
Коэффициент динамичности:
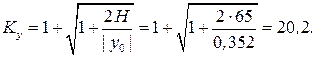
Динамическое напряжение:
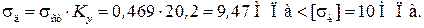
Прочность балки обеспечена.
Задача 12. Динамическое действие нагрузок
Произвести расчет балки при ударном действии груза весом  (рис.45). Материал балки – сталь,
(рис.45). Материал балки – сталь,  Данные к задаче приведены в табл. 16.
Данные к задаче приведены в табл. 16.
Таблица 16
Данные к задаче 12
| Номер строки | Номер схемы | Вес груза P, кН | Номер двутавра | Длина l, м | Высота падения H, м |
| I | 1,10 | 2,1 | |||
| II | 1.20 | 22а | 2,2 | ||
| III | 0.30 | 2,3 | |||
| IV | 0.40 | 24а | 2,4 | ||
| V | 0.50 | 2,5 | |||
| VI | 0.60 | 27а | 2,6 | ||
| VII | 0.70 | 2,7 | |||
| VIII | 0.80 | 30а | 2,8 | ||
| IX | 0.90 | 2,9 | |||
| X | 1,00 | 3,0 | |||
| в | б | а | в | в |
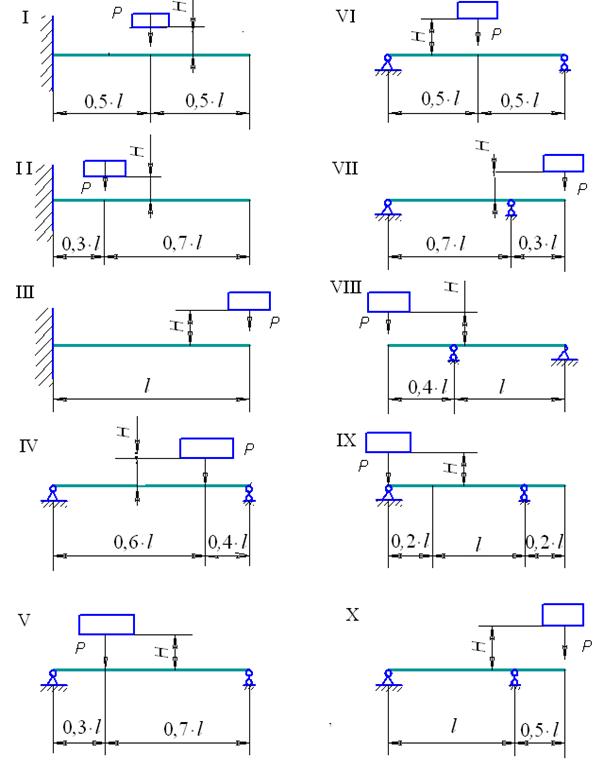
Рис. 45. Схемы балок к задаче 12
План решения задачи:
1) определить максимальное нормальное напряжение в балке при
статическом действии веса P;
2) определить прогиб балки в точке приложения веса P от
статического его действия;
3) вычислить динамический коэффициент;
4) вычислить максимальное нормальное напряжение от
динамического действия веса 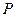 и сделать заключение о прочности балки;
и сделать заключение о прочности балки;
5) вычислить прогиб от динамического действия веса 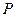 в точке его приложения.
в точке его приложения.
Примечание. Прогиб от статического действия груза весом P (в точке его приложения) определить по следующей формуле, взятой из справочника:
– в схемах I – III: 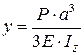 ;
;
– в схемах IV – VI: 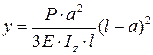 ;
;
– в схемах VII – X: 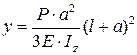 .
.
Вопросы для самоконтроля
1. Чем отличается динамическое нагружения от статического?
2. Что такое динамический коэффициент и чему он равен при подъеме груза с постоянным ускорением?
3. Что такое удар? Какие допущения используются при определении динамического коэффициента при ударе?
4. Запишите формулу для динамического коэффициента при ударе. Объясните влияние на него величины 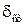 .
.
 2015-04-01
2015-04-01 2195
2195