2015-04-01
576
Рассмотрим движение буксируемого объекта (БО) под действием буксирной связи (рис 2.16). Отметим, что вектор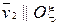 
. Обозначим: 
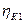- поперечная координата клюзовой точки К1; 
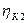- поперечная координата клюзовой точки К2; 
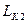- продольная координата клюзовой точки К2; 
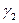- угол отклонения буксирной связи (БС), измеряемый от направления движением 
.
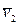Натяжение буксирной связи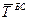 
разложим на продольную 
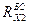и поперечную 
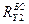составляющие. Продольная составляющая 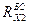является тягой БС, и обеспечивает продольное движение БО. Поперечная составляющая 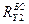вызывает движение в поперечном направлении и поворот корпуса БО по курсу под действием момента 
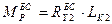, который является рулевым моментом.
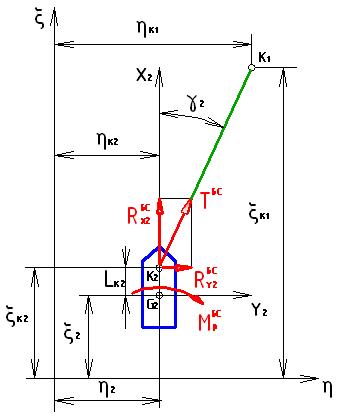
Рис 2.16. Схема действия буксирной связи
Сила 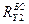и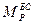 
появляются при отклонении БС на угол 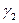в нужном направлении. Это достигается поперечным смещением клюзовой точки буксировщика К1.
Угол 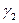назовем углом управления. Угол управления можно найти как:
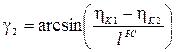. (2.63)
Знак угла 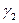будем считать положительным при отклонении БС вправо относительно БО.
|
|
|
Натяжение буксирной связи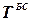 
зависит от отношения 
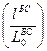, где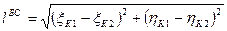 
, и от погонного веса БС. Натяжение может быть представлено жёсткостной характеристикой БС в виде формулы:
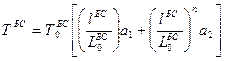, (2.64)
где: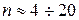 
- показатель степени; 
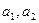- коэффициенты аппроксимации; 
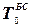- номинальное натяжение; 
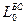- длина БС; 
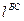- проекция БС на горизонтальную плоскость ватерлинии.
Определение реакций отдельной буксирной связи в общем виде представляет весьма сложную задачу, требующую интегрирования системы дифференциальных уравнений движения нити в частных производных. С целью упрощения задачи и уменьшения времени счёта, в первом приближении, можно ограничиться квазистатическим методом расчёта буксирной связи.
Для использования этого метода вводят упрощающие допущения:
- форма буксирной связи определяется силами тяжести и описывается уравнениями гибкой нерастяжимой нити;
- применима гипотеза квазистационарности;
- считается возможным применить принцип суперпозиции в определении результирующей реакции связи в клюзе;
- буксирная связь лежит в плоскости, содержащей оба клюза.
Рассмотрим буксирную связь. Концы связи лежат: точка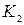 
- на буксируемом объекте и в неподвижной системе координат имеет координаты 
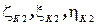, точка 
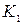- на буксире, координаты точки 
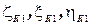. Уравнение гибкой связи имеет вид:
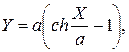(2.65)
где: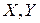 
- оси связанной со связью системы координат; 
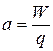- параметр связи; 
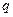- погонный вес единицы длины связи; 
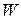- горизонтальная составляющая натяжения связи.
Это известное уравнение, описывающее положение равновесия гибкой и нерастяжимой однородной нити, находящейся в поле силы тяжести.
Стрелка прогиба нити f определится по формуле:
|
|
|
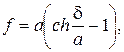(2.66)
где: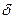 
- отстояние конца нити - точки 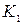, от начала координат.
Зная расстояние между концами буксирной связи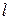 
, можно определить длину связи:
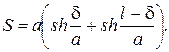(2.67)
Горизонтальная составляющая натяжения определяется по формуле:
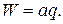(2.68)
Используя формулу (2.64), учтя при этом граничные условия для концов связи, натяжение в любой точки нити можно определить так:
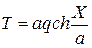. (2.69)
Величины натяжений в клюзовых точках будут соответственно равны:
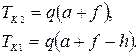(2.70)
Вертикальные составляющие натяжения в клюзах будут определяться как:
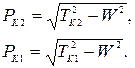(2.71)
В процессе движения буксирного состава, расстояние между объектами постоянно меняется, следовательно, изменяется и натяжение в БС. Поэтому в каждый момент времени при численном интегрировании уравнений (2.1) данный расчет должен выполняться.
Можно выделить 2 стратегии в управлении буксируемых систем:
1. Управление движением осуществляется из рубки буксировщика. Управление осуществляется с помощью курса следования буксировщика. Буксируемый объект должен двигаться вслед за буксировщиком по той же траектории в пределах допускаемых отклонений.
2. Управление осуществляется из ЦПУ буксируемого объекта путем задания с помощью буксировщика требуемого направления буксирной связи -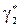 
.
В зависимости от принятой стратегии управления движением состава должны быть и выбраны характерные маневры состава.
