Решение. 1) Естественный свет, падая на грань призмы Николя (рис

1) Естественный свет, падая на грань призмы Николя (рис. 2.4), расщепляется вследствие двойного лучепреломления на два пучка: обыкновенный и необыкновенный. Оба пучка одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний необыкновенного пучка лежит в плоскости чертежа (плоскость главного сечения). Плоскость колебаний обыкновенного пучка перпендикулярна плоскости чертежа. Обыкновенный пучок света (о) вследствие полного отражения от границы АВ отбрасывается на зачерненную поверхность призмы и поглощается ею. Необыкновенный пучок (е) проходит через призму, уменьшая свою интенсивность вследствие поглощения. Таким образом, интенсивность света, прошедшего через первую призму,

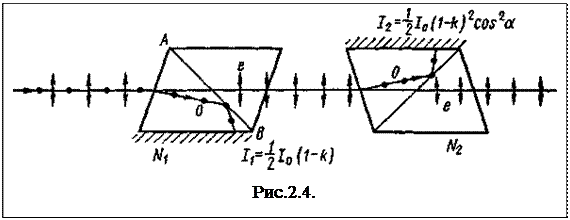I₁ = ½ I₀ (1- k).

Относительное уменьшение интенсивности света получим, разделив интенсивность I₀ естественного света, падающего на первый николь, на интенсивность I₁ поляризованного света:

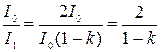. (2.9)

Произведем вычисления:

.

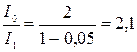Таким образом, интенсивность уменьшается в 2,1 раза.

2) Плоскополяризованный пучок света интенсивности I₁ падает на второй николь N₂ и также расщепляется на два пучка различной интенсивности: обыкновенный и необыкновенный. Обыкновенный пучок полностью погло­щается призмой, поэтому интенсивность его нас не интересует. Интенсивность I₂ необыкновенного пучка, вышедшего из призмы N₂, определяется законом Малюса (без учета поглощения света во втором николе):

I₂ = I₁ cos² α,

где α – угол между плоскостью колебаний в поляризованном пучке и плоскостью пропускания николя N₂.

Учитывая потери интенсивности на поглощение во втором николе, получаем

I₂ = I₁ (1- k)cos²α.

Искомое уменьшение интенсивности при прохождении света через оба николя найдем, разделив интенсивность I₀ естественного света на интенсивность I₂ света, прошедшего систему из двух николей:

.

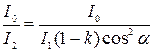Заменяя отношение I₀/I₁ его выражением по формуле (2.9), получаем

.

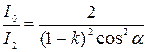Произведем вычисления:

.

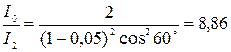Таким образом, после прохождения света через два николя интенсивность его уменьшится в 8,86 раза.

Пример 6. Плоскополяризованный монохроматический пучок света падает на поляроид и полностью им гасится. Когда на пути пучка поместили кварцевую пластину, интенсивность I пучка света после поляроида стала равна половине интенсивности пучка, падающего на поляроид. Определить 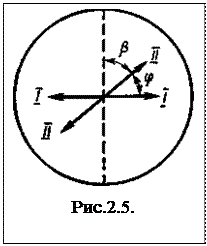минимальную толщину кварцевой пластины. Поглощением и отражением света поляроидом пренебречь, постоянную вращения α кварца принять равной 48,9 град/мм.

Решение. Полное гашение света поляроидом означает, что плоскость пропускания поляроида (штриховая линия на рис. 2.5) перпендикулярна плоскости колебаний (I—I) плоскополяризованного света, падающего на него. Введение кварцевой пластины приводит к повороту плоскости колебаний света на угол

φ = αl, (2.10)

где l – толщина пластины.

Зная, во сколько раз уменьшится интенсивность света при прохождении его через поляроид, определим угол β, который установится между плоскостью пропускания поляроида и новым направлением (II–II) плоскости колебаний падающего на поляроид плоскополяризованного света. Для этого воспользуемся законом Малюса

I = I₀ cos² β.

Заметив, что β = π /2-φ, можно написать

I = I₀ cos²(π /2-φ), или I = I₀ sin²φ. (2.11)

Из равенства (2.11) с учетом (2.10) получим αl = arcsin 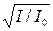, откуда искомая толщина пластины

.

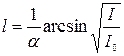Произведем вычисления во внесистемных единицах:

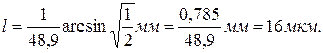
Пример 7. Определить импульс р и кинетическую энергию Т электрона, движущегося со скоростью u = 0,9 с, где с – скорость света в вакууме.

Решение. Импульсом частицы называется произ­ведение массы частицы на ее скорость:

p = mu. (2.12)

Т.к. скорость электрона близка к скорости света, то необходимо учесть зависимость массы от скорости, определяемую по формуле

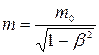, (2.13)

где m – масса движущейся частицы; m₀ – масса покоящейся частицы; β = u/c – скорость частицы, выраженная в долях скорости света.

Заменив в формуле (2.12) массу m ее выражением (2.13) и приняв во внимание, что u = сβ, получим выражение для релятивистского импульса:

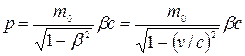. (2.14)

Произведем вычисления:

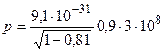кг·м/с = 5,6·10^-22 кг·м/с.

В релятивистской механике кинетическая энергия Т частицы определяется как разность между полной энергией Е и энергией покоя Е₀ этой частицы, т.е. Т = Е-Е₀. Т.к. Е = mс² и Е₀ = m₀c², то, учитывая зависимость массы от скорости, получаем

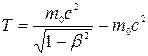или 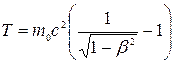. (2.15)

Произведем вычисления:

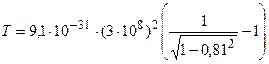= 1,06·10^-13 Дж.

Т.к. во внесистемных единицах m₀с² = 0,51 МэВ, вычисления упрощаются:

Т =0,51·1,29 МэВ=0,66 МэВ.

Пример 8. Определить релятивистский импульс электрона, обладающего кинетической энергией T = 5 МэВ.

Решение. Решение задачи сводится к установлению соотношения между релятивистским импульсом р частицы и ее кинетической энергией Т.

Сначала установим связь между релятивистским импульсом и полной энергией частицы. Полная энергия Е частицы прямо пропорциональна ее массе, т.е.

Е = mс². (2.16)

Зависимость массы от скорости определяется формулой

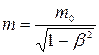. (2.17)

Заменив массу m в формуле (2.16) ее выражением (2.17), приняв во внимание, что m₀с² = E₀, получим

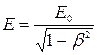. (2.18)

Возведя обе части равенства (2.18) в квадрат, найдем

,

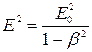откуда

E²-(βE)²=E₀². (2.19)

Очевидно, что

βE =(u/c) mc² = muc = pc.

Поэтому равенство (2.19) можно переписать в виде E² - р²с² = Е₀², откуда релятивистский импульс

.

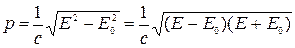Разность между полной энергией и энергией покоя есть кинетическая энергия Т частицы: Е-Е₀ = Т. Легко убедиться, что

Е+Е₀ = Т+2Е₀,

поэтому искомая связь между импульсом и кинетической энергией релятивистской частицы выразится формулой

.

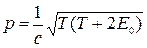Вычисления удобно провести в два приема: сначала найти числовое значение радикала во внесистемных еди­ницах, а затем перейти к вычислению в единицах СИ. Таким образом,

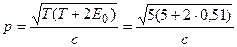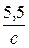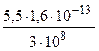= МэВ = Дж =
2,93·10^-21 кг·м/с

Пример 9. Длина волны, на которую приходится максимум энергии в спектре излучения черного тела, λ₀ = 0,58 мкм. Определить энергетическую светимость (излучательность) R_e поверхности тела.

Решение. Энергетическая светимость R_e абсолютно черного тела в соответствии с законом Стефана-Больцмана пропорциональна четвертой степени термодинамической температуры и выражается формулой

R_e=σT⁴, (2.20)

где σ – постоянная Стефана-Больцмана; Т – термодинамическая температура.

Температуру Т можно вычислить с помощью закона смещения Вина:

λ₀ = b / Т, (2.21)

где b – постоянная закона смещения Вина.

Используя формулы (2.20) и (2.21), получаем

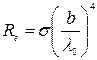. (2.22)

Произведем вычисления:

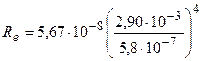= 3,54·10⁷ Вт/м² = 35,4 МВт/м².

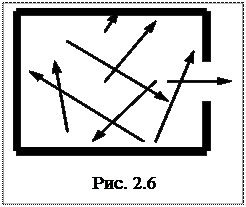
Пример 10. В модели абсолютно черного тела (см. рис. 2.6) температура стенок полости поддерживается равной 2000 К. Площадь отверстия S = 1 мм². Определить энергию, излучаемую через отверстие за 1 мин.

Решение. Воспользовавшись законом Стефана-Больцмана, находим искомую величину

Е = R·St = σT⁴St,

где, по условию, Т = 2000 К, t = 60 с, S = 10^{-6 м2}.

Произведя вычисления, получим ответ: Е = 54,4 Дж.

Пример 11. Максимум излучательной способности поверхности Солнца приходится на длину волны λ_max =0,5 мкм.

1) Определить температуру солнечной поверхности, считая, что она по своим свойствам близка к абсолютно черному телу.

2) Найти значение солнечной постоянной – интенсивности солнечного излучения вблизи Земли, за пределами ее атмосферы.

Решение.

1) Температуру солнечной поверхности определим с помощью закона Вина

T = b/ λ_max.

Произведя вычисления, получим Т = 5800 К.

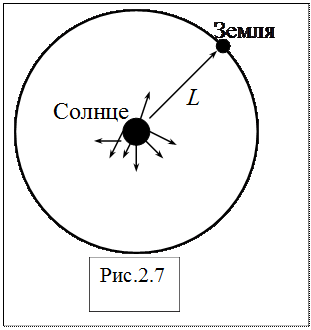
2) Значение солнечной постоянной С находим, разделив поток энергии Ф_E, излучаемый Солнцем по всем направлениям, на площадь поверхности сферы, радиус которой равен среднему расстоянию от Земли до Солнца L = 1,5*10¹¹м(рис. 6.3).

Поток энергии Ф_E равен произведению энергетической светимости R^* Солнца на площадь его поверхности, т.е. Ф_E =R·4πr_c², где r_c ≈ 7*10⁸м – радиус Солнца. Тогда

.

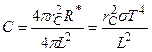Произведя вычисления, получим ответ:

C = 1400 Дж/(м²с), Т = 5800 К.

Пример 12. Определить максимальную скорость u_max фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны λ₁ =0,155 мкм; 2) γ -излучением с длиной волны λ₂ =1пм.

Решение. Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для фотоэффекта:

ε = A+T_max, (2.23)

где ε – энергия фотонов, падающих на поверхность металла; А – работа выхода; T_max – максимальная кинетическая энергия фотоэлектронов.

Энергия фотона вычисляется также по формуле

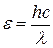, (2.24)

где h – постоянная Планка; с – скорость света в вакууме; λ – длина волны.

Кинетическая энергия электрона может быть выражена или по классической формуле

T=m₀u² /2, (2.25)

или по релятивистской формуле

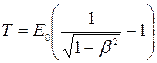, (2.26)

в зависимости от того, какая скорость сообщается фотоэлектрону. Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия ε фотона много меньше энергии покоя E₀ электрона, то может быть применена формула (2.25), если же ε сравнима по величине с E₀, то вычисление по формуле (2.25) приводит к ошибке, поэтому нужно пользоваться формулой (2.26).

1) Вычислим энергию фотона ультрафиолетового излучения по формуле (2.24):

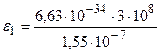= 1,28·10^-18 Дж,

или

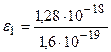= 8 эВ.

Полученная энергия фотона (8 эВ) много меньше энергии покоя электрона (0,51 МэВ). Следовательно, для данного случая кинетическая энергия фотоэлектрона в формуле (2.23) может быть выражена по классической формуле (2.25):

ε₁ = A+m₀u_max² /2,

откуда

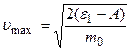. (2.27)

Проверим, дает ли полученная формула единицу скорости. Для этого в правую часть формулы (2.27) вместо символов величин подставим обозначения единиц:

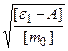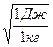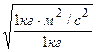= = =1 м/с.

Найденная единица является единицей скорости.

Подставив значения величин в формулу (2.27), найдем

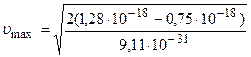= 1,08·10⁶ м/с.

2) Вычислим энергию фотона γ -излучения:

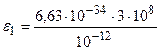= 1,99·10^-13 Дж,

или во внесистемных единицах

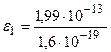= 1,24·10⁶ эВ = 1,24 МэВ.

Работа выхода электрона (А = 4,7 эВ) пренебрежимо мала по сравнению с энергией фотона (ε₂ = 1,24 МэВ), поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии фотона: Т_mах = ε₂ = 1,24 МэВ. Т.к. в данном случае кинетическая энергия электрона больше его энергии покоя, то для вычисления скорости электрона следует взять релятивистскую формулу кинетической энергии (2.26). Из этой формулы найдем

.

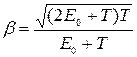Заметив, что u = cβ и T_max = ε₂, получим

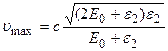
Произведем вычисления (Энергии Е₀ и ε₂ входят в формулу в виде отношения, поэтому их можно не выражать в единицах СИ):

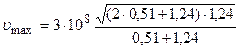= 2,85·10⁸ м/с.

Пример 13. В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол 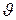= 90°. Энергия рассеянного фотона ε₂ = 0,4 МэВ. Определить энергию фотона ε₁ до рассеяния.

Решение. Для определения энергии первичного фотона воспользуемся формулой Комптона:

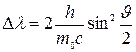. (2.28)

где Δλ=λ₂-λ₁ – изменение длины волны фотона в результате рассеяния на свободном электроне; h – постоянная Планка; m₀ – масса покоя электрона; с – скорость света в вакууме; 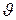– угол рассеяния фотона.

Преобразуем формулу (2.28):

1) заменим в ней Δλ на λ₂-λ₁;

2) выразим длины волн λ₁ и λ₂ через энергии ε₁ и ε₂ соответствующих фотонов, воспользовавшись формулой ε = hс/λ;

3) умножим числитель и знаменатель правой части формулы на с. Тогда

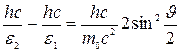. (2.29)

Сократим на hс и выразим из этой формулы искомую энергию:

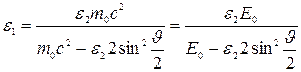, (2.30)

где Е₀ = m₀с² – энергия покоя электрона.

Вычисления по формуле (2.30) удобнее вести во внесистемных единицах. Т.к. для электрона Е₀ = 0,511 МэВ, то

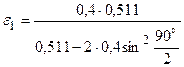=1,85 МэВ.

Пример 14. Фотон с импульсом р = 1,02 МэВ/с, где с - скорость света, рассеялся на покоившемся свободном электроне, в результате чего импульс фотона стал равным р ' = 0,255 МэВ/с.

1) Под каким углом рассеялся фотон?

2) Какая доля энергии первичного фотона приходится на кинетическую энергию электрона отдачи?