Задание 1. Параметризация регрессионных уравнений.
Классический подход к оцениванию параметров линейных зависимостей (параметризации регрессионных уравнений) рассматривается на примере линейной парной регрессии
y = b0 + b1x + e
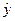 = yx = b0 + b1x,
= yx = b0 + b1x,
где y – фактическое значение результативного признака;
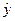 или yx – теоретические значение результативного признака, найденные из уравнения регрессии, путём подстановки в него фактических значений фактора х;
или yx – теоретические значение результативного признака, найденные из уравнения регрессии, путём подстановки в него фактических значений фактора х;
b0, b1 – параметры (коэффициенты) уравнения регрессии;
e - случайная составляющая (возмущение, ошибка), характеризующая отклонение фактического значения результативного признака от теоретического, найденного по уравнению регрессии.
Имеются два ряда эмпирических (полученных из опыта) данных x (x 1, x 2, …, x n) и y (y 1, y 2, …, y n), отображение соответствующих им точек с координатами (xi, yi), где i = 1, 2, …, n, на координатной плоскости называется полем корреляции.
По расположению эмпирических точек можно предположить вид корреляционной зависимости. Например, наличие линейной корреляционной зависимости между переменными х и у.
Построение линейной регрессии предполагает оценку её параметров b0 и b1 с помощью метода наименьших квадратов (МНК).
Согласно МНК неизвестные параметры b0 и b1 получают таким образом, чтобы сумма квадратов отклонений фактических значений yi от значений 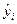 , найденных по уравнению регрессии была бы минимальной
, найденных по уравнению регрессии была бы минимальной
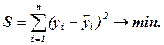
Таким образом, из множества возможностей, положение линии регрессии на графике выбирается таким образом, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была минимальной
ei = yi – 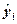 ,
,
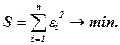
Для поиска минимума функции, необходимо вычислить частные производные по каждому из параметров b0 и b1 и приравнять их к нулю
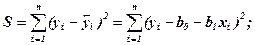
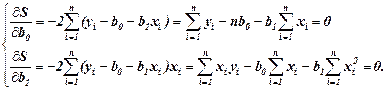
В результате преобразований получается следующая система нормальных уравнений для оценки параметров b0 и b1
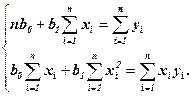
Искомые оценки параметров b0 и b1 находят решая систему нормальных уравнений методом подстановки, последовательного исключения переменных либо методом определителей. Так,
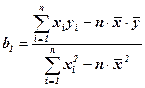 .
.
Разделив обе части уравнений системы на n, получим
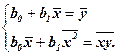
Из первого уравнения системы получим
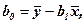
После подстановки во второе уравнение получим
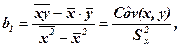
где 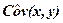 – выборочная ковариация признаков (корреляционный момент)
– выборочная ковариация признаков (корреляционный момент)
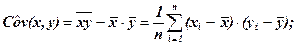
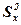 – дисперсия признака х
– дисперсия признака х
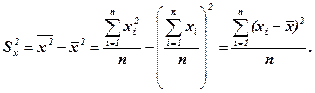
Решение системы нормальных уравнений может быть осуществлено методом определителей
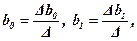
где D – определитель системы;
Db 0, Db1 – частные определители, получаемые путём замены соответствующего столбца матрицы определителя системы данными правой части исходной системы нормальных уравнений;
 ,
, 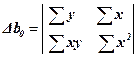 ,
, 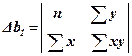 .
.
Данные о стоимости основных фондов и продукции предприятий (фирм), млн руб.
| фирма | x | y | S xy | x 2 | y 2 |
| 201,6 | 1011,3 | 203878,1 | 40642,56 | ||
| 242,6 | 1490,4 | 58854,76 | |||
| 255,4 | 1024,5 | 261657,3 | 65229,16 | ||
| 323,7 | 559,9 | 181239,6 | 104781,7 | ||
| 331,9 | 1195,1 | 396653,7 | 110157,6 | ||
| 384,6 | 1050,1 | 403868,5 | 147917,2 | ||
| 397,7 | 1482,8 | 589709,6 | 158165,3 | ||
| 450,7 | 1151,7 | 519071,2 | 203130,5 | ||
| 457,6 | 1020,6 | 467026,6 | 209397,8 | ||
| 515,3 | 849214,4 | 265534,1 | |||
| 533,8 | 2441,9 | 284942,4 | |||
| 587,8 | 1424,6 | 837379,9 | 345508,8 | ||
| 614,9 | 1095,4 | 673561,5 | |||
| 655,1 | 1278,5 | 837545,4 | |||
| 720,1 | 2091,4 | ||||
| 741,5 | 2403,5 | 549822,3 | |||
| 760,9 | 578968,8 | ||||
| 814,1 | 2042,3 | 662758,8 | |||
| 859,2 | 1607,9 | 738224,6 | |||
| 1683,2 | |||||
| 953,8 | 909734,4 | ||||
| 1092,6 | 3063,9 | ||||
| 1148,9 | 2048,4 | ||||
| 1247,5 | 2034,4 | ||||
| 1253,1 | 2435,9 | ||||
| 1873,5 | 3082,1 | ||||
| Сумма | 18348,9 | 43906,8 |
Построим корреляционное поле и проведём линию регрессии
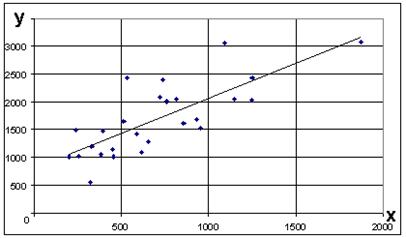
Для нахождения параметров уравнения регрессии используем функцию Excel МОПРЕД, позволяющую рассчитать определитель матрицы
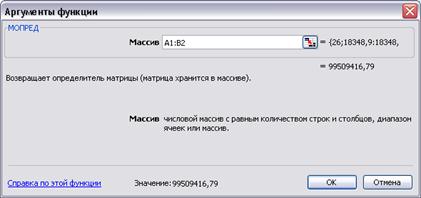
Так, определитель системы в целом равен D = =99509416,79, частный определитель Db 0 = 79005533565, частный определитель Db 1 = 126165393,5. 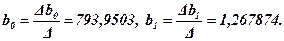
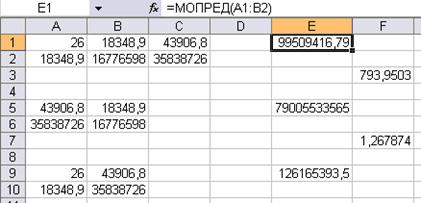
Уравнение регрессии имеет вид
y = 793,9503 + 1,26 × х + e.
 2015-04-01
2015-04-01 314
314








