Статические модели управления запасами применяются в тех случаях, когда для удовлетворения спроса может подаваться только один заказ на закупку товара. Заказы на пополнение запаса либо не возможны, либо сопряжены с очень большими издержками. Пример: торговля мороженым на празднике мороженного; закупка сырья для производства ультрамодной продукции и т.п. [8].
Однако применение статических моделей не ограничивается короткими промежутками времени. Эти модели могут применяться также в случае закупки запасных частей для специального оборудования.
Статические модели также позволяют определить начальные запасы для новых продуктов.
Формирование модели для решения статической задачи рассмотрим на практическом примере.
Допустим, продавец занимается реализацией новогодних елок. Перед ним стоит задача определения количества деревьев, которое нужно закупить с целью последующей перепродажи при условии, что в процессе реализации (примерно 2 недели до Нового года) нельзя будет разместить новый заказ, а сразу же после праздника – елки будет невозможно реализовать даже по сниженным ценам.
Для решения задачи необходимо получить информацию о возможном спросе на продукцию, чтобы определить объем продаж.
Информация о спросе может быть получена несколькими способами:
1. Посредством наблюдения за спросом в предыдущие периоды. В этом случае осуществляется статистическая обработка данных по спросу за ряд лет и определяется закон распределения спроса.
2. Опрос экспертов (они, как правило, дают дискретную оценку спроса).
3. Изучение официальной статистики (средние значения продаж определенной продукции за определенный период в данном регионе).
Вернемся к примеру с новогодними елками. Пусть продавец в течение нескольких лет собирал информацию о продажах новогодних елок, причем использовал как собственные данные, так и сведения о продажах конкурентов.
Собранные продавцом данные о продажах елок приведены в табл. 4.1.
Допустим, что каждая проданная елка приносит прибыль, равную G ден. ед., а из-за каждой непроданной елки торговец теряет С ден. ед. Допустим также, что издержки выполнения заказа и затраты на хранение елок незначительны. Тогда чистая прибыль от реализации S -й елки будет определяться по формуле [8]:
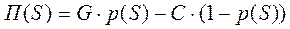 , (4.1)
, (4.1)
где р(S) - вероятность того, что S -я единица товара будет продана.
Из формулы (4.1) вытекает и условие прибыльности S -й единицы товара:
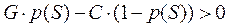 (4.2)
(4.2)
Выражение (4.2) может быть представлено в виде:
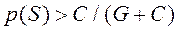 (4.3)
(4.3)
Таким образом, торговцу необходимо закупать такое максимальное количество товара (S), при котором вероятность продажи этого или большего количества продукции будет соответствовать условию (4.3). То есть продавец максимизирует свою прибыль в том случае, когда чистая прибыль от реализации S -й единицы товара будет равна 0.
Пример 4.1:
Если предположить, что продавец приобретает елки в среднем по цене 56 руб. за штуку (без учета метража), а продажа каждой елки в среднем приносит ему прибыль в размере 180 руб., то исходя из условия (4.3) продавцу выгодно закупать такое количество елок, для которого:
p(S)>56/(180+56)
p(S) >0,237
Этой вероятности соответствует 150 елок или интервал 141-160 елок (табл. 4.1).
Таблица 4.1
Результат решения задачи «о новогодней елке»
| Границы интервала | Середина интервала, Si | Частота продаж -ni | Относительная частота ni/∑ni (частость) | Накопленная частота, F(S) | Вероятность продажи S-й единицы p(S)=1-F(S) | Ожидаемая прибыль при продаже S-й единицыG∙p(S) | Ожидаемый убыток при непродаже S-й единицыC∙(1-p(S)) | Чистая прибыль при продажеS-й единицы товара |
| 40-60 | 0,025 | 0,025 | 0,975 | 175,5 | 1,4 | |||
| 61-80 | 0,0875 | 0,1125 | 0,8875 | 159,75 | 6,3 | |||
| 81-100 | 0,15 | 0,2625 | 0,7375 | 132,75 | 14,7 | |||
| 101-120 | 0,2 | 0,4625 | 0,5375 | 96,75 | 25,9 | |||
| 121-140 | 0,175 | 0,6375 | 0,3625 | 65,25 | 35,7 | |||
| 141-160 | 0,125 | 0,7625 | 0,2375 | 42,75 | 42,7 | |||
| 161-180 | 0,1125 | 0,875 | 0,125 | 22,5 | -27 | |||
| 181-200 | 0,075 | 0,95 | 0,05 | 53,2 | -44 | |||
| 200 и более | 0,05 | -56 | ||||||
Необходимо отметить, что спрос может быть как дискретной, так и непрерывной случайной величиной.
Дискретной называют случайную величину, которая принимает конечное или счетное число значений, которые можно пронумеровать натуральными числами), то у него не будет плотности распределения [13, 22].
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала [13, 22].
Если спрос распределен дискретно, то данные по нему могут быть заданы в табличной форме так, как это показано в табл. 4.1, и для решения статической задачи в данном случае могут использоваться формулы (4.1)-(4.4).
Если спрос распределен непрерывно, то в этом случае он будет за даваться определенной функцией распределения (F(x)) и плотностью распределения (f(х)).
На рис. 4.1. показана ситуация нормально распределенного спроса.
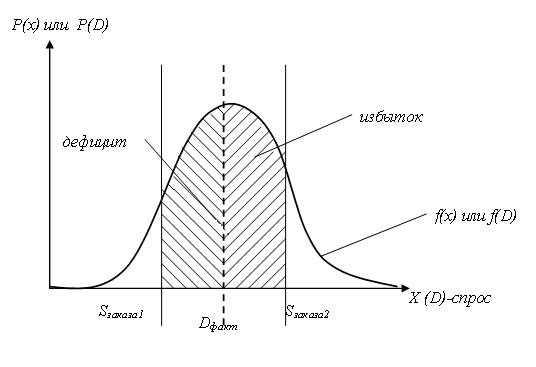
f (D) – плотность распределения спроса
Рис. 4.1. Плотность нормально распределенного спроса
Дефицит возникает в том случае, когда объем заказа (Sзаказа) оказывается меньше фактической потребности (Dфакт). Если объем заказа превышает потребность, то соответственно наблюдается избыточный запас. Величину дефицита и профицита (избытка) в условиях непрерывно распределенного случайного спроса можно определить, рассчитав соответствующую площадь под кривой плотности распределения – см. рис. 4.1.
При определении оптимального объема запаса в качестве целевой функции рассматривается функция суммарных затрат, связанных с запасом [38]:
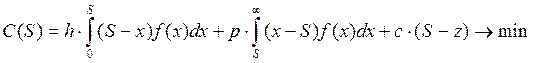 , (4.4)
, (4.4)
где S – предполагаемый объем запаса (партии закупки);
x – случайная величина, характеризующая спрос на продукцию;
h – издержки, связанные с содержанием единицы избыточного запаса (нереализованной продукции);
p – потери от дефицита (штрафы), связанные с нехваткой единицы продукции;
c – цена приобретения единицы продукции;
z – остаток запаса предыдущего периода;
f(x) – функция плотности распределения спроса.
Для нахождения оптимального уровня запаса (S) необходимо взять первую производную функции затрат по S и приравнять ее к нулю:
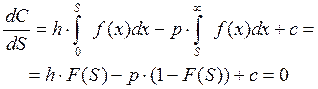 (4.5)
(4.5)
Из выражения (4.5) получаем уравнение для нахождения оптимального уровня запаса [38]:
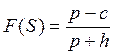 , (4.6)
, (4.6)
где F(S) или F(x) – интегральная функция распределения спроса.
В работе [38] приводятся результаты решения уравнения (4.6) для некоторых видов законов распределения спроса (табл. 4.2).
Таблица 4.2
Значения оптимального уровня запаса для различных законов распределения спроса
| Вид закона распределения спроса | Функция распределения спроса | Выражение для нахождения оптимального размера запаса – Sopt |
| Нормальный закон: | 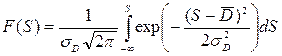 | 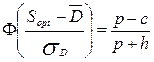 , где , где 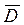 - средний спрос; σD – СКО спроса - средний спрос; σD – СКО спроса |
| Показательный закон: | 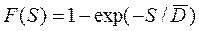 | 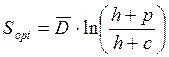 |
| Распределение Релея: | 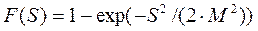 , где , где 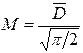 - параметр распределения Релея - параметр распределения Релея | 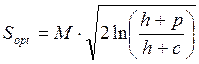 |
| Распределение Вейбулла: | 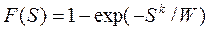 , где k и W – параметры распределения Вейбулла , где k и W – параметры распределения Вейбулла | 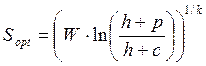 |
 2015-04-01
2015-04-01 1541
1541
