Логические сети

При математическом описании тех или иных физических объектов, как правило, отвлекаются от целого ряда второстепенных факторов и процессов, действующих в этих физических объектах. Такая абстракция необходима для создания общей математической теории для целого класса родственных между собой физических процессов.

Целью настоящей главы является разработка методов и способов анализа и синтеза физических устройств, предназначенных для переработки дискретной информации.

Мы будем изучать не сами эти устройства, а некоторым образом адекватные им математические схемы. Эта адекватность выражается в том, что работа обеих схем (физической, реально действующей и математической абстрактной) описывается с помощью одних и тех же математических соотношений.

Такую адекватную математическую схему мы будем называть логической сетью.

Дадим более четкое определение понятия логической сети. Пусть мы имеем конечное множество А:

A = {1,2,3, …, m };

И пусть нам задано множество В, элементами которого являются упорядоченные пары элементов множества А:

B = {(i, j)}.

Здесь i, j — любые из элементов множества A, i≠j. Пусть, наконец, нам задано некоторое множество F, элементами которого являются логические функции

F = { f ₁, f ₂, …, f _y}

Установим однозначное соответствие между множествами F и A, т. е. сопоставим каждому элементу множества А один из элементов множества F.

Определение 0. Совокупность множеств А и В совместно с однозначным отображением множества F на множество А называется логической сетью.

Определенное таким образом понятие логической сети совпадает с понятием ориентированного нагруженного графа. Геометрической интерпретацией логической сети служит некоторая схема логической сети, которая строится следующим образом. На плоскости в произвольном порядке располагаются элементы множества А. (Для их обозначения будем использовать кружок). Эти элементы называются вершинами графа (рисунок 6.1, a).

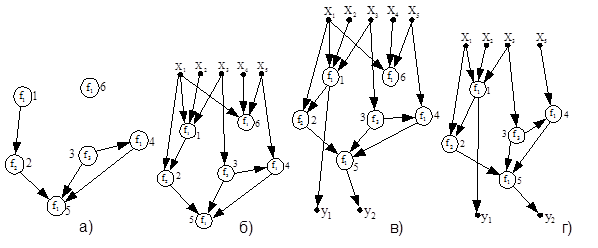
Рисунок 6.1 – Вершины графа

Символ соответствующего данному кружку элемента i (т.е. номер) пишется справа от этого кружка. Внутри кружка вписывается элемент множества F, сопоставленный при отображении F на А элементу, соответствующему данному кружку. Наконец, все кружки соединяются между собой ориентированными стрелками согласно элементам множества В. Элементу (i, j) соответствует стрелка, идущая от кружка, сопоставленного элементу i, к кружку, сопоставленному элементу j. Эти стрелки носят название ребер графа.

Пример 1. Пусть

A = {1,2,3,4,5,6};

B = {(1,2),(3,4),(4,5),(2,5),(3,5)};

F = { f ₁, f ₂, f ₃}

и отображение F на А задано как

f ₁ → 1,4,5,6;

f ₂ → 2;

f ₃ →3.

Соответствующая схема заданной логической сети показана на рисунке 6.1, а..

Введем в рассмотрение множество аргументов

X = { x ₁, x ₂, …, x_n }.

Произведем теперь отображение некоторых подмножеств множества X на некоторые элементы множества А

X* → a_i,

где X* некоторое подмножество множества X. При геометрической интерпретации элементы множества X будем изображать жирными точками и называть входами схемы логической сети. Задание отображения подмножества X* на элементы a_i эквивалентно заданию множества С следующего вида:

C = {(X *, i)}/

Геометрической интерпретацией множества С являются ребра, проведенные из соответствующих входов схемы к вершинам графа, сопоставленным нужным элементам множества А.

Пример 2. Для логической сети на рисунке 6.1, а задано:

X = { x ₁, x ₂, x ₃, x ₄, x ₆};

C = {(x ₁, x ₂, x ₃; 1), (x ₁; 2), (x ₃; 3), (x ₅; 4), (x ₁, x ₄, x ₅; 6)}.

Соответствующая схема логической сети приведена на рисунке 6.1, б.

Потребуем теперь, чтобы элементы множества В обладали тем свойством, что для всякого элемента (i, j) i < j. Подобную логическую сеть назовем упорядоченной или логической сетью без обратных связей.

Теперь ограничим отображение множества F на А следующим образом. Потребуем, чтобы функция f_j,, сопоставляемая вершине с номером i, зависела бы от стольких аргументов, сколько ребер входит в данную вершину. Эквивалентным требованием является ограничение на элементы множеств В и С при заданном отображении F на А. Суммарное число пар вида (i, j)и (x_i, j) не должно превышать числа аргументов, имеющихся у функции, сопоставленной вершине с номером j. Логическую сеть, для которой выполнено это требование, назовем правильной.

Определение 0. Упорядоченная и правильная логическая сеть называется регулярной логической сетью (РЛС).

В дальнейшем будем рассматривать только правильные логические сети, а на протяжении этого раздела ограничимся рассмотрением только регулярных логических сетей. Рассмотрим, наконец, множество выходов

Y = { y ₁, y ₂, …, y_k }.

Произведем теперь взаимно однозначное отображение некоторого подмножества А* множества А на множество Y. Для возможности такого отображения, очевидно, необходимо выполнение неравенства k≤ m*, где m* — число элементов А*. Геометрической интерпретацией этого отображения будут ребра, направленные от элементов множества А* к соответствующим элементам множества Y. Элементы множества Y, как и элементы множества X, будем обозначать жирными точками.

Пример 3. Для логической сети на рисунке 6.1, б определено множество

Y = { y ₁, y ₂}.

и взаимно однозначное отображение

1 ←→ y ₁,

5 ←→ y ₂

Соответствующая схема логической сети приведена на рисунке 6.1, в.

После отображения некоторых вершин графа на множество Y в графе могут остаться вершины, из которых не выходит ни одно ребро. Такие вершины назовем тупиковыми и исключим их, а также ребра, идущие к ним. Оставшуюся после этого схему логической сети будем называть логическим многополюсником. Если множество X содержит п элементов, а множество У — k элементов, то такой логический многополюсник будем называть логическим (п, k)–полюсником.

Пример 4. Для регулярной логической схемы, данной на рисунке 6.1, в, вершина 6 является тупиковой. После ее удаления остается логический (5,2)-полюсник, вход х₄ у которого является фиктивным, и поэтому он опущен на схеме логической сети (рисунок 6.1, г).

Теория логических сетей включает в себя целый ряд различных разделов. В этих разделах изучаются вопросы, связанные с поисками методов эффективного преобразования информации, оптимальным кодированием, геометрией сетей, проблемами надежности сети и т. д. Из всего множества этих проблем мы рассмотрим только проблемы, связанные с анализом и синтезом логической сети.