Теорема анализа и эквивалентные схемы

Рассмотрим решение задачи получения общей логической функции (или системы функций), отражающей структуру логической сети. Для логического (п, k)-полюсника эти функции имеют вид:

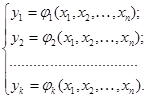
(6.1)

Система (6.1) называется системой собственных функций (п, k)-лолюсника. Таким образом, задача анализа данной схемы логической сети сводится к написанию системы собственных функций для этой сети.

Пример 5. На рисунке 6.2 показана схема логического (4,2)-полюсника. Система собственных функций для этой сети будет:

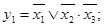
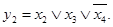
Пример 6. На рисунке 6.3показана схема логического (4,2)-полюсника, система собственных функций которого имеет вид:

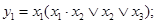
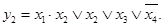
Произведем преобразование этой системы функций:

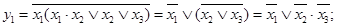
Совпадение преобразованных собственных функций примера 6 с соответствующими функциями примера 5 показывает, что с точки зрения логического описания эти схемы логических сетей совпадают.

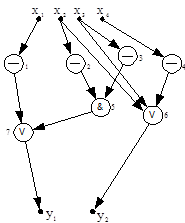
Рисунок 6.2 – Пример №5

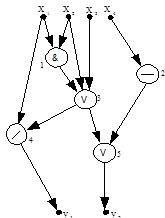
Рисунок 6.3 – Пример №6

Определение 0. Две схемы логических сетей, у которых собственные функции эквивалентны, т. е. могут быть получены одна из другой с помощью эквивалентных преобразований, называются эквивалентными.

Схемы (4, 2)-полюсников на рисунках 6.2 и 6.3 эквивалентны между собой. Подчеркнем, что собственные функции не определяют вид схемы логической сети, т. е. не обязательно являются структурными функциями. Эти функции описывают лишь логическую связь между множеством входов и множеством выходов схемы.

В дальнейшем удобно несколько изменить правила геометрической интерпретации логических сетей. Во-первых, вместо обозначений вершин графа с помощью кружков будем использовать стандартные обозначения для наиболее часто встречающихся логических функций (эти обозначения приведены на рисунке 6.4), при этом будем предполагать, что все логические элементы, кроме элемента, моделирующего функцию отрицания, имеют два входа (рисунок 6.4).

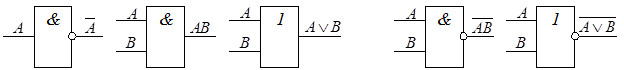
Рисунок 6.4 – Основные обозначения логических функций

Кроме того, в дальнейшем не будем указывать множество вершин, сопоставляемых множествам X и Y. Эти вершины будут просто подразумеваться. Соответствующие стрелки, идущие от вершин множества X к вершинам множества А и от вершин множества А к вершинам множества Y, будут обрываться, а у места обрыва будет указываться вершина X или Y, с которой связано это ребро. Наконец, не будем ставить там, где это не вызывается особой необходимостью, номера вершин А.

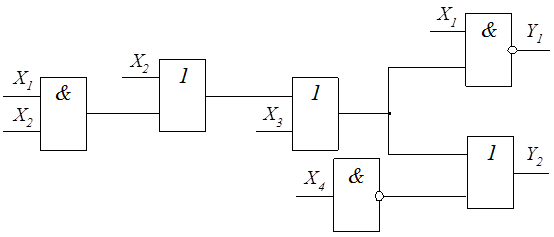
Рисунок 6.5 – Схема логической сети

В соответствии с этими изменениями на рисунке 6.5 изображена схема логической сети, представленная ранее на рисунке 6.2.

Подчеркнем, что анализ схемы дает однозначное написание ее собственных функций и это написание отражает структуру схемы. Особенно наглядна связь между написанием собственных функций и структурой схемы, если пользоваться скобочной формой записи.

Пример 7. Для схемы, изображенной на рисунке 6.5, скобочная запись "от входов к выходам" выглядит следующим образом:

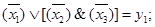
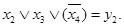
Эта запись полностью определяет структуру соответствующей схемы логической сети. Другими словами, для скобочной записи собственных функций «от входов к выходам» можно установить взаимнооднозначное соответствие между этой записью и структурой схемы логической сети.

Анализ реальных схем с точки зрения логики их работы проводится в два этапа. Сначала из имеющейся принципиальной схемы удаляются все несущественные, вспомогательные элементы, которые не влияют на логику работы схемы, а служат для обеспечения устойчивости работы схемы, нормальной крутизны фронтов импульсов и т. д. После этого получаем схему, состоящую лишь из элементов, выполняющих логические функции, и связей между ними. Такая схема эквивалентна заданию некоторой схемы логической сети. Для ее анализа можно воспользоваться вышеизложенными соображениями.