Если 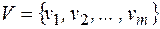 – оптимальный двоичный код при распределении
– оптимальный двоичный код при распределении 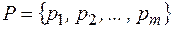 , и некоторая вероятность
, и некоторая вероятность 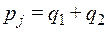 , причем
, причем
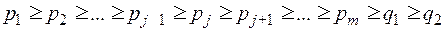 ,
,
то код 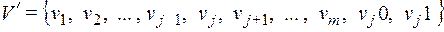 так же является оптимальным при распределении
так же является оптимальным при распределении
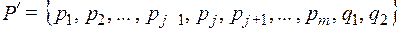 .
.
Код 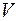 является расширением кода
является расширением кода 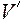 .
.
Пример 4.
Построение оптимального кода Хаффмена заключаются в следующем. Пусть в упорядоченном по невозрастанию вероятностей списке две последние вероятности 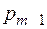 и
и 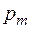 . Эти вероятности из списка исключаются, а их сумма вставляется в список таким образом, чтобы вероятности по-прежнему не убывали. Делаем так, пока в списке не останется две вероятности. Первой из них присваивается символ 0, второй – символ 1. Получаем оптимальный код, состоящий из 2 кодовых слов. Далее, используя теорему расширяем его до кода из 3 слов, и т. д. Пока не получим список исходных вероятностей.
. Эти вероятности из списка исключаются, а их сумма вставляется в список таким образом, чтобы вероятности по-прежнему не убывали. Делаем так, пока в списке не останется две вероятности. Первой из них присваивается символ 0, второй – символ 1. Получаем оптимальный код, состоящий из 2 кодовых слов. Далее, используя теорему расширяем его до кода из 3 слов, и т. д. Пока не получим список исходных вероятностей.
Ниже приведен пример построения кода Хаффмена для распределения Р = {0.5, 0.2, 0.2, 0.1}.
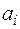
| 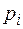
|  
|  
|    
|  
| 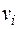
| ||||||||||
| a | 0,5 | 0,5 | 0,5 | |||||||||||||
| b | 0,2 | 0,3 |  
| 0,5 | 
| |||||||||||
| c | 0,2 |  
| 0,2 | 
| ||||||||||||
| d | 0,1 |
Найдем стоимость полученного кода.
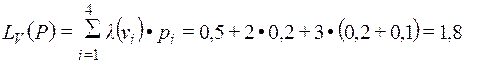 .
.
Рассмотрим равномерный код с обнаружением и исправлением ошибок.
Однозначной ошибкойтипазамещения называют результат замены одного из символов 0 на 1 или 1 на 0. Кратностью ошибки s называется число ошибок одного типа. Например, если передаваемое слово 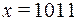 , а на приемной станции получено
, а на приемной станции получено 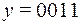 , то в слове произошла ошибка типа замещения.
, то в слове произошла ошибка типа замещения.
Функция Хемминга 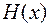 , задается на двоичных векторах
, задается на двоичных векторах 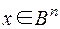 . Это вектор минимальной длины l, полученный в результате покоординатного сложения по модулю 2 двоичных кодов номеров тех координат вектора х, которые равны 1.
. Это вектор минимальной длины l, полученный в результате покоординатного сложения по модулю 2 двоичных кодов номеров тех координат вектора х, которые равны 1.
Здесь l – та длина двоичного кода, которой достаточно, чтобы закодировать номера всех координат слова х.
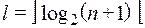 .
.
Таким образом,
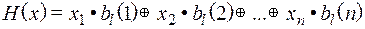 .
.
Пример 5.
Найти функцию Хемминга для двоичного слова 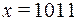 . Так как
. Так как 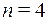 , то
, то 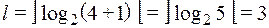 . Найдем двоичные коды длины 3 для всех номеров координат слова х.
. Найдем двоичные коды длины 3 для всех номеров координат слова х.
| n | ||||
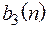
|
Тогда 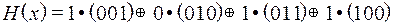 =
= 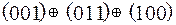 =
=
= 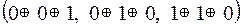 =
= 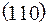 .
.
Кодом Хемминга называется подмножество двоичных слов 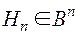 , для каждого из которых функция Хемминга равна нулевому вектору. Таким образом
, для каждого из которых функция Хемминга равна нулевому вектору. Таким образом 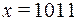
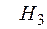 .
.
Утверждение.
Количество двоичных слов 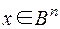 , принадлежащих коду Хемминга равно
, принадлежащих коду Хемминга равно 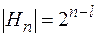 .
.
 2015-04-01
2015-04-01 662
662








