Если функция 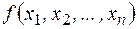 представима единственной элементарной конъюнкцией
представима единственной элементарной конъюнкцией
– всех n переменных, то 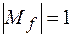 ;
;
– 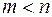 переменных, то
переменных, то 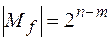 .
.
Пример.
Пусть 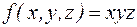 . Она принимает значение 1 тогда и только тогда, когда x = 1, y = 1, z = 1. Значит
. Она принимает значение 1 тогда и только тогда, когда x = 1, y = 1, z = 1. Значит 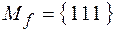 .
.
Пусть 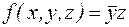 . Она принимает значение 1 тогда и только тогда, когда y = 0, z = 1. Значит, чему равняется переменная х – неважно, и она может принимать любые значения. Поэтому
. Она принимает значение 1 тогда и только тогда, когда y = 0, z = 1. Значит, чему равняется переменная х – неважно, и она может принимать любые значения. Поэтому 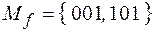 .
.
Утверждение 1. Представление функции в виде ДНФ соответствует представлению ее единичного множества в виде объединения единичных множеств входящих в эту ДНФ элементарных конъюнкций.
Пример. Пусть функция представлена своей ДНФ.
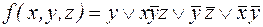 .
.
Тогда ее единичное множество может быть представлено в виде:
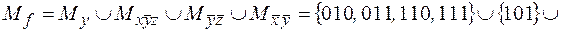
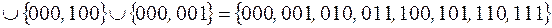 .
.
Получилось, что 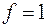 .
.
Утверждение 2. Любая конъюнкция ДНФ функции является импликантом данной функции.
Утверждение 3. Если конъюнкция ДНФ функции не является простым импликантом, то можно найти соответствующий ей простой импликант (импликанты) и заменить им (их дизъюнкцией) непростой импликант.
ДНФ, состоящая только из простых импликантов, называется сокращенной.
Пример. Пусть функция представлена своей ДНФ.
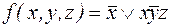 .
.
Тогда ее единичное множество имеет вид:
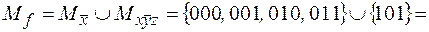
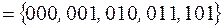 .
.
Очевидно, что 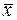 – это простой импликант. Он состоит из одной буквы, и если ее вычеркнуть, получится вырожденная конъюнкция (конъюнкция не имеющая переменных), что возможно только в случае, если
– это простой импликант. Он состоит из одной буквы, и если ее вычеркнуть, получится вырожденная конъюнкция (конъюнкция не имеющая переменных), что возможно только в случае, если 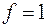 .
.
Проверим, будет ли простым импликант 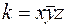 .
.
Вычеркнем из него переменную х. Получим конъюнкцию 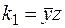 . Ее единичное множество содержит 2 набора:
. Ее единичное множество содержит 2 набора: 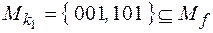 , то есть
, то есть 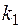 по-прежнему является импликантом f. Значит
по-прежнему является импликантом f. Значит 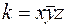 – не простой импликант.
– не простой импликант.
В свою очередь, полученный импликант 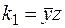 является простым, так как вычеркивать из него буквы нельзя. Нельзя вычеркнуть
является простым, так как вычеркивать из него буквы нельзя. Нельзя вычеркнуть 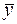 – так как оставшаяся переменная z имеет единичное множество, содержащее 4 вектора с последней 1, а в
– так как оставшаяся переменная z имеет единичное множество, содержащее 4 вектора с последней 1, а в 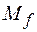 таких векторов только 3; z – так как оставшаяся переменная
таких векторов только 3; z – так как оставшаяся переменная 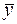 имеет единичное множество, содержащее 4 вектора с 0 на втором месте, а в
имеет единичное множество, содержащее 4 вектора с 0 на втором месте, а в 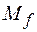 таких векторов только 3.
таких векторов только 3.
Значит, импликант 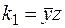 – простой и им можно заменить в ДНФ исходный импликант
– простой и им можно заменить в ДНФ исходный импликант 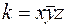 .
.
Вычеркнем из k переменную 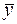 . Получим конъюнкцию
. Получим конъюнкцию 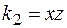 . Ее единичное множество содержит 2 набора:
. Ее единичное множество содержит 2 набора: 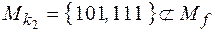 , то есть
, то есть 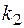 уже не является импликантом f.
уже не является импликантом f.
Вычеркнем из него переменную z. Получим конъюнкцию 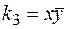 . Ее единичное множество содержит 2 набора:
. Ее единичное множество содержит 2 набора: 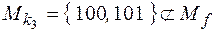 , то есть
, то есть 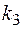 также не является импликантом f.
также не является импликантом f.
Таким образом, ДНФ вида 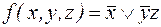 является сокращенной.
является сокращенной.
 2015-04-01
2015-04-01 419
419








