Матрицаның жолдары мен оған көшiрме бағандарының орындарының ауыстыруынан шыққан матрицаны транспандау деп аталады. А матрицаның трансподалған матрицасын А¢ арқылы белгiленедi.
Мысалы. 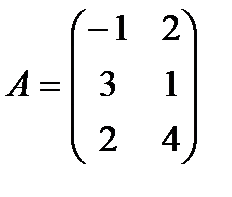 болса,
болса, 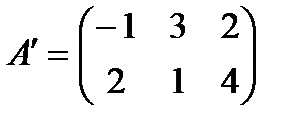 .
.
Тапсырманы орындауға арналған нұсқаулар
ІІ. Матрицаның экономикалық интрперетациясы
5 мысал.
Берілгені: Өнеркәсіпте - төрт түрлі бұйым шығарылады
төрт түрлі бұйымға - төрт түрлі шикізат жұмсалынады
А матрицасы - шикізаттардың жұмсалу нормасының элементтері
шикізат түрлері 1 2 3 4
А = 
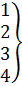 бұйым түрлері
бұйым түрлері
Әрбір бұйым түрінің жоспар бойынша жасалу мөлшері: 50, 45, 30 және 20
Табу керек: әрбір жұмсалатын шикізаттың мөлшерін
Шешімі: Шығатын бұйымдардың векторлық жоспары: 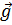 = (50, 45, 30, 20).
= (50, 45, 30, 20).
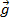 * А = (50, 45, 30, 20)
* А = (50, 45, 30, 20)  =
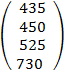
= 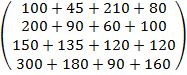 =
= 
6 мысал. Төрт өнімге жұмсалатын төрт түрлі шикізаттың мөлшері алдыңғы мысалда берілген А матрицасымен анықталатын болсын. Егер шикізаттардың өзіндік құндары 8, 6, 5, 4 ал оларды тасымалдауға жұмсалатын шығындар 1, 2, 3, 3 болса, онда а) әрбір өнімге жұмсалатын шикізаттардың шығындарын, оларды тасымалдауға жұмсалатын шығындарды және б) жасалатын бұйымдардың векторлық жоспары 1-2 тапсырмадағыдай болған жағдайда шикізатқа жұмсалатын жалпы шығын мен оларды тасымалдауға жұмсалатын жалпы шығымндарды табыңыз.
Шешімі: Шикізаттардың өзіндік құндары мен тасымалдау шығындарының матрицасын құрамыз:
С = 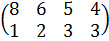
Сонда бірінші сұрақтың жауабы А матрицасы мен СТ матрицасының көбейтіндісі ретінде беріледі:
А* СТ = 
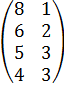 =
= 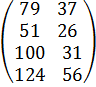
Мұндағы СТ – С матрицасының трансполданған матрицасы. Бұйымдардың векторлық жоспары
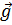 = (50, 45, 30, 20) болған жағдайда шикізаттардың жалпы шығыны және оларды тасымалдау шығыны
= (50, 45, 30, 20) болған жағдайда шикізаттардың жалпы шығыны және оларды тасымалдау шығыны 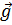 векторы мен АСТ матрицасының көбейтіндісі ретінде беріледі:
векторы мен АСТ матрицасының көбейтіндісі ретінде беріледі:
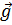 * АСТ = (50, 45, 30, 20)
* АСТ = (50, 45, 30, 20) 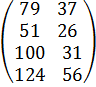 = (11725 5070).
= (11725 5070).
Мысал.
Берілгені: Бес өнеркәсіп – 3 түрлі шикізаттан 4 түрлі бұйым шығарады.
- күндік өнімділіктері
- әрбір өнеркәсіптің әр жыл сайын істейтін күндерінің сандары
- әрбір өнімнің құны.
Табу керек: 1.Әрбір өнеркәсіптің әрбір бұйым бойынша жылдық өнімділігі;
2.Әрбір өнеркәсіптің әрбір шикізатты жылдық жұмсау мөлшері;
3.Әрбір өнеркәсіптің бұйымдарды шығаруға жұмсайтын шикізаттарды сатып алу үшін керек ететін жылдық несие мөлшері.
Керекті өндірістік көрсеткіштер:
| Бұйым түрі | Өнеркәсіп өнімділігі өнім/күн | Шикізаттың жұмсалуы салмақ бірлігі/шикізат | ||||||
| Жылдық жұмыс күндерінің саны | Шикізат құны | |||||||
Шешуі: Өнеркәсіптің барлық экономикалық спектрін сипаттайтын матрицалар:
1) өнеркәсіптің барлық бұйымдар бойынша өнімділік матрицасын құру (А матрицасы - өнеркәсіптің әрбір бұйым бойынша күндік өнімділігі)
- әрбір өнеркәсіптің әрбір бұйым бойынша жылдық өнімділігін ( Ажыл) табу.
2) бір өнімге жұмсалатын шикізаттың (В матрицасы) матрицасын құру
- шикізаттардың түрлері бойынша күндік жұмсалу шығынын табу
- әрбір өнеркәсіптің әрбір шикізатты жылдық жұмсау мөлшерін табу.
3) шикізат бағасының векторын (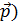 құру
құру
- әрбір өнеркәсіптің бұйымдарды шығаруға жұмсайтын шикізаттарды сатып алу үшін бөлетін жылдық шығыны (P - шикізаттарды сатып алу үшін жұмсалатын өнеркәсіптер несиелерінің мөлшерлері)
Мысал.
Берілгені: Төрт өнімге жұмсалатын төрт түрлі шикізаттың мөлшері - А матрицасы
шикізаттардың өзіндік құндары: 8, 6, 5, 4
тасымалдауға жұмсалатын шығындар: 1, 2, 3, 3
Табу керек:
а) әрбір өнімге жұмсалатын шикізаттардың шығындарын, оларды тасымалдауға жұмсалатын шығындарды
б) шикізатқа жұмсалатын жалпы шығынды
в)тасымалдауға жұмсалатын жалпы шығындарды.
Шешуі:
-шикізаттардың өзіндік құндары мен тасымалдау шығындарының матрицасын (С) құру
- 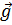 - бұйымдардың векторолық жоспарын құру
- бұйымдардың векторолық жоспарын құру
- шикізаттардың жалпы шығыны және оларды тасымалдау шығынын есептеу.
Өнімділік матрицасы:
өнеркәсіп өнімділігі
А = 
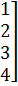 бұйым түрі
бұйым түрі
Әрбір өнеркәсіптің әрбір бұйым бойынша жылдық өнімділігі
Ажыл = 
Бір өнімге жұмсалатын шикізаттың матрицасы:
бұйым түрі
В = 
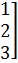 шикізат түрі
шикізат түрі
Күндік жұмсалуы:
ВА = 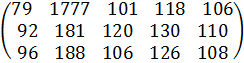
Өнеркәсіптің әрбір шикізатты жылдық жұмсау мөлшері ВА матрицасының көбейтіндісіне тең:
ВАжыл = 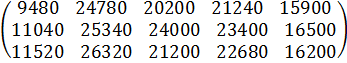
Шикізат бағасының векторын жазамыз: 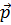 = (50, 30,40).
= (50, 30,40).
Әрбір өнеркәсіптің бұйымдарды шығаруға жұмсайтын жылдық шығыны:
P = 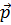 * ВАжыл = (1266000, 3052000, 2578000, 2671200, 1938000)
* ВАжыл = (1266000, 3052000, 2578000, 2671200, 1938000)
Өзіндік жұмыс тапсырмалары
І. Матрицаға қолданылатын амалдар тақырыбына арналған тапсырмалар:
1 Орындау А+(- В), егер
а) А = 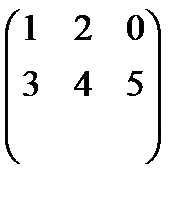 ; В =
; В = 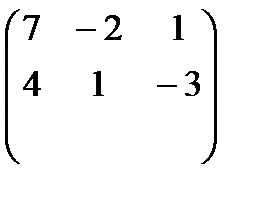 б) А=
б) А= 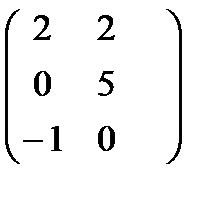 ; В =
; В = 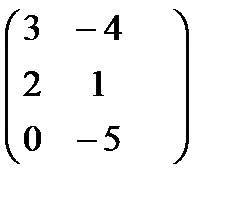
2. Матрицаның сызықтық комбинацияларын тап:
а) 2А+3В, мұндағы 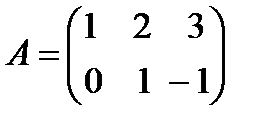 ,
, 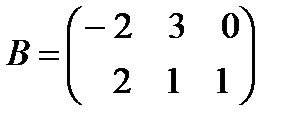 .
.
б) 4А – 5В, мұндағы 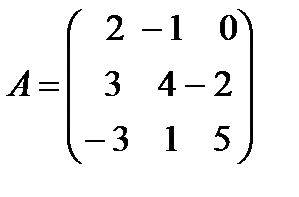 ,
, 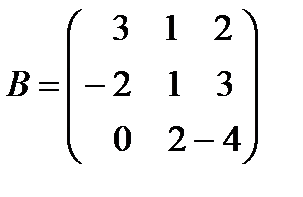 .
.
в) 3А+4В, мұндағы 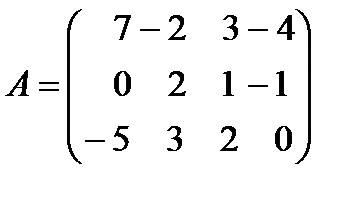 ,
, 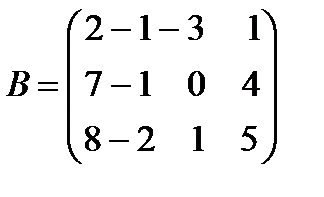 .
.
3. А матрицаны санға көбейту
а) -1,5 А, егер А = 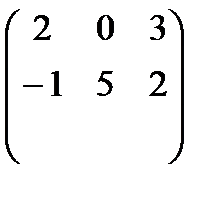 б) 2А, егер А =
б) 2А, егер А = 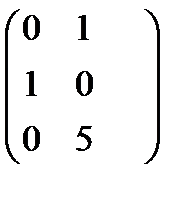
4.Амалды орында
А = 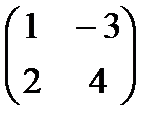 , Е
, Е 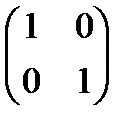
5. А және В матрицасын көбейту, егер
а) А = 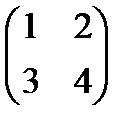 В =
В = 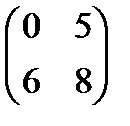 Табу керек: А
Табу керек: А  В және В
В және В  А
А
б) А = 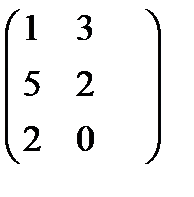 В =
В = 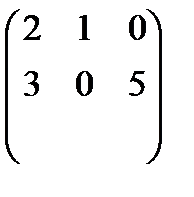 Табу керек: А
Табу керек: А  В және В
В және В  А
А
6.АВ және ВА матрицалардың көбейтіндісін тап (егер мүмкін болса).
а) 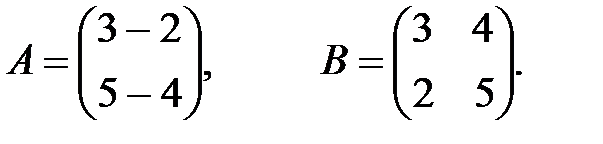 б)
б) 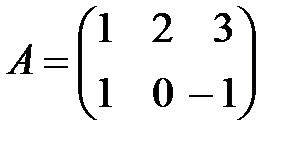 ,
, 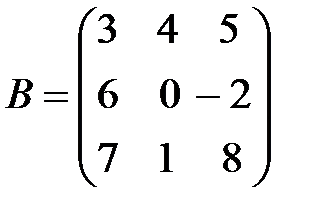 .
.
в) 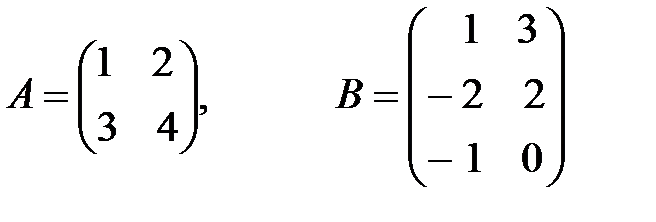 .
.
7. Амалды орында
а) А 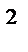 , А
, А 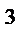 , егер А =
, егер А = 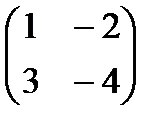 б) С=-5А+2В, егер А=
б) С=-5А+2В, егер А= 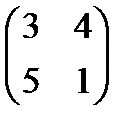 , В =
, В = 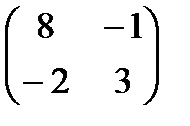
в) С=2 А 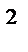 + 5А-3Е, егер А =
+ 5А-3Е, егер А = 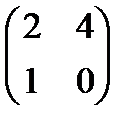 , Е =
, Е = 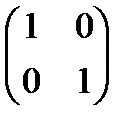
г) 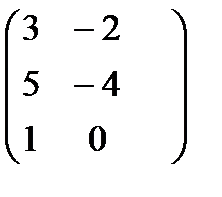

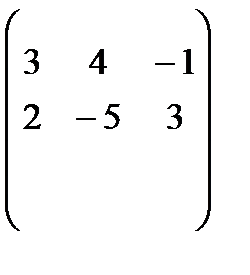
ІІ. Матрицаның экономикалық интерпретациясы тақырыбына арналған тапсырмалар
Берілгені: Pi –дің әрбір өніміне S1, S2, S3 үш түрлі шикізаттардың жұмсалу нормасы S матрицасымен және шығарылатын өнім жоспары P=(p1, p2) матрицасымен берілген; егер С матрицасы - әрбір шикізаттың мөлшері (у.е.) белгілі болған жағдайда, жоспарланған екі түрлі P1 және P2 өнімін шығару үшін шикізаттың жалпы мөлшерін табу.
Төмендегі көрсеткіштерін табу: S – шикізаттың жұмсалуы (х1, х2, х3);
P – өнім түрі; С – өнеркәсіп шығаратын өнім құны.
Шешуі: Сызықтық теңдеулдер жүйесін құру P*S(х)= С
1 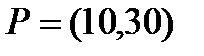 ;
; 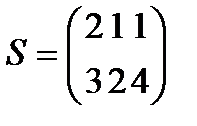 ;
; 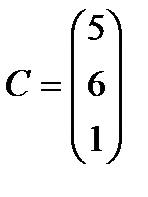 . 2
. 2 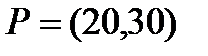 ;
; 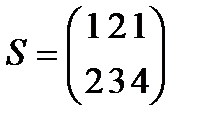 ;
; 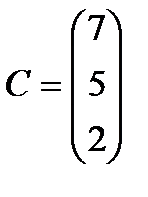 .
.
3 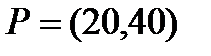 ;
; 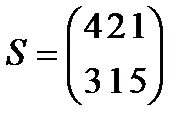 ;
; 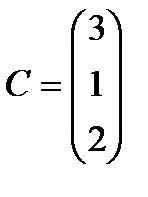 . 4
. 4 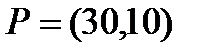 ;
; 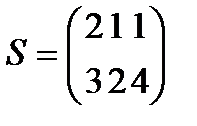 ;
; 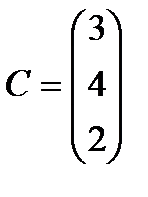 .
.
5 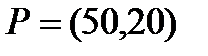 ;
; 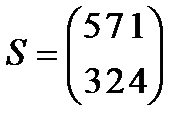 ;
; 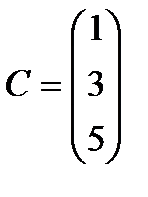 . 6
. 6 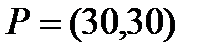 ;
; 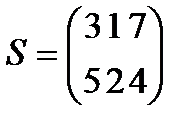 ;
; 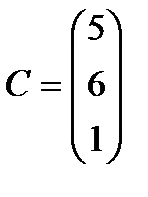 .
.
7 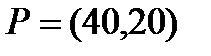 ;
; 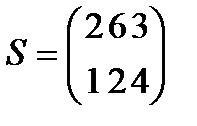 ;
; 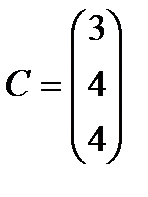 . 8
. 8 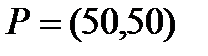 ;
; 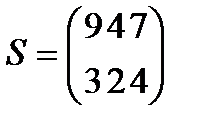 ;
; 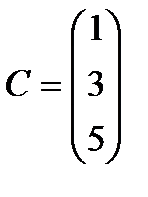 .
.
9 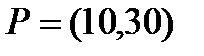 ;
; 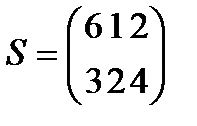 ;
; 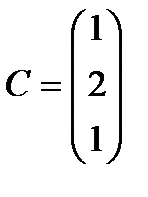 . 10
. 10 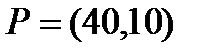 ;
; 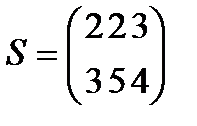 ;
; 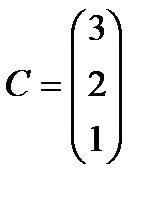 .
.
11 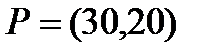 ;
; 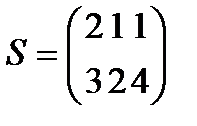 ;
; 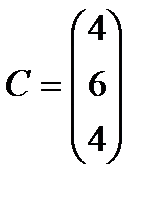 . 12
. 12 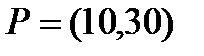 ;
; 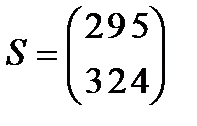 ;
; 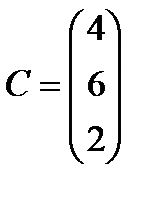 .
.
13 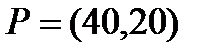 ;
; 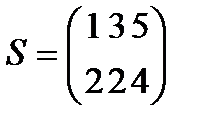 ;
; 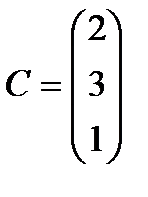 . 14
. 14  ;
; 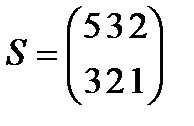 ;
; 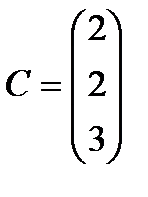 .
.
15 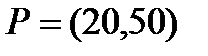 ;
; 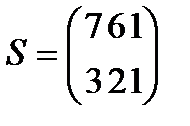 ;
; 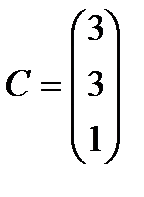 . 16
. 16 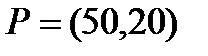 ;
; 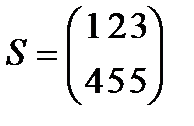 ;
; 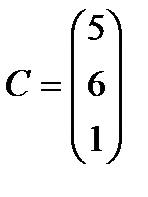 .
.
17 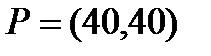 ;
; 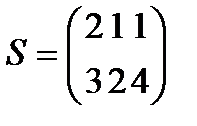 ;
; 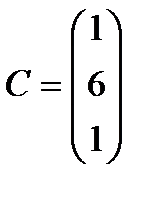 . 18
. 18 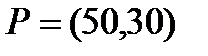 ;
; 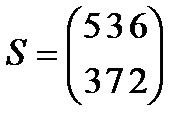 ;
; 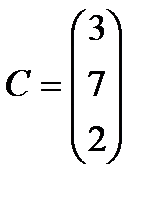 .
.
19 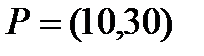 ;
; 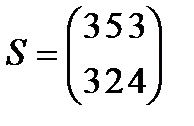 ;
; 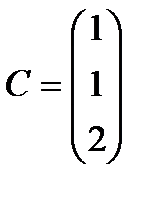 . 20
. 20 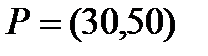 ;
; 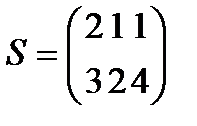 ;
; 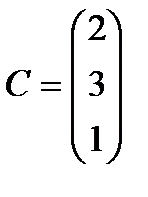 .
.
Практикалық жұмыс №4
«Анықтауышты есептеу тәсілдері»
Жұмыс мақсаты: Анықтауыштың есептеу тәсілдерін есеп шығаруда қолдана білу.
Жұмыс мазмұны
1.Екініші ретті анықтаушы: 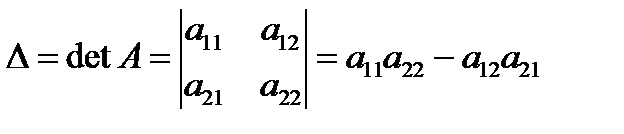
1 мысал. 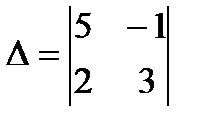 екiншi реттi анықтауыштың мәндерiн табайық.
екiншi реттi анықтауыштың мәндерiн табайық.
Шешуi. 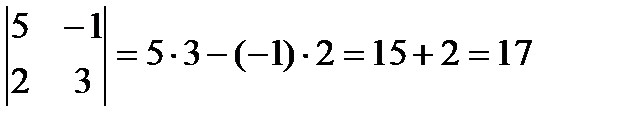
2.Үшінші ретті анықтаушы (Саррюс ережесі):
 =
= 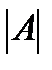 =
= 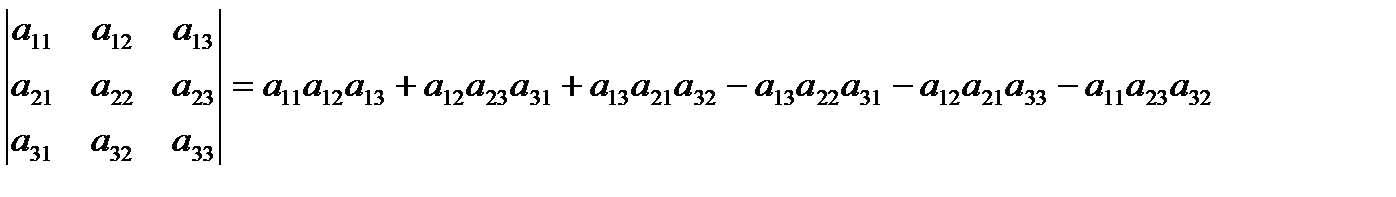 .
.
Үшбұрыш ережесімен есептелінеді
Оң таңбамен «+»:; теріс таңбамен «-»:
негізгі диагональ қосымша диагональ
2 мысал 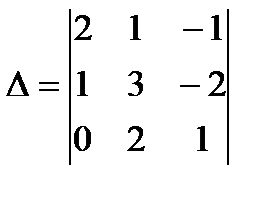 үшiншi реттi анықтауыштың мәнiн табу.
үшiншi реттi анықтауыштың мәнiн табу.
Шешуi: Үшбұрыш ережесімен табу жолы
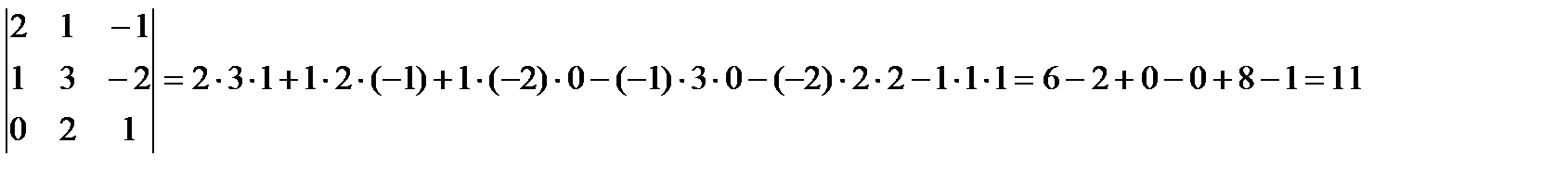 Үшінші ретті анықтауышты есептеудің 2-ші тәсілі
Үшінші ретті анықтауышты есептеудің 2-ші тәсілі
 =
= 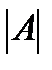 =
= 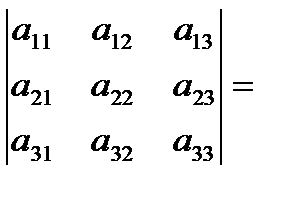
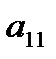
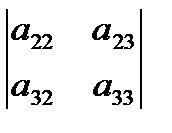 -
- 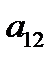
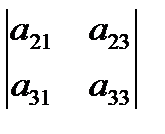 +
+ 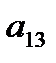
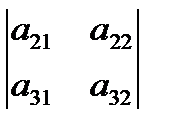
3 мысал. 2 тәсіл.
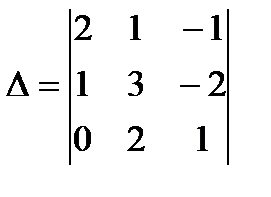 үшiншi реттi анықтауыштың мәнін табу.
үшiншi реттi анықтауыштың мәнін табу.
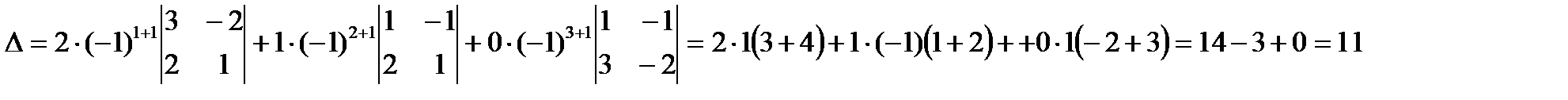
3. n–реттi анықтауыштың aij элементi тұрған i-жол мен j-бағанды сызып тастағаннан қалған (n-1) реттi анықтауышты ол элементтiң миноры деп аталады. Анықтауыштың aij элементтің минорын Mij арқылы белгілейміз.
Үшінші реттi анықтауыштың a21, a33 элементтерiнiң минорлары M21, M33 табу:
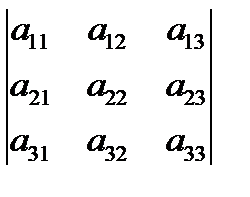 үшінші ретті анықтаушы
үшінші ретті анықтаушы
Шешуі: 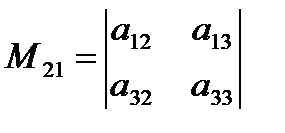 ,
, 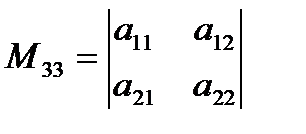
4.Анықтауыштың aij элементінің алгебралық толықтауышы 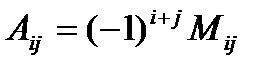
4 мысал: 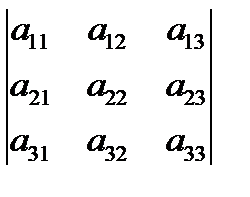 үшінші ретті анықтауштың а21, а33 элементтерінің алгебралық толықтауыштарын табу.
үшінші ретті анықтауштың а21, а33 элементтерінің алгебралық толықтауыштарын табу.
Шешуі:
А21=(-1)2+1M21=(-1)3 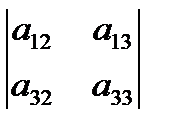 =-
=- 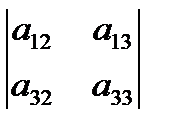 ,
,
A33=(-1)3+3M33=(-1)6 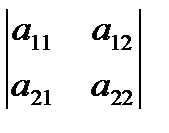 =
= 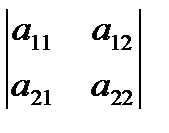
5 мысал. 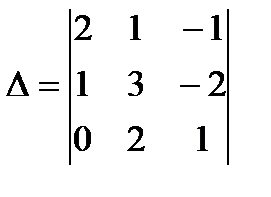
үшiншi реттi анықтауыштың бiрiншi бағанында тұрған элементтердiң миноры мен алгебралық толықтауыштарын табыңдар.
Шешуi. a11=2 тұрған бірінші жол мен бірінші бағанды сызып тастасақ, қалғандары оның миноры болады:
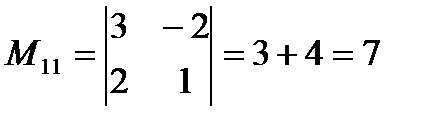 ;
;
Ал, алгебралық толықтауышы:
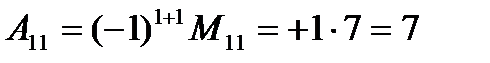
болады. A21=1 тұрған екінші жол мен бірінші бағанды сызып тастаса:
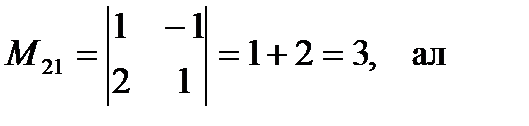
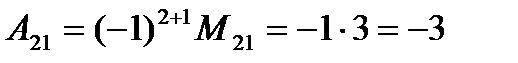 ,
,
M 31= 0 тұрған үшінші жол мен бірінші бағанды сызып тастасақ:
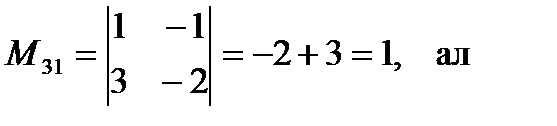
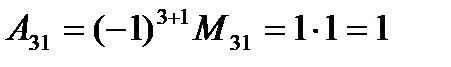
5.Кері матрица тек кана шаршы матрица үшін анықталады. А-1 матрицасы А матрицаға кері матрица деп аталады, егер 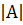 ≠0.
≠0.
А-1 А=АА-1 =Е, мұнда Е- бірлік матрица.
Кері матрица формуласы: 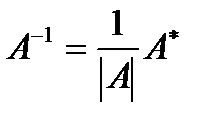 ,
, 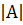 ≠0
≠0
Кері матрицаны табу алгоритмі:
1.Матрица анықтауышын табу 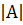 ≠0
≠0
2.Берілген матрица элементтерінің алгебралық толықтауыштарынан (Аij) матрица құру.
3. Матрицаны транспандау және жаңа матрица (А*) алу.
4. Кері матрица формуласын пайдалану.
5.Тексеру: А 
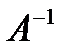 = Е
= Е
Тапсырманы орындауға арналған нұсқаулар
Мысал
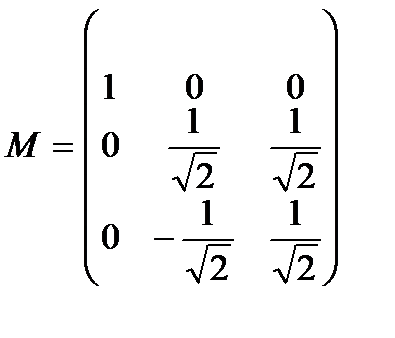 матрицаға керi матрицаны табыңдар.
матрицаға керi матрицаны табыңдар.
Шешуi. 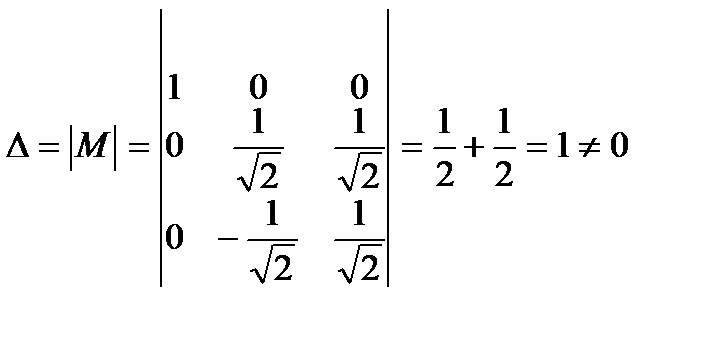
Сондықтан, матрицаның керi матрицасы бар. Элементтердiң алгебралық толықтауыштарын табамыз:
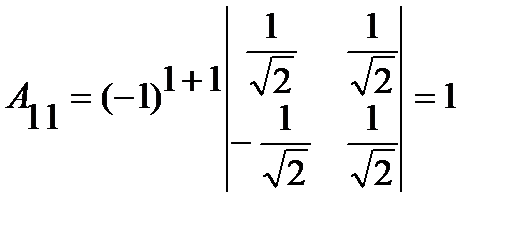 ;
; 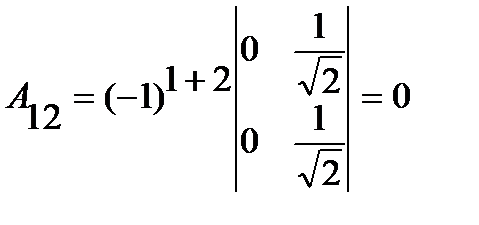
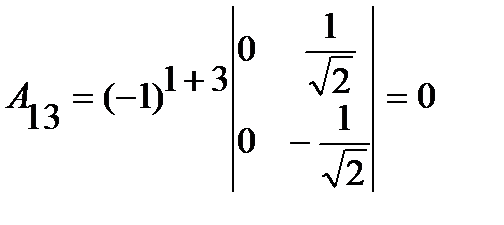 ;
; 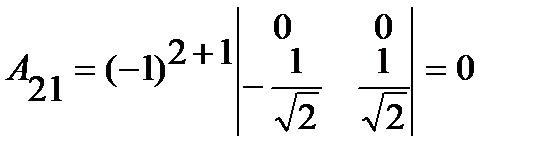
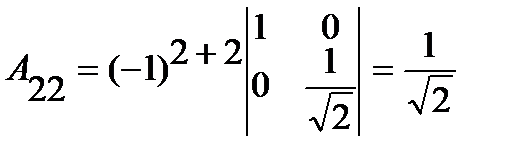 ;
; 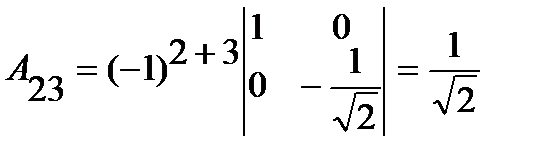
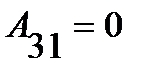 ;
; 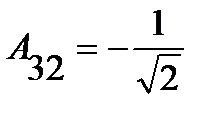 ;
; 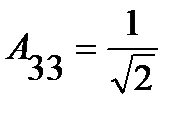 .
.
Сонда: 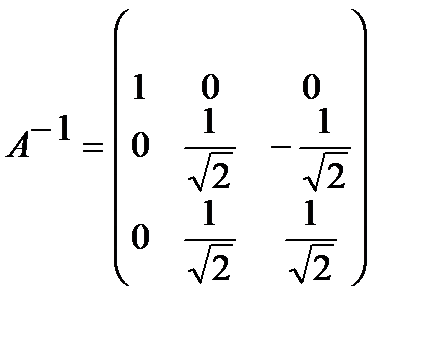
7 мысал. 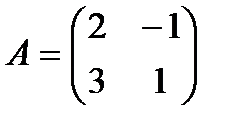 матрицаның керi матрицасын табыңдар.
матрицаның керi матрицасын табыңдар.
Шешуi: Бұл матрицаның анықтауышы: 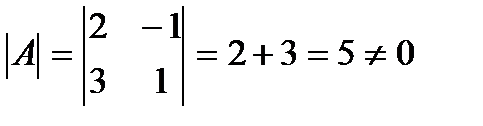 .
.
Сондықтан, матрицаның керi матрицасы болады. Оны табу үшiн оның барлық элементтерiнiң алгебралық толықтауыштарын табамыз:
a11=2 элемент үшiн A11=(-1)1+1=1 a12=2 элемент үшiн A12=3(-1)1+2=-3
a21=2 элемент үшiн A21=-1(-1)2+1=-1 a22=2 элемент үшiн A22=2(-1)2+2=2.
Сонда: 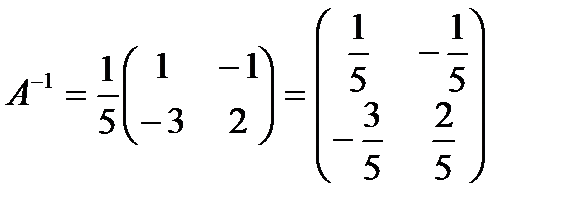 .
.
8 мысал. 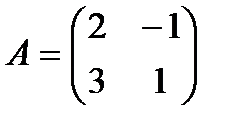 матрицаның керi матрицасын табыңдар.
матрицаның керi матрицасын табыңдар.
Шешуi: Бұл матрицаның анықтауышы: 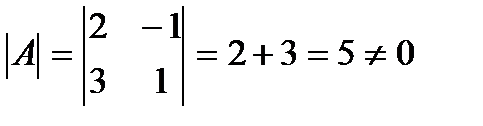 .
.
Сондықтан, матрицаның керi матрицасы болады. Оны табу үшiн оның барлық элементтерiнiң алгебралық толықтауыштарын табамыз:
a11=2 элемент үшiн A11=(-1)1+1=1 a12=2 элемент үшiн A12=3(-1)1+2=-3
a21=2 элемент үшiн A21=-1(-1)2+1=-1 a22=2 элемент үшiн A22=2(-1)2+2=2.
Сонда: 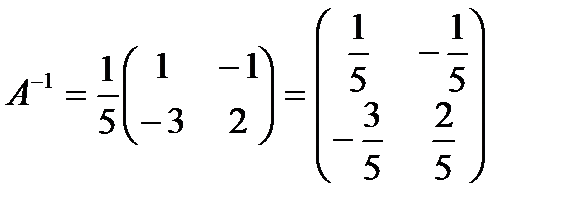 .
.
Өзіндік жұмыс тапсырмалары
І. Анықтауыш тақырыбына арналған тапсырмалар:
1.Екінші ретті анықтауышты есепте:
а) 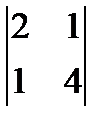 ; б)
; б) 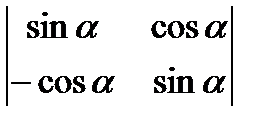 ; в)
; в) 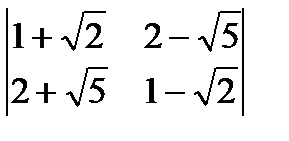 .
.
2.Теңдеуді шеш: 3.Теңсіздікті шеш:
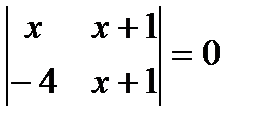 ;
; 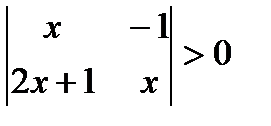 ;
;
4.Екінші ретті анықтаушты есепте.
а) 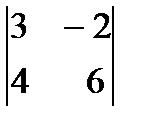 ,б)
,б) 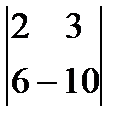 ,в)
,в) 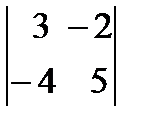 , г)
, г) 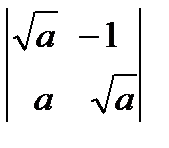 ,д)
,д) 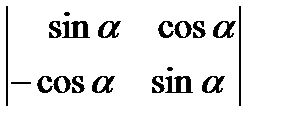
5.Есепте
а) 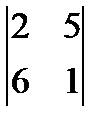 ; б)
; б) 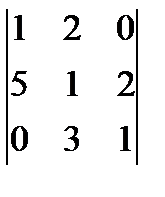 ; в)
; в) 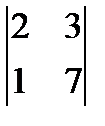 ; г)
; г) 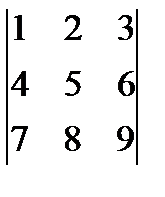 ; д)
; д) 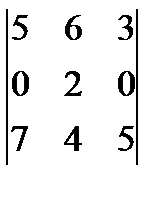
6.Үшінші ретті анықтауышты есепте:
а) 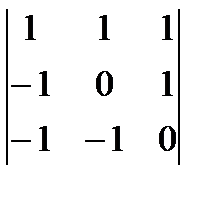 ; б)
; б) 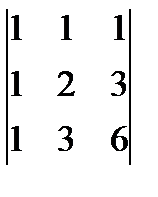 ; в)
; в) 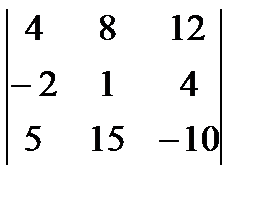 . г)
. г) 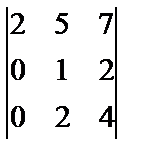 ; д)
; д) 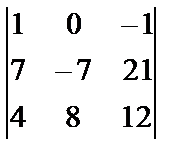 .
.
7.Теңдеуді шеш: 8.Теңсіздікті шеш:
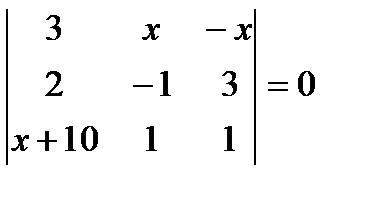 .
. 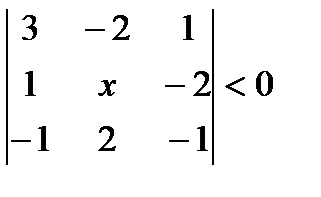 ;
;
9.Үшінші ретті анықтауышты есепте.
а) 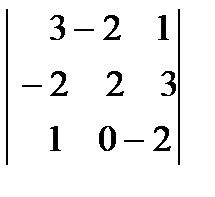 , б)
, б) 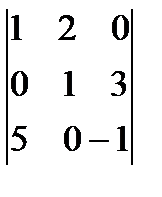 , в)
, в) 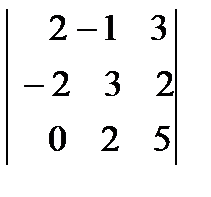 , г)
, г) 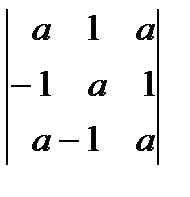
10.Теңдіктің дұрыстығын айқындау:
А деңгейлік тапсырма
1. 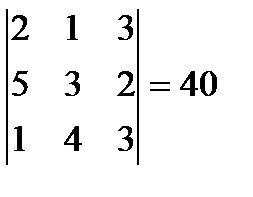 2.
2. 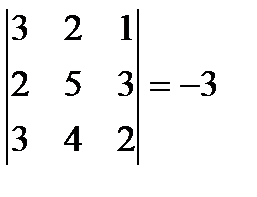 3.
3. 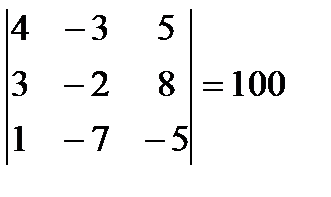
4. 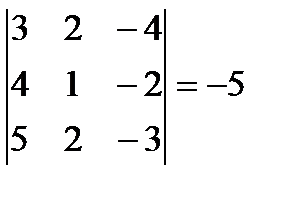 5.
5. 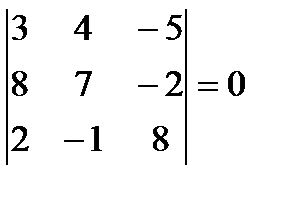 6.
6. 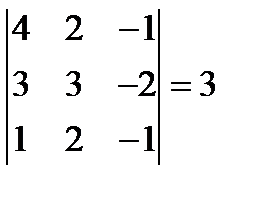
Б деңгейлік тапсырма
7. 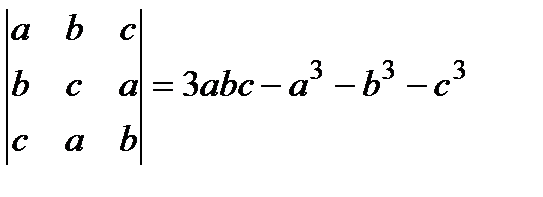 8.
8. 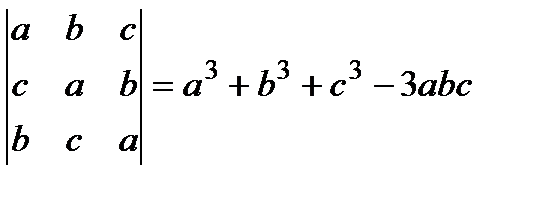
9. 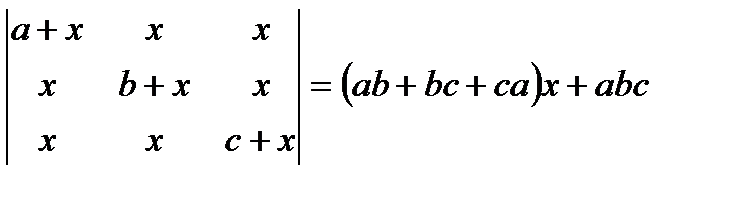 10.
10. 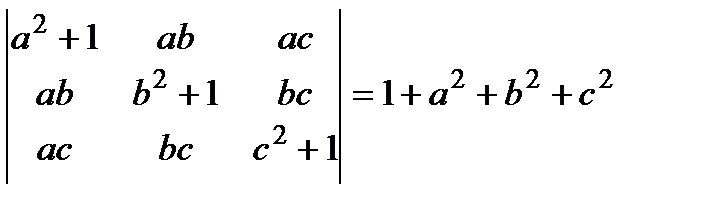
11.Анықтауышты әртүрлі тәсілмен есептеу:
1. 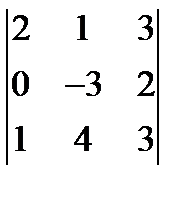 2.
2. 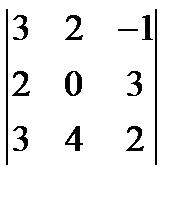 3.
3. 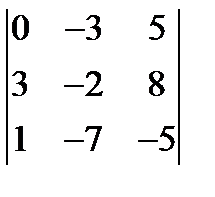
4. 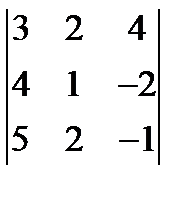 5.
5. 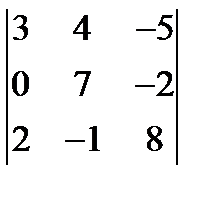 6.
6. 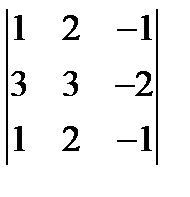
ІІ. Кері матрица тақырыбына арналған тапсырмалар:
1.Табу керек: 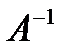 , егер
, егер
а) 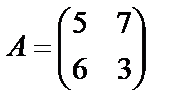 ; б)
; б) 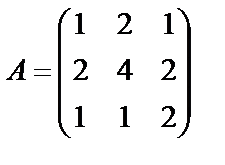 ; в)
; в) 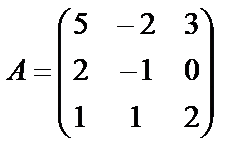 .
.
г) А= 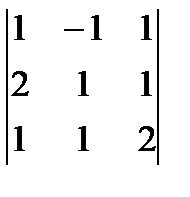 ; д)
; д) 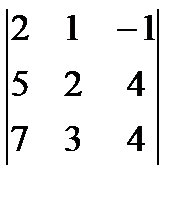 ; е)
; е) 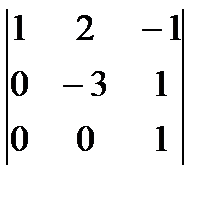
3.Кері матрицаны табу 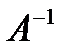 :
:
1. 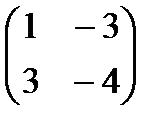 2.
2. 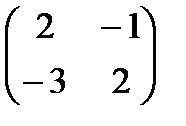 3.
3. 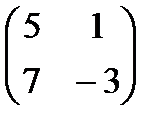 4.
4. 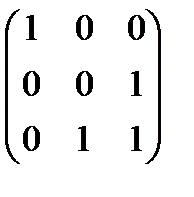
5. 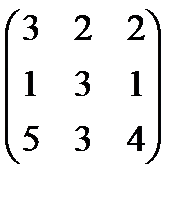 6.
6. 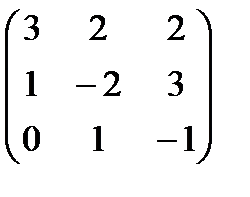 7
7 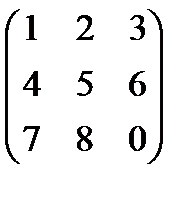 8.
8. 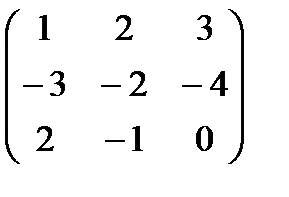
4. Берілген А матрицаның кері матрицасы бар ма, бар болса есепте:
А= 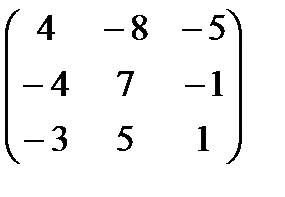
Практикалық жұмыс №5
«Сызықтық теңдеулер жүйесін Гаусс тәсілімен шешу. Крамер формуласы. Матрицалық теңдеу.»
Жұмыс мақсаты:
Сызықтық теңдеулер жүйесін матрицалық (Гаусс, Крамер, кері матрица) тәсілдермен шешуге дағдыландыру.
Жұмыс мазмұны:
Сызықтық теңдеулер жүйесі 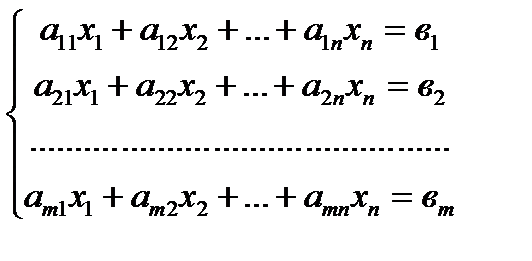
1. Алгебралық сызықтық теңдеулер жүйесін Гаусс тәсілімен шешу екі кезеңнен тұрады.
Бірінші кезең (тура жол тәсілі) – жүйе үшбұрыш түріне келтіріледі.
Екінші кезең (кері жол) – белгісіздер соңғы белгісізден бастап, біріншісіне қарай тізбектеп анықталынады.
Мысалы: Жүйені шешу: 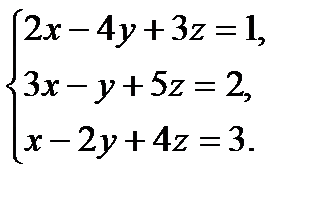
Шешімі: Жүйеден матрицаны алып, оны үшбұрыш түріне келтіреміз:
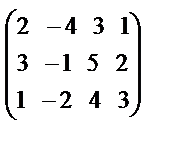 ~
~ 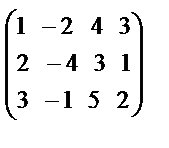 ~
~ 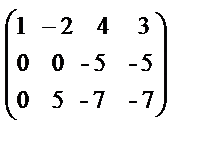 ~
~ 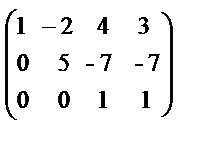
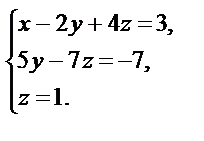
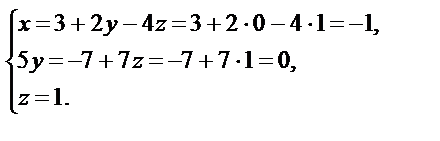 Жауабы: (-1,0,1)
Жауабы: (-1,0,1)
 2015-04-01
2015-04-01 1982
1982








