нерівноточних| вимірів
Наближеними значеннями до стандарту є середня квадратична|з'являються| і емпірична середня квадратична| похибки вимірюваної величини. Вони ж є|з'являються| абсолютними кількісними мірами точності результатів вимірів|вимірів| і їх функцій. При зрівнюванні нерівноточних| вимірів|вимірів| виникає необхідність вводити спеціальну міру точності. Такою мірою є вага, формула обчислення|підрахунку| якої (2.15) наведена в п.п. 2.5. Розглянемо|розглядуватимемо| детально фізичний сенс|зміст| цього поняття.
Вага це спеціальна характеристика відносної точності вимірів і їх функцій, обчислена як величина, обернено пропорційна квадрату стандарта, тобто дисперсії результатів випадкових вимірів.
Якщо існує ряд нерівноточних результатів вимірів l1, l2,…, ln точність яких характеризується стандартами σ1, σ2,…, σn відповідно, то ваги, що характеризують їх відносну точність, визначаються відношеннями
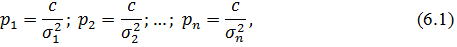
де с – загальний коефіцієнт пропорційності.
Звідси випливає, що вибір с ізрівним квадрату стандарту σi2 деякого результату виміри (реального або уявного) рівнозначний прийняттю ваги цього результату за одиницю.
Позначимо стандарт результату виміру, що має вагу, рівну одиниці символом 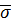 .
.
Тоді рівняння (6.1) можна записати у наступному|слідуючому| вигляді|виді|:
Величину  прийнято називати стандартом одиниці ваги, а його наближені значення відповідно середньою квадратичною похибкою одиниці ваги і емпіричною середньою квадратичною похибкою одиниці ваги.
прийнято називати стандартом одиниці ваги, а його наближені значення відповідно середньою квадратичною похибкою одиниці ваги і емпіричною середньою квадратичною похибкою одиниці ваги.
Як випливає з наведених вище міркувань і виразів (6.1) і (6.2), результати рівноточних вимірів, що мають однакові стандарти, тобто σ1=σ2=…=σn матимуть однакову вагу, яку можна прийняти рівною одиниці p1=p2=…=pn=1.
Очевидно, що результати нерівноточних| вимірів|вимірів|, отримані|одержувати| за різних умов, матимуть нерівні ваги. Визначимо значення простої арифметичної середини L незалежних нерівноточних| результатів вимірів|вимірів|. Для цього зробимо наступні|такі| математичні перетворення. На підставі формальних співвідношень (6.1) запишемо пропорцію

де σ – стандарт окремого виміру; σL – стандарт простої арифметичної середини.
Враховуючи результати обґрунтування другої властивості простої арифметичної середини, а саме формальні перетворення (5.3), можна записати
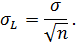
Підставляючи значення σL у пропорцію (6.3), отримаємо

Звідси випливає, що вага арифметичної середини незалежних нерівноточних| результатів вимірів|вимірів| в n разів більше ваги окремого
результату.
Припустивши|передбачати|, що стандарт одиниці ваги дорівнює середній квадратичній| похибці одиниці ваги (див. формулу (6.2)), формула (6.4) набере вигляду

Таким чином, вага арифметичної середини незалежних результатів вимірів одиничної ваги дорівнює кількості цих результатів. При обробці результатів однорідних вимірів їх ваги є безрозмірними величинами. Якщо ж результати вимірів мають різну розмірність, наприклад, довжини лінії виміряні в метрах, а горизонтальні кути в секундах, то вага буде іменованою величиною 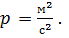
6.2. Вага функцій результатів нерівноточних| вимірів|вимірів|
Для оцінки відносної точності функції незалежних результатів нерівноточних| вимірів|вимірів| скористаємося формулою, яка випливає з|із| доведення основної теореми теорії похибок, а саме формули (4.2)
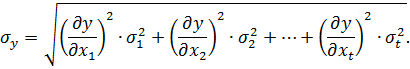
Перетворимо отриману формулу з метою переходу в ній від стандартів σ до вагів р. Для цього піднесемо ліву і праву частину формули (4.2) до квадрату і підставимо замість квадратів стандартів σi2 вирази (6.1) 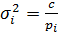 та, скоротивши ліву і праву частини на загальний множник c, отримаємо формальний запис
та, скоротивши ліву і праву частини на загальний множник c, отримаємо формальний запис
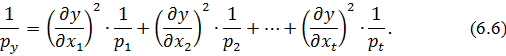
Розглянемо простий окремий випадок використання формули (6.6) для функції з однією змінною y = cx. Підставимо цю формулу до (6.6) і, зробивши відповідні перетворення, отримаємо 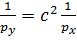 або
або 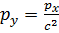 . Застосувавши цю рівність до кожного виміру
. Застосувавши цю рівність до кожного виміру 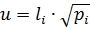 , де li – результат i-го вимірювання, а pi – його вага, отримаємо
, де li – результат i-го вимірювання, а pi – його вага, отримаємо

Отже, з цих математичних побудов випливає, що якщо помножити результат вимірів на корінь квадратний з його ваги, то вага добутку 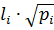 дорівнюватиме одиниці, а його стандарт дорівнюватиме стандарту одиниці ваги
дорівнюватиме одиниці, а його стандарт дорівнюватиме стандарту одиниці ваги 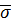 .
.
З пропорції (6.2), отриманої на основі (6.1) запишемо 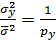 . Перетворюючи цю формулу знайдемо вагу py і стандарт σy функції y=cx,
. Перетворюючи цю формулу знайдемо вагу py і стандарт σy функції y=cx, 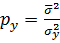

На основі нескладних математичних перетворень отримані|одержувати| формули, які пов'язують вагу функції результатів нерівноточних| вимірів|вимірів| із її точностними| характеристики.
Таким чином, для того, щоб знайти значення стандарту будь-якого результату виміру|виміру| або його функції, достатньо|досить| стандарт одиниці ваги розділити на корінь квадратний |із| ваги цього результату або його функції.
При визначенні ваг на практиці можливі два випадки:
1. Стандарти результатів вимірів|вимірів| відомі або можуть бути визначені теоретично. У цьому випадку для розрахунку вагів використовують вирази (6.1), (6.2) і (6.3).
2. У випадку, якщо|у разі, якщо| стандарти невідомі, то вагам можна дати приблизну оцінку, підставляючи у формулу (6.1) приблизні значення середніх або емпіричних середніх квадратичних| похибок, тобто

Розглянемо|розглядуватимемо| приклади|зразки| математичних побудов|шикувань| для розрахунку вагів у геодезичній практиці.
Приклад 6.1. Математичні перетворення для розрахунку ваги суми кутів теодолітного ходу, виміряних за однакових умов.
Особливістю розв’язання цієї задачі полягає в тому, що вимір кутів теодолітного ходу є рівноточним, тобто їх ваги p1=p2=…=pn=1. Враховуючи цю особливість формула (6.6) набере наступний вигляд
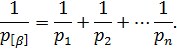
Підставляючи до формули замість 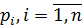 pi, одиничне значення, маємо
pi, одиничне значення, маємо

тобто вага суми кутів|рогів| теодолітного| ходу обернено пропорційна|пропорціональна| кількості виміряних|виміряти| кутів|рогів| цього ходу.
Приклад 6.2. Математичні перетворення для розрахунку ваги лінійних вимірів полігонометричного (теодолітного) ходу. Графічна інтерпретація лінійних вимірів теодолітного ходу ілюструється рис. 6.1.
| L |
| pL |
| p3 |
| p2 |
| p1 |
| dn |
| d3 |
| d2 |
| d1 |
Рис. 6.1 – Ілюстрація до прикладу 6.2
У основу математичних перетворень для розрахунку ваги лінійних вимірів полігонометричного |вимірі| ходу покладений відомий в геодезії факт, що довжина ходу дорівнює сумі довжин його сторін. Цей факт математично можна записати у вигляді рівняння
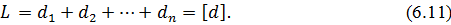
Крім того, відомо, що стандарт довжини лінії за відсутності систематичних похибок пропорційний|пропорціональний| кореню квадратному від|із| довжини лінії
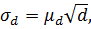
де μd – коефіцієнт випадкового впливу.
Тоді підставляючи до виразів (6.2) σd для кожної лінії отримаємо формули для обчислення ваги виміряних ліній
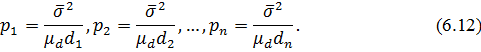
В отриманих|одержувати| виразах виділимо постійну величину і позначимо її
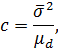
тоді на підставі|основі| (6.3) і з урахуванням|з врахуванням| виразів (6.11) і (6.12) отримаємо
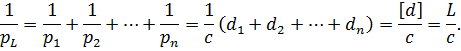
Спростивши отриманий|одержувати| вираз|вираження|, маємо

Таким чином, вага лінійного виміру|вимірів| полігонометричного| ходу обернено пропорційна|пропорціональна| довжині ходу.
Приклад 6.3. Математичні перетворення для розрахунку ваги перевищення нівелірного ходу, прокладеного на рівнинній місцевості.
Якщо хід прокладений на рівнинній місцевості при середній відстані між рейками 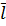 кількість станцій в ході буде дорівнювати
кількість станцій в ході буде дорівнювати 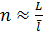 .
.
Враховуючи формулу (6.6) запишемо
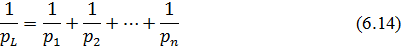
де p1, p2,…, pn=1 – ваги виміряних перевищень на станції. Беручи до уваги, що на всіх станціях перевищення виміряні в однакових умовах (рівноточно), тобто p1=p2=…=pn=p вираз (6.14) можна представити у вигляді
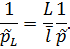
Позначивши 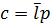 отримаємо
отримаємо 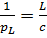 звідки випливає
звідки випливає

Слід відзначити|помітити| рівність формул (6.13) і (6.15), тобто вага перевищення нівелірного|нівелір| ходу, прокладеного на рівнинній місцевості так само|місцевий|, як і за вимірів|вимірах| полігометричного| ходу (див. приклад|зразок| 6.2), обернено пропорційна|пропорціональний| довжині ходу.
Аналогічно|за аналогією| можна довести, що вага перевищення нівелірного|нівелір| ходу, прокладеного на пересіченій місцевості|місцевий|, обернено пропорційна|пропорціональна| кількості станцій, тобто

Таким чином, розглянуті|розглядувати| особливості математичних перетворень, що забезпечують оцінку відносної точності функції незалежних результатів нерівноточних| вимірів|вимірів|, а також приклади|зразки| математичних побудов|шикувань|, що дозволяють розраховувати ваги функціональних залежностей, отриманих|одержувати| з|із| геодезичної практики.
6.3. Загальна|спільна| арифметична середина і її властивості
Якщо l1, l2,…, ln – незалежні результати вимірів однієї і тієї ж величини Х, відносна точність яких характеризується відповідно вагами p1, p2,…, pn (вимірювання нерівноточні) то за якнайкраще наближені до величини Х приймають загальну арифметичну середину
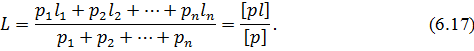
Величину L часто називають середньою зваженою.
Отриману|одержувати| формулу (6.17) можна застосовувати лише тоді, коли окремі результати вимірів можливо порівнювати|вимірів| і вони мають величини одного порядку|ладу|. Не можна усереднювати результати, отримані|одержувати| за умов вимірів|вимірів|, що суттєво відрізняться, наприклад, не можна усереднювати довжину лінії, виміряну|виміряти| один раз звичайною|звичною| рулеткою, а другий раз світлодальноміром|, або величину кута|рогу|, виміряного|виміряти| один раз технічним теодолітом, а другий раз високоточним теодолітом. Виходячи з вищевикладеного випливає, що на ваги у формулі (6.17) мають бути накладені обмежувальні умови, які можна виразити|виказувати| нерівністю

де c1, c2 – деякі позитивні постійні.
За аналогією з математичними побудовами|шикуваннями| виконаними|проробити| в п.п.5.1 розглянемо|розглядуватимемо| основні властивості загальної|спільної| арифметичної середини незалежних нерівноточних| результатів вимірів|вимірів|.
Властивості загальної|спільної| арифметичної середини
Властивість 1. Вага загальної арифметичної середини незалежних нерівнаточних результатів вимірів дорівнює сумі вагів цих вимірів.
Для математичного обґрунтування цього твердження представимо |затвердження| формулу (6.17) |уявлятимемо| у вигляді
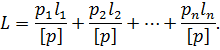
Розглядаючи L як функцію незалежних змінних l1, l2,…, ln для визначення її ваги, знайдемо частинні похідні
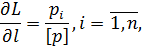
і підставимо їх до формули (6.6). У результаті отримаємо|одержуватимемо| наступне|слідуюче| співвідношення
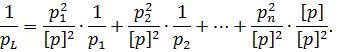
Після|потім| скорочень і перетворення отриманої|одержувати| формули, маємо

що формально демонструє вірність|вмісту| властивості 1. Відповідно стандарт загальної|спільної| арифметичної середини, враховуючи формулу (6.8), буде рівний

Властивість 2. Якщо загальна арифметична середина отримане з результатів вимірів, вільних від систематичних похибок, то і сама вона не містить систематичної похибки.
Ця властивість, аналогічно третій властивості простої арифметичної середини, яка розглядалася|розглядувало| для ряду рівноточних|лави| вимірів|вимірів| в п.п.5.1. Тому справедливим є запис
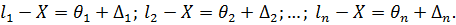
Помноживши кожну з цих рівностей на відповідну вагу 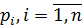 , та склавши почленно і розділивши на [ p ] отримаємо
, та склавши почленно і розділивши на [ p ] отримаємо
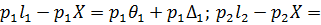
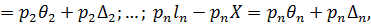
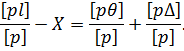
Права частина отриманої рівності складається з двох частин, які відповідають систематичній і випадковій похибкам загальної арифметичної середини. Звідси витікає, що якщо θ1=θ2=…=θn дорівнює нулю, то і [ pθ ] дорівнюватиме нулю, що і доводить сформульовану вище властивість.
Властивість 3. Якщо результати нерівноточних вимірів вільні від систематичних похибок, то їх загальна арифметична середина при збільшенні кількості вимірів наближається до істинного значення вимірюваної величини.
За аналогією з першою властивістю простої арифметичної середини для ряду рівноточних|лави| | результатів вимірів|вимірів| запишемо

На підставі обмежувальних умов на вимірювання (6.18) запишемо наступні нерівності c1<p1; c1<p2;…; c1<pn. Підсумуємо праві і ліві їх частини і отримаємо нову нерівність 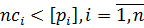 . Звідки можна зробити висновок, що за n→∞ має місце границя
. Звідки можна зробити висновок, що за n→∞ має місце границя

З отриманого виразу (6.22) і формули (6.20) виходить, що стандарт σL наближатиметься до нуля, тобто при n→∞

Це означає, що загальна|спільна| арифметична середина L наближатиметься до постійної величини, а оскільки|тому що| постійна величина не може містити|утримувати| систематичної похибки, то вона має дорівнювати вимірюваній величині Х.
На підставі третьої і другої властивості можна зробити висновок|укладення|, що за відсутності систематичних похибок загальна|спільна| арифметична середина L є|з'являється| спроможною і незміщеною оцінкою Х.
Властивість 4. Сума добутків відхилень результатів вимірів від загальної арифметичної середини

на відповідні їх ваги дорівнює нулю|нуль-індикатору|, тобто

Помножимо почленно кожний вираз із системи рівнянь (6.24) на відповідні ваги 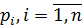 і, підсумувавши отриману|одержувати| у такий спосіб|в такий спосіб| рівність, матимемо
і, підсумувавши отриману|одержувати| у такий спосіб|в такий спосіб| рівність, матимемо
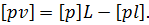
Враховуючи формулу для знаходження загальної арифметичної середини (6.17) 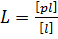 підставляючи її до отриманого виразу і перетворюючи, матимемо
підставляючи її до отриманого виразу і перетворюючи, матимемо
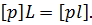
Підставляючи до отриманої формули вираз (6.25) отримаємо 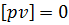 , що і потрібно було довести.
, що і потрібно було довести.
Залишається обґрунтувати, що з|із| усіх можливих функцій, отриманих|одержувати| в результаті нерівноточних|унаслідок|| вимірів|вимірів| цю властивіст має тільки|лише| загальне|спільна| арифметичне середнє. Для цього візьмемо відмінну від (6.24) деяку функцію у |біля| і запишемо для неї систему рівнянь:

Віднімаючи від|із| формули (6.26) вираз|вираження| (6.24), отримаємо|одержуватимемо| різницю відхилень
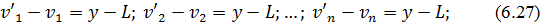
Помножимо кожну з рівностей на відповідні ваги 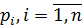 , а потім підсумуємо почленно і отримаємо формулу
, а потім підсумуємо почленно і отримаємо формулу 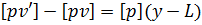 , яку, враховуючи (6.25), можна перетворити на співвідношення вигляду
, яку, враховуючи (6.25), можна перетворити на співвідношення вигляду 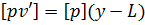 . Звідси витікає, що
. Звідси витікає, що 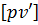 буде дорівнювати нулю, тоді і тільки тоді, коли y=L що і потрібно було довести.
буде дорівнювати нулю, тоді і тільки тоді, коли y=L що і потрібно було довести.
Властивість 5. Сума добутків ваг на квадрати відхилень від загальної арифметичної середини завжди менша суми добутків ваг на квадрати
відхилень від будь-якої іншої функції тих же результатів вимірів, тобто

що відповідає нерівності

Для доказу отриманої|одержувати| нерівності перетворимо формулу (6.27) до вигляду
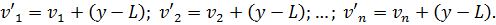 |виду|
|виду|
Піднесемо ліві і праві частини|частки| цієї рівності до квадрату і, привівши їх у відповідність з|із| формулами скороченого множення для многочленів, отримаємо|одержуватимемо|:
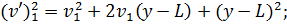
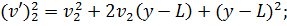
…
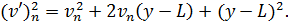
Потім помножимо ліві і праві частини отриманих рівнянь на відповідні ваги 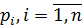 , отримані вирази почлено складемо. У результаті отримаємо формулу
, отримані вирази почлено складемо. У результаті отримаємо формулу 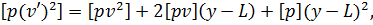 яка з урахуванням рівності (6.25) набере вигляду
яка з урахуванням рівності (6.25) набере вигляду 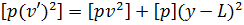 . Звідки випливає очевидна нерівність (6.29), що і підтверджує справедливість формулювання п'ятої властивості загальної арифметичної середини результатів нерівноточных вимірів.
. Звідки випливає очевидна нерівність (6.29), що і підтверджує справедливість формулювання п'ятої властивості загальної арифметичної середини результатів нерівноточных вимірів.
Таким чином, враховуючи окремі математичні формули|шикування| знаходження простої арифметичної середини для рівноточних| вимірів|вимірів|, розглянуті|розглядувати| властивості загальної|спільної| арифметичної середини однієї з основних характеристик оцінювання точності нерівноточних| геодезичних вимірів|вимірів|.
Знання властивостей загальної|спільної| арифметичної середини дозволяє правильно і коректно організувати математичні обчислення|підрахунки| в процесі обробки нерівноточних| геодезичних вимірів|вимірів|.
6.4. Формула емпіричної середньої квадратичної| похибки
 2015-04-01
2015-04-01 1536
1536







