Бесциркуляционное обтекание круглого цилиндра

Продолжим рассмотрение метода наложения потоков. Полученное в примере 6.5 течение, называемое диполем, на первый взгляд носит достаточно абстрактный характер. Однако, как будет показано ниже, такая точка зрения не совсем справедлива. Используя понятие диполя, можно получить весьма интересные и полезные для практических приложений результаты. Для подтверждения этого проанализируем течение, возникающее при наложении прямолинейного поступательного потока на диполь с центром, расположенным в начале координат. Прямолинейный поток движется вдоль оси Ox со скоростью, равной единице, т.е. 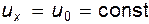; 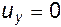. Потенциал скорости

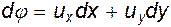
и 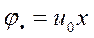с точностью до произвольной постоянной.

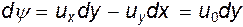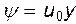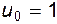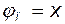Функция тока и . Если, как принято в условии, , то и 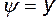. Примем для упрощения выкладок момент диполя 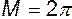, тогда 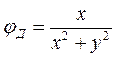и 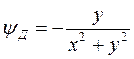. Складывая потенциалы и функции тока, получаем 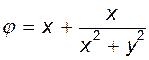и .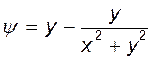

Найдем линии тока, для чего приравняем функцию тока постоянной: 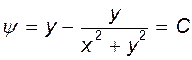, откуда

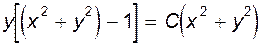(6.33)

Из чего следует, что линии тока течения представляют семейство кривых третьего порядка. Найдем нулевую линию тока, т.е. линию, для которой 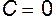. Это дает два уравнения:

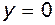и ,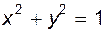

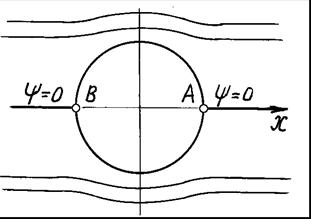т.е. линия тока представляет собой ось x -ов и окружность единичного радиуса с центром в начале координат (см. рис. 6.12). Это позволяет рассматривать окружность как твердую границу и течение вне ее, что приводит к задаче обтекания бесконечно длинного цилиндра.

Покажем, что на достаточно большом удалении от цилиндра скорость направлена вдоль оси x и равна 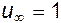. Найдем проекции скоросте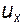й и .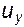

Имеем: ,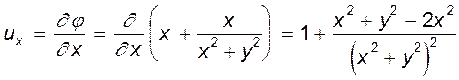

Откуда ;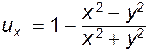

аналогично .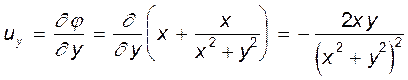

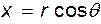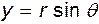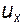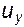Для дальнейшего удобно перейти к полярным координатам, имея в виду, что и . Подстановка этих значений в выражения для и дает:

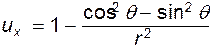(6.34)

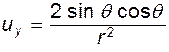(6.35)

Перейдем к пределу. При 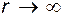получаем 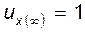и 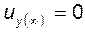, т.е. то, что и требовалось доказать.

Точки B и A, показанные на рис. 6.12, являются так называе­мыми особыми либо критическими точками, т.к. скорость в них обра­щается в нуль. Покажем, что это действительно так, для чего запишем выражение для потенциала скорости в полярных координатах:

;

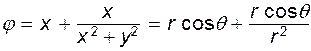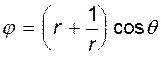(6.36)

Найдем проекции скорости в произвольной точке на произвольной линии тока (рис. 6.13). Имеем:

;

.

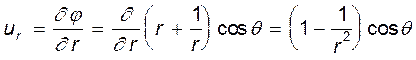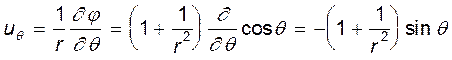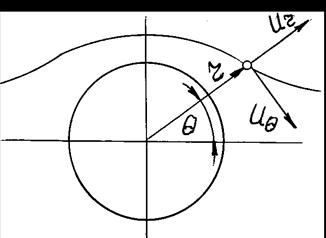На поверхности цилинд­ра 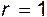и 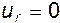, т.е. обтекание безотрывно. Компонента 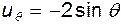. В общем случае, когда ,

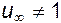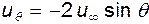(6.37)

Знак «минус» указывает на то, что направление скорости на верхней половине цилиндра противоположно положительному направлению отсчета угла 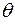. В точках B и A (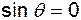) скорости равны нулю, т.е. действительно эти точки являются критическими.