Выпуклости функций

В тех случаях, когда рассматриваемая функция является дифференцируемой на заданном множестве, выяснение вопроса о ее выпуклости может быть осуществлено с помощью дифференциальных критериев выпуклости. Напомним, что функция дифференцируема в точке 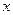, если ее приращение в этой точке может быть записано в виде:

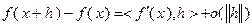(3.2.1)

и дважды дифференцируема в точке 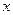, если

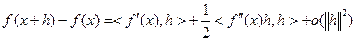(3.2.2)

Теорема 3.2.1

Пусть функция дифференцируема на открытом выпуклом множестве . В этом случае функция выпукла на тогда и только тогда, когда 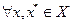выполнено неравенство

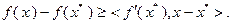(3.2.3)

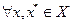Доказательство. Пусть функция выпукла на , т.е. и 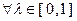выполнено неравенство

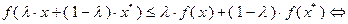
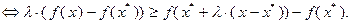(3.2.4)

Из неравенства (3.2.4) следует:

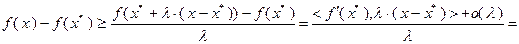
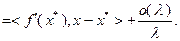
Поскольку 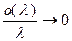при 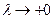, неравенство (3.2.3) будет выполнено.

Теперь рассмотрим доказательство в обратную сторону. 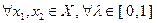определим точку 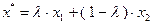. Предположим, что выполнены неравенства:

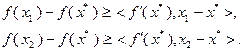
Умножив левую и правую части первого из этих неравенств на 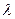, второго – на 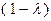, затем сложив их, получим:

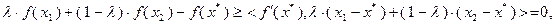
так как 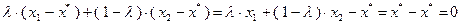. Поэтому

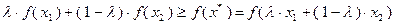, т.е. функция выпукла на множестве . Теорема доказана.

Доказанную теорему можно уточнить для случаев строгой и сильной выпуклости функции . Приведем формулировки соответствующих теорем.

Теорема 3.2.1а

Пусть функция дифференцируема на открытом выпуклом множестве . В этом случае функция строго выпукла на тогда и только тогда, когда 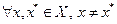выполнено неравенство

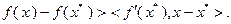
Теорема 3.2.1б

Пусть функция дифференцируема на открытом выпуклом множестве . В этом случае функция сильно выпукла на с константой 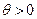тогда и только тогда, когда 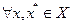выполнено неравенство

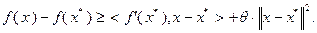
Выполнению условий теоремы 3.2.1 в одномерном случае соответствует расположение графика функции при 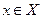целиком выше касательной к нему, проведенной в любой точке с абсциссой, принадлежащей множеству .

Дальнейшее изложение дифференциальных критериев выпуклости функций требует напоминания некоторых определений.

Квадратная матрица 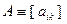называется симметрической, если 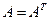( 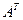– транспонированная матрица), т.е. если .

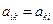Вещественная симметрическая матрица 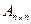называется неотрицательно определенной (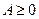), если 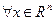выполнено неравенство .

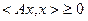Вещественная симметрическая матрица 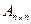называется положительно определенной (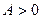), если 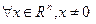выполнено неравенство .

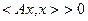Вещественная симметрическая матрица 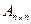называется сильно положительно определенной, если 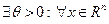выполнено неравенство .

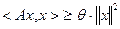В соответствии с критерием Сильвестра вещественная симметрическая матрица является неотрицательно определенной тогда и только тогда, когда все ее главные миноры неотрицательны, и является положительно определенной тогда и только тогда, когда все ее угловые миноры положительны.

Определитель 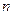-го порядка 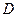матрицы 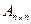имеет 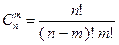главных миноров 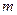-го порядка, диагональные элементы которых являются и диагональными элементами 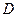. Угловой минор 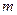-го порядка – это главный минор, который состоит из элементов определителя 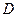, находящихся одновременно в 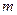его первых строках и 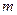первых столбцах.

Например, матрица 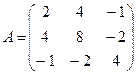имеет следующие главные миноры: 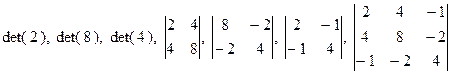и следующие угловые миноры: .

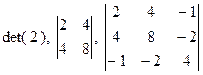Теорема 3.2.2

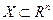Пусть функция дважды непрерывно дифференцируема на открытом выпуклом множестве . В этом случае функция выпукла на тогда и только тогда, когда 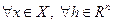выполнено неравенство 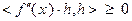, т.е. матрица Гессе неотрицательно определена.

Доказательство. Пусть функция выпукла на множестве . Выберем произвольно точку 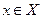и 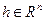. В силу открытости множества при достаточно малых значениях 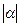имеем 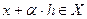. В соответствии с (3.2.2) запишем:

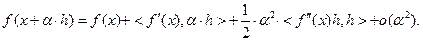(3.2.5)

Из (3.2.5) и теоремы 3.2.1 следует:

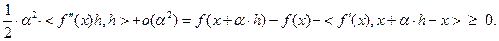
Поэтому

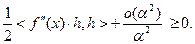
При 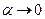имеем 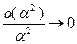и, следовательно, .

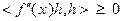Теперь рассмотрим доказательство в обратную сторону. Пусть 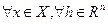выполнено неравенство 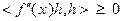. Выберем произвольно точки 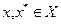и введем обозначение: 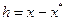. Используя вариант формулы (3.2.2), соответствующий представлению остаточного члена формулы Тейлора в форме Лагранжа, запишем:

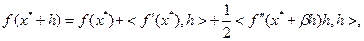(3.2.6)

где 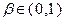и 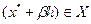в силу выпуклости множества . Из выражения (3.2.6) следует:

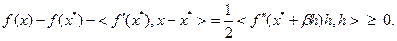
В соответствии с теоремой 3.2.1 функция выпукла на . Теорема доказана.

Для случаев строгой и сильной выпуклости функции соответствующие теоремы формулируются следующим образом.

Теорема 3.2.2а

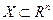Пусть функция дважды непрерывно дифференцируема на открытом выпуклом множестве . В этом случае функция строго выпукла на тогда и только тогда, когда 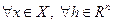выполнено неравенство 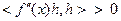, т.е. матрица Гессе положительно определена.

Теорема 3.2.2б

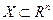Пусть функция дважды непрерывно дифференцируема на открытом выпуклом множестве . В этом случае функция сильно выпукла на с константой 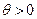тогда и только тогда, когда 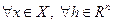выполнено неравенство .

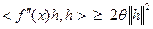Например, для функции одной переменной 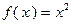имеем:

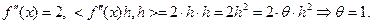
Таким образом, функция 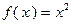является сильно выпуклой на 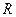с константой .

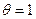Пример 3.2.1. Является ли выпуклой функция

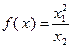на множестве ?

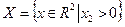Матрица Гессе для заданной функции имеет вид:

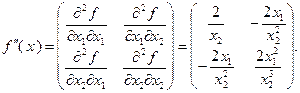
Чтобы выяснить, является ли полученная матрица Гессе неотрицательно определенной, воспользуемся критерием Сильвестра. Для этого найдем главные миноры определителя матрицы Гессе (называемого гессианом) и установим, все ли они неотрицательны. Рассматриваемая матрица имеет три главных минора:

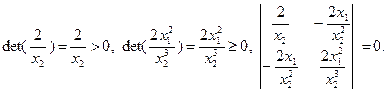
Поскольку все главные миноры неотрицательны, матрица Гессе неотрицательно определена, и в соответствии с теоремой 3.2.2 заданная функция является выпуклой на .

В случае, если функция имеет вид

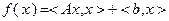, (3.2.7)

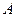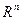где – симметрическая матрица, то выпукла на тогда и только тогда, когда матрица 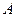неотрицательно определена (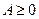) и сильно выпукла на 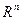тогда и только тогда, когда матрица 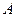положительно определена (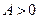). Это следует из того, что для функции (3.2.7) 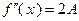и из теорем 3.2.2, 3.2.2б.

Помимо рассмотренных, существуют и другие способы выяснения выпуклости функций. Один из них связан с понятием множества Лебега. Если функция определена на множестве , то множеством Лебега называется множество

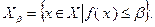
Соответствующая теорема формулируется следующим образом.

Теорема 3.2.3

Если функция сильно выпукла на выпуклом множестве , то все ее множества Лебега на ограничены.

Рис. 3.2.1 иллюстрирует ограниченность множества Лебега 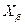сильно выпуклой функции в одномерном случае.

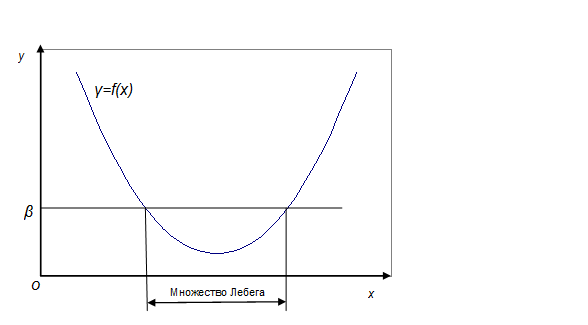
Рис. 3.2.1. Множество Лебега 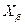для функции