Общая задача оптимизации

Общая задача оптимизации может быть сформулирована в виде:

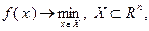(3.3.1)

где – выпуклое множество. В соответствии с теоремой Вейерштрасса, если является замкнутым ограниченным множеством, а функция непрерывна на этом множестве, то она достигает на своих максимального и минимального значений. Замкнутое ограниченное множество называется компактом. Если множество в (3.3.1) не является компактом, но функция сильно выпукла на , то в соответствии с теоремой Вейерштрасса и теоремой 3.2.3, функция достигает на своего минимального значения. Для решения задачи (3.3.1) важное значение имеют следующие теоремы.

Теорема 3.3.1

Если функция непрерывна и выпукла на выпуклом компакте , то множество решений

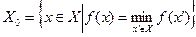
также выпукло.

Доказательство. Введем обозначение:

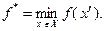
Требуется доказать, что 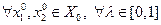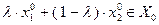. Поскольку функция выпукла на , , 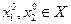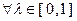выполнено неравенство

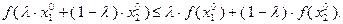
Правая часть этого неравенства равна 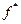, так как 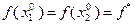. Следовательно, в точке 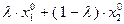достигается минимум функции , т.е. эта точка принадлежит множеству 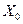. Из полученного результата следует вывод о том, что множество решений 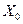является выпуклым множеством. Теорема доказана.

Теорема 3.3.2

Если функция непрерывна и строго выпукла на выпуклом компакте , то множество решений

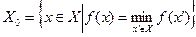
состоит из единственной точки 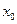, т.е. 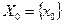. Иначе говоря, строго выпуклая функция достигает минимума в единственной точке.

Доказательство. Доказательство проведем способом от противного. Допустим, что существуют точки 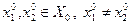. Поскольку строго выпуклая функция является выпуклой функцией, на нее распространяется доказанная выше теорема 3.3.1. В силу этого обстоятельства множество решений 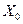является выпуклым. Тогда можно записать:

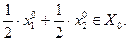(3.3.2)

Так как функция строго выпукла на , справедливо неравенство

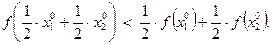(3.3.3)

Используя обозначение 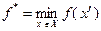, с учетом (3.3.2) для левой части неравенства (3.3.3) можно записать:

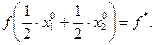
Поскольку 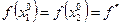, получаем, что правая часть неравенства (3.3.3) также равна 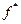. Таким образом, в отношении справедливости неравенства (3.3.3) имеет место противоречие. Следовательно, предположение о том, что множество решений 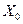состоит более чем из одной точки, является неверным. Теорема доказана.

Точка 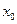называется глобальным решением задачи (3.3.1), если 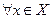выполнено неравенство .

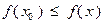Точка 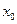называется локальным решением задачи (3.3.1), если 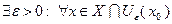выполнено неравенство 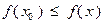. Здесь 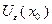является шаром радиуса 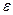с центром в точке .

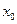Напомним, что шаром радиуса 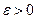с центром в точке 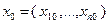называется множество точек 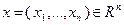, для которых выполнено неравенство:

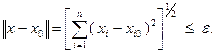
Теорема 3.3.3

Пусть функция выпукла на выпуклом множестве . Тогда всякое локальное решение задачи (3.3.1) является глобальным.

Доказательство. Пусть точка 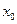является локальным решением задачи (3.3.1). Тогда 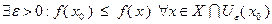, где 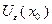– шар радиуса 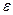с центром в точке 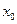. Выберем произвольно точку 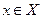и определим точку 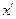в ви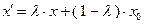де , где 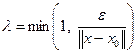. Поскольку множество выпукло, 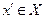. Из выражения для 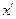следует: 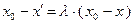. Используя это соотношение, а также выражение для величины 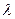, получим:

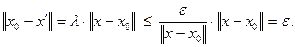(3.3.4)

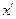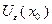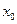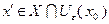Из (3.3.4) следует, что точка принадлежит шару (т.е. находится в окрестности точки ) и с учетом ее принадлежности множеству можно записать: . Следовательно, выполнено неравенство

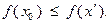(3.3.5)

Учитывая выпуклость функции на множестве , запишем:

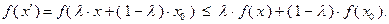
Из этого выражения и неравенства (3.3.5) следует:

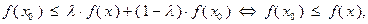
а это означает, что точка 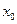является глобальным решением задачи (3.3.1). Теорема доказана.

Задачи оптимизации, в которых всякое локальное решение является глобальным, относят к так называемым унимодальным задачам и рассматривают в выпуклом программировании – разделе математического программирования, изучающем задачи минимизации, в которых минимизируемая функция выпукла, а ограничения заданы также выпуклыми функциями. Задачи такого типа встречаются в математической экономике, теории электрических цепей; к ним относятся также задачи аппроксимации функций.

Если задача оптимизации сформулирована в виде

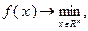(3.3.6)

то она представляет собой задачу безусловной оптимизации. В этом случае необходимым условием существования экстремума в точке 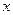является равенство нулю градиента функции в этой точке: 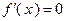(или ).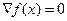

Теорема 3.3.4

Пусть функция дифференцируема на выпуклом множестве и пусть точка 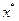– локальное решение задачи (3.3.1). Тогда справедливы следующие заключения:

1) 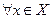выполнено неравенство ;

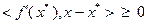2) если функция выпукла на и в точке 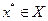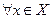выполнено неравенство 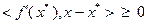, то точка 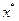является глобальным решением задачи (3.3.1).

Приведенные во 2-м пункте условия являются достаточными условиями существования глобального решения 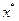задачи (3.3.1).

Доказательство. 1). Поскольку точка 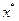является локальным решением задачи (3.3.1), 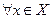при достаточно малых 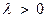выполнено неравенство 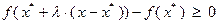. Ясно, что 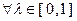имеем 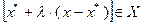в силу выпуклости множества . Используя условие дифференцируемости функции , запишем:

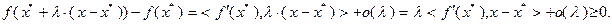
После деления на 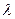(полагаем 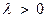) полученное неравенство примет вид:

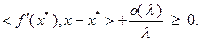
Поскольку 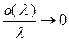при 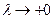, неравенство 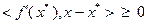будет выполнено.

2). В соответствии с дифференциальным критерием выпуклости (3.2.3) и результатом, полученным в 1-м пункте теоремы, 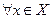имеем:

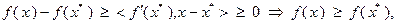
т.е. 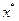– глобальное решение задачи (3.3.1). Теорема доказана.

Лемма 3.3.1

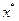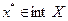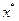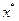Пусть точка находится внутри множества , т.е. , что означает, что имеется некоторая окрестность точки , целиком содержащаяся в множестве вместе с точкой , и пусть для дифференцируемой на функции 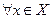выполнено неравенство 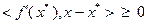. Тогда .

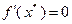Доказательство. В соответствии с условием леммы 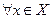имеем 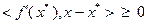, шар 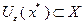. Воспользуемся методом доказательства от противного. Предположим, что 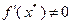, тогда 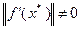. Введем в рассмотрение точку 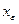, которую определим следующим образом:

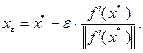(3.3.7)

Тогда для нормы 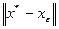из (3.3.7) получим:

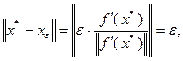
откуда следует, что 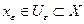. Следовательно, точка 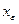должна удовлетворять неравенству 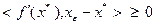, которое в соответствии с (3.3.7) может быть записано в виде:

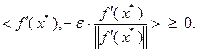
Поскольку скалярное произведение в левой части этого неравенства равно 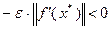, пришли к противоречию. Значит, предположение о том, что 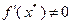, было неверным. Таким образом, 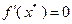. Лемма доказана.

Лемма 3.3.2

Пусть множество является 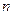-мерным параллелепипедом, т.е.

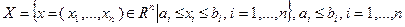(3.3.8)

и пусть на этом множестве заданы дифференцируемая функция и точка 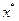– локальное решение задачи (3.3.1). Тогда заключение, приведенное в п.1 теоремы 3.3.4, а именно: 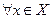выполнено неравенство 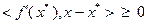, эквивалентно следующему:

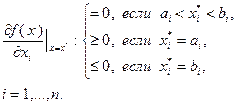
Доказательство. Прежде всего отметим, что множество , заданное в соответствии с (3.3.8), является выпуклым. Учитывая это обстоятельство, а также условия леммы, приходим к выводу, что в данном случае справедливо заключение теоремы 3.3.4, на которое указано в формулировке леммы. Поскольку

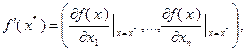
вышеупомянутое заключение теоремы 3.3.4 можно записать в виде: 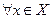выполнено неравенство

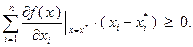(3.3.9)

Выделив из суммы в (3.3.9) 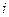-е слагаемое, получим:

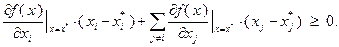(3.3.10)

Поскольку полученное неравенство должно выполняться 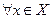, то оно должно иметь место и при 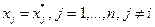. В этом случае (3.3.10) принимает вид:

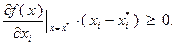(3.3.11)

Если выполнено условие 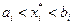, то выражение 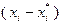принимает положительные, отрицательные значения, а также значение, равное нулю. Поэтому для выполнения неравенства (3.3.11) в любом из этих случаев необходимо и достаточно, чтобы значение производной в (3.3.11) было равно нулю:

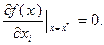
Если 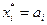, то 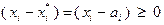и, следовательно, для выполнения (3.3.11) необходимо и достаточно, чтобы значение производной в (3.3.11) было неотрицательным, т.е. должно соблюдаться условие

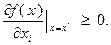
Если 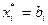, то 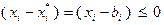и неравенство (3.3.11) будет выполнено тогда и только тогда, когда будет иметь место соотношение

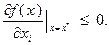
Лемма доказана.

Следствие. Если множество в условии леммы 3.3.2 представляет собой неотрицательный ортант пространства 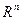, т.е.

,

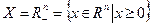то в этом случае из доказанной леммы следует, что заключение «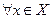 выполнено неравенство 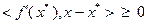» эквивалентно следующему:

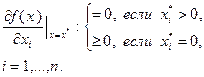
Пример 3.3.1

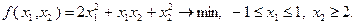
Анализ условия задачи показывает, что множество 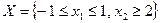является выпуклым, а функция 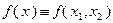может быть представлена в ви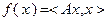де: , где

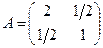– симметрическая положительно определенная матрица, 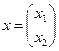. Следовательно, в соответствии с замечаниями к формуле (3.2.7), функция является сильно выпуклой на . На основании изложенного в начале данного раздела и теоремы 3.3.2 (с учетом того, что сильно выпуклая функция является также строго выпуклой) приходим к заключению о том, что в рассматриваемой задаче функция достигает минимума в единственной точке.

В соответствии с леммой 3.3.2 находим:

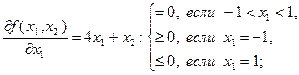(3.3.12)

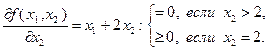(3.3.13)

Комбинируя варианты образования соотношений для частных производных, представленные в (3.3.12) и (3.3.13), по одному из каждой группы, получаем шесть систем, из которых лишь одна окажется совместной в силу существования минимума в единственной точке:

1)

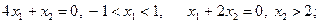
2)

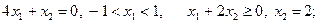
3)

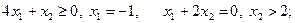
4)

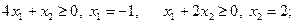
5)

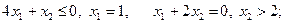
6)

Решая первую систему, получаем:

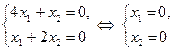– не удовлетворяет условию 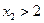. Следовательно, первая система несовместна.

Рассмотрим вторую систему:

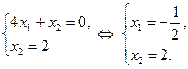
Найденное решение системы уравнений удовлетворяет неравенствам второй системы. Следовательно, точка 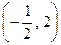есть решение задачи. Все оставшиеся нерассмотренными системы несовместны.