Пример 4.3. Рассмотрим применение информационных технологий Excel для решения транспортной задачи на примере, представленном в таблице 4.2.
Таблица 4.2. Исходные данные для транспортной задачи
| Поставщики | Потребители | Запас | |||
| 1 | 2 | 3 | 4 | ||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| Спрос |
Введем данные в компьютер в виде, показанном на рис. 4.13.
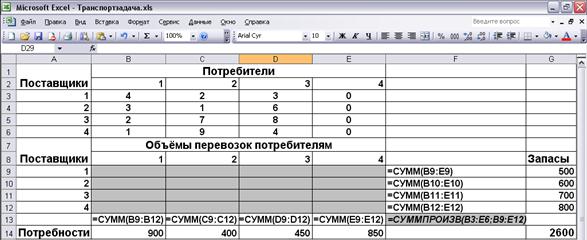
Рис. 4.13. Рабочий лист транспортной задачи 4.4
В массив В3:Е6 введены значения стоимости перевозок единицы груза. В ячейки В14:Е14 введены величины спроса потребителей, в G9:G12 - запасов поставщиков, а в ячейку G14 – суммарного запаса, равного суммарному спросу и составляющего 2600 единиц. Массив В9:Е12 отведен под значения неизвестных 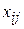 (объемы перевозок), где i =1,2,3,4; j =1,2,3,4. Функция =СУММПРОИЗВ(В3:Е6;В9:Е12) введена в ячейку F13. Функция отражает сумму произведений стоимости
(объемы перевозок), где i =1,2,3,4; j =1,2,3,4. Функция =СУММПРОИЗВ(В3:Е6;В9:Е12) введена в ячейку F13. Функция отражает сумму произведений стоимости 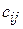 на объемы перевозок
на объемы перевозок 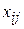 . В массивы F9:F12 и В13:Е13 введены левые части ограничений задачи
. В массивы F9:F12 и В13:Е13 введены левые части ограничений задачи 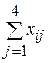 (i =1,2,3,4) и
(i =1,2,3,4) и 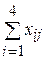 (j =1,2,3,4) соответственно. Эти суммы и целевая функция введены с помощью Мастера функций.
(j =1,2,3,4) соответственно. Эти суммы и целевая функция введены с помощью Мастера функций.
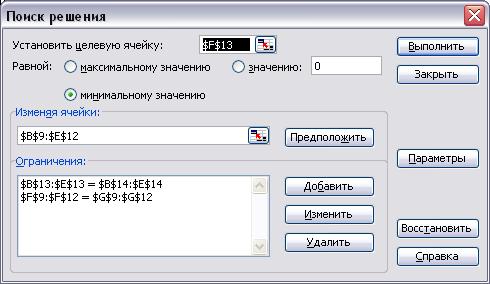
Рис.4.14. Диалоговое окно Поиск решения
После ввода данных вызывается диалоговое окно Поиск решения. В этом диалоговом окне заносится номер ячейки с целевой функцией (F13), номера изменяемых ячеек (В9:Е12), устанавливается направление оптимизации, а также вводятся ограничения (рис. 4.14):
$B$13:$E$13=$B$14:$E$14, $F$9:$F$12=$G$9:$G$12.
В диалоговом окне Параметры поиска решения установим флажок Линейная модель, Неотрицательные значения (рис. 4.6) и, щелкнув по кнопке ОК, возвратимся в диалоговое окно Поиск решения. Щелкнув левой кнопкой мыши по кнопке Выполнить в этом окне, получим на экране результат решения задачи (рис. 4.15).
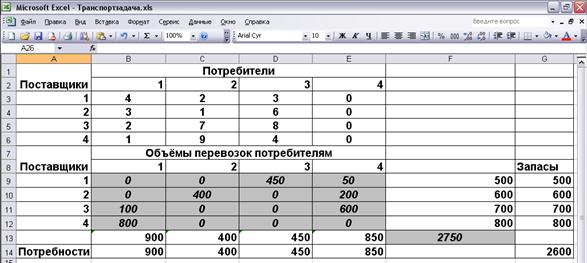
Рис. 4.15. Оптимальное решение транспортной задачи 4.3
Таким образом, 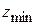 =2750,
=2750, 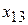 =450,
=450, 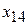 =50,
=50, 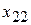 =400,
=400, 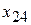 =200,
=200, 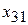 =100,
=100, 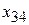 =600,
=600, 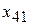 =800. Остальные объемы перевозок груза равны нулю.
=800. Остальные объемы перевозок груза равны нулю.
 2015-04-01
2015-04-01 501
501








