А2. Минимальное число несчастных случаев, достаточное для достоверного анализа травматизма

Известно, что на каждой шахте, в производственном объединении по добыче угля, отрасли в целом число несчастных случаев ото дня ко дню изменяется совершенно незакономерно.

В теории вероятности есть общие решения, направленные на определение такого объема выборки, который обеспечивает минимальную величину ошибки. Но в ветви горной науки, относящейся к охране труда и требующей первоочередного решения, находятся, например, задачи определенного общего числа н/с, необходимого для достоверной оценки изменения их числа в течение года, отдельных месяцев, или изменения травматизма по определенному опасному производственному фактору в какой-либо ограниченный период времени и т.п. Конкретных численных решений для названных и им подобных задач пока нет, поэтому предлагается следующий методический прием решения задач названного типа.

На первом этапе подсчитывается общий, подземный травматизм за последние 10 лет и сравнивается между собой травматизм за первые и вторые 5 лет. Если он различается не более чем на 10%, в дальнейшем все расчеты ведутся для последнего периода времени. Теперь для каждого из пяти последних лет рассчитываются ежемесячные отклонения от среднегодового числа н/с - DХ, %.

Точность измерений в горном деле различными специалистами без каких-либо строгих обоснований принимается самая разная: от 15 до 25-30%. Считаем вполне допустимым при решении задач, относящихся к безопасности труда, выбрать – остановиться на 20% точности определений.

Сначала расчеты выполняются для ежемесячных отклонений от среднегодовых и устанавливается для каждого года максимальное (±) отклонение, 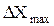, %. Затем такие же расчеты производятся для отклонений средних двух и трехмесячных значений от среднегодовых и таких же отклонений от среднегодового их числа за 2,3 – 5 лет. Тот период времени. Для которого отклонение числа н/с от среднегодового не превышало 20%, принимается за базовый. Он понимается как период времени, в течение которого произошло такое число н/с, которое может рассматриваться как достаточное, 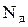, для надёжного (представительного) анализа изменений травматизма по конкретной задаче. Из сказанного следует, что за методическую основу решения задачи принят период времени, но только потому, что он позволяет переходить к численному значению, основанному на количестве н/с, происходящих ежемесячно в годовые отрезки времени.

В теории вероятностей при оценке численности собственно случайной выборки (И.Г. Венецкий, Г.С. Кильдышев. Теория вероятностей и математическая статистика. – М.: Статистка 1975. – 264 с.) считают возможным использование величины коэффициента вариации, рассчитываемого по формуле

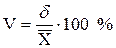, (4.А3)

где 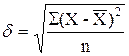и n - число измерений.

Если V < 10%, то это указывает на слабую колеблемость признака, от 10 до 20% - на значительную колеблемость и выше 20% - на сильную колеблемость. Учитывая фактическую высокую изменчивость число н/с на шахтах, при обосновании их числа, необходимого для достоверного анализа, одновременно с расчетом максимальных отклонений оценивали по (4.А2) величины коэффициентов вариации.

Понятно, что предпочтительными являются случаи, когда V £ 10%. Но следует учитывать реальность фактов двух разновидностей. Во-первых, весьма существенный разброс данных, даже если рассматривать месячные изменения числа н/с. Во-вторых, значительную колеблемость фактических (экспериментальных) данных по теории вероятностей, который характеризуется широким диапазоном изменения коэффициентов вариации: 10 – 20%. Если ограничиться диапазоном 10 – 15%, можно рассчитывать на вполне приемлемую колеблемость, находящуюся между слабой и значительной.

Результаты расчетов, выполненных для шахты «Восход» ПО «Снежноеантрацит», доказывают методическую обоснованность подхода к решению обсуждаемой задачи по двум положениям.

1. Хорошо подтверждается справедливость одного из основных положений теории вероятностей, заключающееся в том, что увеличение объема случайной статистической выборки приводит к увеличению ее надежности – представительности. Средний коэффициент вариации максимальных отклонений от среднегодовых в выборках по 3 месяца за 5 лет (28,2%) по сравнению с выборками по одному месяцу за эти же годы (67,8%) уменьшился в 2,4 раза.

2. Для четырех лет из пяти 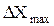при трехмесячной выборке не превосходил 20%. Среднемесячное значение н/с пятилетнего периода времени для этой выборки изменялось от 6,3 до 11,1 в среднем составило 8,2 и вполне может быть округлено до 8,0.

Учитывая то положение, что средняя статистическая величина всегда является наиболее надежной из всей совокупности, она и принимается в качестве базисной.

В дальнейшем те же величины рассчитывались для средних значений н/с за 1,2 и 3 месяца за 2 года (1998-1997 г.г.), три года (1998-1996 г.г.)…пять лет (1998-1994 г.г.). Среднемесячное значение н/с изменялось от 7,2 до 8,4, в среднем составило 7,8, т.е. вновь те же самые 8,0.

Средние абсолютные значения величин коэффициентной вариации максимальных отклонений от среднегодовых в выборках по 1,2 и 3 месяца уменьшились примерно в 1,5 раза и при этом подтвердилась уже обнаруженная тенденция уменьшения коэф. вариации при увеличении выборки от 1 мес. (44,5%) до трех месяцев (17,9%), т.е. вновь уменьшение весьма существенное: в 2,5 раза.

При выборках, соответствующих трехмесячным, округлению н/с за 4 года соответствовал уже V = 13,0%, а за пятилетний суммарный период времени всего V = 6,7%.

По изложенной методике был рассмотрен травматизм за последние 5 лет на всех шахтах ПО «Снежноеантрацит»: «Восход», «Заря», «Миусская», «Северная», «Снежнянская» и «Ударник».

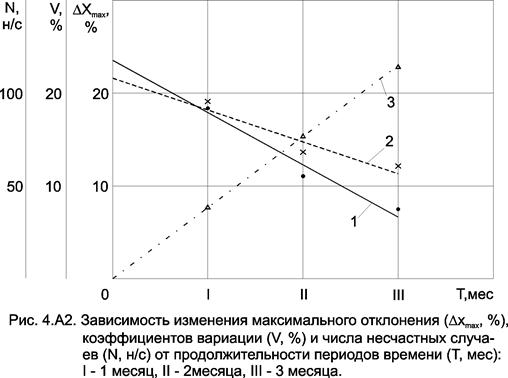
Анализ результатов расчетов приводит к заключению, что при рассмотрении месячных выборок в двух случаях из пяти имело место 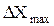> 20% (1996 и 1997 г.г.). Следовательно, месячное число н/с может приниматься в качестве базисного. Но таких месячных выборок три (1994, 1995 и 1998 г.г.), а ежемесячное число н/с неодинаково: 37,2; 37,6 и 34,3. Очевидно, что для повышения надежности анализа должно быть принято среднее из трех число н/с, т.е. 36.

Допустимость и надежность использования месячной выборки, во-первых, вполне доказывает тот факт, что рассчитанные коэф. вариации за различные по продолжительности периоды времени (от двух до пяти лет) во всех случаях были менее 15% и средний он составил 13,1%. Во-вторых, это позволяет сравнить травматизм завершившегося месяца с аналогичным месяцем предыдущего года, с предыдущим месяцем этого года и т.п. Результаты сопоставления, выполненного для каждого из месяцев всех пяти лет в целом по всем шахтам производственного объединения (360 шахтомесяцев), позволяют утверждать, что прогнозирование числа несчастных случаев на следующий месяц, а тем более квартал, полугодие, не сопровождается ошибками, превышающими ± 15%. Следовательно, такой прогноз может быть отнесен к достаточно надежным. Но одновременно необходимо отметить и подчеркнуть, что прогноз не может относиться к взрывам метановоздушной смеси по двум причинам:

- их нет в перечне аварий за пять лет; - прогноз взрывов метановоздушной смеси в шахтах – это вопрос особый, решение которого возможно только при выполнении специального, очень непростого исследования.

Однако вполне удовлетворительное применение методики для анализа травматизма на шахтах ПО «Снежноеантрацит» может быть следствием совпадения базисного числа н/с с месячным. Очевидно поэтому, что методику выбора числа несчастных случаев, необходимого для достоверного анализа, следует совершенствовать. Необходимость уточнения в первую очередь обусловливается тем, что как бы помесячная оценка базисного числа н/с является по существу дискретной и потому может привести к значительному её завышению. Покажем это, в частности, на конкретном примере приведенного обоснования принятия в качестве базисной месячного числа н/с. Предположим (что в общем случае совсем не исключено) приемлемым окажется число н/с не в месячной, а двухмесячной выборке, т.е. уже 72, что почти в 2 раза больше.

Такой резкий неоправданный рост н/с в базисной выборке недопустим, поэтому расчет должен уточняться следующим образом.

На рис. 4.А2 представлены построенные по данным о травматизме на шахтах ПО «Снежноеантрацит» зависимости 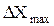, V, числа несчастных случаев N от исходной временной выборки (месячной – I, двухмесячной – II …). Теперь методика уточненного использования выбора числа н/с сводится к следующему поэтапному расчету.

На первом этапе, как и прежде, рассчитываются 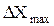и V для месячных, двух- и трехмесячных периодов времени, анализируется возможность выбора в качестве базисного месячного числа н/с. Если она подтверждается, расчет на этом заканчивается, а если нет, переходят к выполнению исследования второго этапа.

Строятся зависимости аналогичные 1 и 3 (рис. 4.А2.) и по ним при условии, что 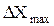< 20% не менее чем в трех случаях из пяти, а V £ 15% для любых нескольких лет выбирается число н/с в интервале между одним и двумя месяцами. Не исключаем возможность и того, что это будут II и III месяцы.