Задачи динамического программирования (ЗДП)

Общая задача динамического программирования формулируется следующим образом: пусть данная система S находится в начальном состоянии σ0 и является управляемой, после осуществления управляющего воздействия xi система переходит в другое состояние σi. Качество любого воздействия x_i характеризуется значением функции ƒ. Задача состоит в том, чтобы найти такие управляющие воздействия, которые оптимизируют функцию ƒ. При геометрической интерпретации допустимые состояния системы определяются точками n – мерного пространства. Каждому управляющему воздействию x_i соответствует траектория движения этой точки и из всех допустимых траекторий нужно найти такую, которая обеспечивает экстремальное значение функции.

Пример. Для осуществления своей деятельности предприятия должны периодически производить замену используемого оборудования учитывая его производительность (объем выпуска в единицу времени), затраты связанные с содержанием и ремонтом, стоимость приобретенного и заменяемого оборудования. Если к началу планируемого периода на предприятии установлено новое оборудование, позволяющее за t-й год выпустить готовую продукцию на сумму R(t) рублей, затраты на содержание составляют Z(t) рублей. Оборудование может быть продано за P(t) руб. и новое оборудование может быть куплено за S(t) руб. Необходимо найти такой план замены оборудования, который обеспечит максимальную прибыль.

Динамическое программирование – это процесс, в котором поэтапно планируют некоторый многошаговый процесс, при этом на каждом этапе оптимизируют только один шаг. Управление должно выбираться с учетом всех последствий в будущем. Для разработки методов решения задач динамического программирования существенно чтобы выполнялись следующие условия:

1. Целевая функция аддитивна, т.е. оптимизируемый критерий накоплен как сумма частных значений критерия на отдельных шагах:

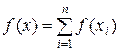или хотя бы возможно представление в виде произведения ƒ(х)=ƒ(х₁)* ƒ(х₂)*…* ƒ(х_n), тогда lnƒ(x)=∑ lnƒ(x_i); g(x)=∑g(x_i)

2. Новое состояние σ_i зависит только от предыдущего состояния σ_i-1 и оказываемого на систему воздействия x_i - управления, и не зависит от того, каким образом система пришла в состояние σ_i-1, т.е. выполняется условие отсутствия последствия.

Оптимальной стратегией управления называется вектор Х^*, координатами которого являются управления на каждом шаге, в результате реализации которых система за n шагов из начального состояния σ₀ переходит в конечное состояние σ_n, причем ƒ(x^*)=max_σ,x ƒ(x)

Теорема (принцип оптимальности) Каково бы не было состояние системы перед очередным шагом необходимо выбрать управление так, чтобы сумма значения оптимизируемого критерия на этом шаге и оптимального значения критерия на всех последующих шагах была максимальной, т.е. должно выполнятся основное функциональное уравнение Беллмана:

(**)

,

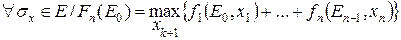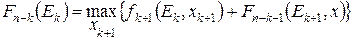где F_n(E₀) – это максимальное значение критерия оптимизации, получаемое за n шагов при переходе системы из E₀ в E_n при реализации оптимальной стратегии управления Х^*,

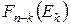- это максимальное значение, полученное при переходе из любого состояния E_k в конечное состояние E_n при оптимальной стратегии управления на оставшихся n-k шагах.

Полагая в уравнении (**) k=n-1 и считая известным F₀(E_n) (делаем некоторое предположение), получаем F₁(E_n-1)=max{ƒ_n(E_n-1,x_n)+F₀(E_n)}.

Рассматривая всевозможные допустимые состояния на n-1 шаге 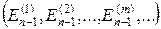, находим условно-оптимальное решение для каждого из этих состояний: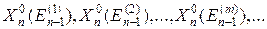 и находим соответствующие значения функции 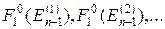т.е. на n-ом шаге будет найдено условно-оптимальное управление при любом допустимом состоянии системы после n-1 шага. Затем, полагая k=n-2, из (**) находим F₂(E_n-2)=max{ƒ_n-1(E_n-2,x_n-1)+F₁(E_n-1)}. При некотором наборе допустимых состояний E_n-2 и соответствующих управлений x_n-1, находим условно-оптимальное управление 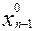для каждого из состояний 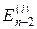. Последовательно осуществляя описанный итерационный процесс, дойдем до k=1 и выберем управление, которое является наилучшим с учетом условно- оптимальных управлений, принятых на всех предыдущих шагах. Т.о., пройдя все этапы от конца процесса к его началу, определим максимальное значение целевой функции за все n шагов и для каждого найдем условно-оптимальное управление. Затем проходим всю последовательность шагов от начала до конца процесса. На первом шаге полагаем: 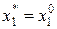, на втором шаге находим состояние 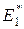из 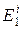в которое система перейдет под воздействием управления 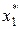. Это состояние определит найденное условно-оптимальное управление 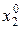, которое теперь считается оптимальным, т.е. 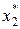найдено, и т.д. на n-ом шаге находим 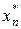, т.е 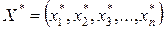и оптимальное значение критерия ƒ(x^*).

Итак, в динамическом программировании процесс рассматривается от конца к началу при различных предположениях о результатах окончания предпоследнего шага, и для каждого предположения выбирают управление на последнем шаге, которое запоминают до конца решения. Этот процесс повторяют на каждом шаге. Такое оптимальное управление называется условно-оптимальным. Изменив направление анализа, условно-оптимальное управление переводим в оптимальное.

Алгоритм решения задачи динамического программирования

1. На выбранном шаге задаем набор значений переменной управления, определяемый ограничениями задачи. Этот набор характеризует последний шаг, возможное состояние системы на предпоследнем шаге. Для каждого возможного состояния и каждого значения выбранной переменной вычисляем значение целевой функции. Из них для каждого исхода предпоследнего шага выбираем оптимальные значения целевой функции и соответствующие им значения рассматриваемой переменной управления. Запоминаем оптимальное значение переменной управления и соответствующие значение целевой функции. Составляем таблицу значений.

2. Переходим к оптимизации на следующем шаге при любом значении новой переменной управления и при оптимальных значениях переменных управления, полученных ранее. Оптимальное значение целевой функции на последующих шагах считывают из предыдущей таблицы. Если новая переменная характеризует 1-й шаг, то переходим к п.3, в противном случае, повторяем п.2 для следующей переменной.

3. При заданном исходном условии для каждого возможного значения первой переменной управления вычисляем значение целевой функции и выбираем оптимальное значение целевой функции вместе с соответствующим оптимальным значением управления.

4. При известном оптимальном значении первой переменной управления определяем исходные данные для следующего шага и из последней таблицы определяем оптимальные значения следующей переменной.

5. Если следующая переменная не характеризует последний шаг, то переходим к пункту 4, иначе, к пункту 6.

6. Выписываем оптимальное решение из всех полученных таблиц.

Пример. Задача об оптимальной загрузке транспортного средства неделимыми предметами.

Требуется погрузить в самолет 4 вида предметов, масса каждого из которых P_i соответственно равна 24; 22; 16; 10. Соответствующая эффективность V_i каждого предмета равна 96; 85; 50; 20 ед. Известна общая грузоподъемность самолета W=83. Нужно найти такой план погрузки X, который максимизирует эффект перевозок. X_i – число предметов i-го вида взятых на борт самолета.

Решение:

Итерационный процесс состоит из 4 шагов. Каждый шаг рассматривает вариант загрузки предметами с добавлением только одного вида предметов.

1-й шаг. Заполняем самолет предметами 1-го вида. При этом эффективность составит ƒ₁(х₁)=96*х₁

X1	ƒ(x1)	W
		[0,23]
		[24,47]
		[48,71]
		[72,83]

Рассмотрим загрузку предметов 1-го вида и 2-го вида. Максимальная эффективность равна: ƒ₂(x₂)=max{x₂V₂+ƒ₁(W-x₂P₂)} ƒ₁(W-x₂P₂)=max{(W-x₂P₂)*V₁}

W	X2	X2V2	W-X2P2	ƒ1(W-X2P2)	ƒ2	ƒ2(W)
[0;21]
[22;23]
[24;43]	0,1	0,85	24,2	96,0	96,85
[44;45]	0,1,2	0,85,170	44,22,0	96,0,0	96,85,170
[46;47]	0,1,2	0,85,170	46,24,2	96,96,0	96,181,170
[48;65]	0,1,2	0,85,170	48,26,4	192,96,0	192,181,170
[66;67]	0,1,2,3	0,85,170,255	66,44,22,0	192,96,0,0	192,181,170,255
[68;69]	0,1,2,3	0,85,170,255	68,46,24,2	192,96,96,0	192,181,266,255
[70;71]	0,1,2,3	0,85,170,255	70,48,26,4	192,192,96,0	192,277,266,255
[72;83]	0,1,2,3	0,85,170,255	72,50,28,6	288,192,96,0	288,277,266,255

ƒ₃(x₃)=max{x₃V₃+ƒ₂(W-x₃P₃)}

W	X3	X3V3	W-X3P3	ƒ2(W-X3P3)	ƒ3	ƒ3(W)
[0;15]
[16;21]
[22;23]	0,1	0,50	22,6	85,0	85,50
[24;31]	0,1	0,50	24,8	96,0	96,50
[32;37]	0,1,2	0,50,100	32,16,0	96,0,0	96,50,100
[38;43]	0,1,2	0,50,100	38,22,6	96,85,0	96,135,100
[44;45]	0,1,2	0,50,100	44,28,12	170,96,0	170,146,100
[46;47]	0,1,2	0,50,100	46,30,14	181,96,0	181,146,100
[48;63]	0,1,2,3	0,50,100,150	48,32,16,0	192,96,0,0	192,146,100,150
[64;69]	0,1,2,3,4	0,50,100,150,200	64,48,32,16,0	192,192,96,0,0	192,242,196,150,200
[70;71]	0,1,2,3,4	0,50,100,150,200	70,54,38,22,6	277,192,96,0,0	277,242,196,150,200
[72;83]	0,1,2,3,4,5	0,50,100,150,200,250	72,56,40,24,8	288,192,96,96,0,0	288,242,196246,200,250

Заполнение подробной таблицы для 4-го продукта не требуется, т.к. нет продукта 5-го вида.

В результате шагов 1-4 получено условно оптимальное решение. На 2-ом этапе будем строить оптимальное решение. Из таблицы 4-го шага было получено, что х₄^*=1 и при этом ƒ₄=308. Тогда заключаем, что нужно брать 1 единицу груза 4-го вида, тогда остаточная грузоподъемность W_ост=83-10=73. Из таблицы №3 находим диапазон, в котором находится W_ост → х₃^*=0 (0 единиц груза вида 3). Из таблицы №2 находим диапазон с W_ост → х₂^*=0 (0 единиц груза 2 вида). Из таблицы №1 находим, что х₁^*=3 (3 единицы груза вида 1).

Пример. Для увеличения объемов выпуска пользующейся повышенным спросом продукции, изготовляемой предприятиями, выделены капиталовложения в объеме S = 700 тыс. рублей. Использование i-ым предприятием Х_i тыс.рублей из указанных средств обеспечивает прирост выпуска продукции, определяемый значениями нелинейной функции f_i(X_i). Значения Х_i и f_i (X_i) приведены в таблице.

Объем капиталовложений Xi (тыс. руб.)	Прирост выпуска продукции fi (Xi) в зависимости от объема капиталовложений (тыс. руб.)
Предприятие 1	Предприятие 2	Предприятие 3

Решение. Для решения данной задачи динамического программирования составляется рекуррентное соотношение Беллмана и, используя данные исходной таблицы, определяются сначала условно оптимальные, а затем и оптимальные распределения капиталовложений между предприятиями.

Начинается решение с определения условно оптимальных капиталовложений, выделяемых для развития первого предприятия. Для этого находятся значения φ₁ (Х) для каждого Х, принимающего значения 0, 100, 200, 300, 400, 500, 600 и 700.

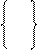Пусть Х = 0, тогда φ₁ (0) = 0.

Х = 100, тогда φ₁ (100) = max = 30, X⁰₁ = 100.

Здесь первая строка соответствует решению Х₁ = 0, а вторая строка – решению Х₁ = 100. Так как при первом решении прирост выпуска продукции не обеспечивается, а при втором равен 30 тыс. рублей, то условно оптимальным решением является X⁰₁ = 100. Аналогично находятся условно оптимальное решение для других значений Х:

φ₁ (200) = max = 50, X⁰₁ = 200; φ₁ (300) = max = 90, X⁰₁ = 300;

φ₁ (400) = max = 110, X⁰₁ = 400; φ₁ (500) = max = 170, X⁰₁ =500;

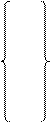
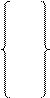
φ₁ (600) = max = 180, X⁰₁ = 600; φ₁ (700) = max = 210, X⁰₁ = 700.

Результаты вычислений и полученные соответствующие условно-оптимальные решения записываются в таблицу:

Объем капиталовложений X, выделяемых первому предприятию (тыс. руб.)	Максимальный прирост φ1 (Х) выпуска продукции (тыс. руб.)	Условно оптимальный объем капиталовложений Х01, выделяемых первому предприятию (тыс. руб.)

Используя исходные данные и последней таблицы, определяем условно-оптимальные объемы капиталовложений, выделяемых второму предприятию. Находятся 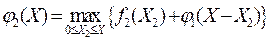для каждого из допустимых значений Х, равных 0, 100, 200, 300, 400, 500, 600 и 70:

0+50 50+30 80+0

φ₂ (0) = 0, X⁰₂ = 0;

φ₂(100) = max = 50, X⁰₂ = 100; φ₂(200) = max = 80, X⁰₂ = 100;

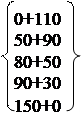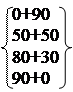φ₂(300)=max = 110, X⁰₂ = 200; φ₂(400)=max = =1=150, X⁰₂ =400;

φ₂(500) = max =190, X⁰₂ =500; φ₂(600)=max = 220,X⁰₂=100;

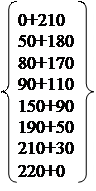φ₂(700) = max = 250, X⁰₂ = 200;

Полученные результаты и найденные условно-оптимальные объемы капиталовложений, выделяемых второму предприятию, записываются в таблицу.

Объем капиталовложений X, выделяемых двум предприятиям (тыс. руб.)	Максимальный прирост φ2(Х) выпуска продукции (тыс. руб.)	Условно оптимальный объем капиталовложений Х02, выделяемых второму предприятию (тыс. руб.)

Для нахождения значений φ₃(Х) используются данные предыдущей и исходной таблиц. Переходим к нахождению значений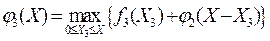

Так как в данном случае число предприятий равно 3, то подробная таблица для всех Х не нужна, и проводится вычисление лишь для одного значения Х = 700:

φ₃(700) = max = 270, X⁰₃ = 600.

Следовательно, максимальный прирост выпуска продукции составляет 270 тыс. рублей. Это имеет место тогда, когда третьему предприятию выделяется 600 тыс. рублей, а первому и второму предприятиям – 100 тыс. рублей. Тогда, как видно из таблицы, второму предприятию следует выделить 100 тыс. рублей. Таким образом, получается оптимальный план распределения капиталовложений между предприятиями, согласно которому обеспечивается максимальный прирост выпуска продукции [1, C. 305-310].