Приближенные методы решения ЗНЛП

Используя градиентные методы, можно найти решение любой ЗНЛП.

Метод Франка-Вульфа применим, если ƒ(x1, x2, …, xn)→max и является вогнутой функцией на выпуклом множестве Ω, т.е.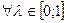

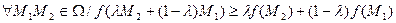
При условиях ∑aijxj≤bi; i=1;m; xj≥0, то применяется следующий алгоритм:

Найти исходное допустимое решение задачи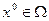

Найти градиент функции ƒ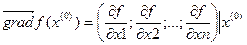

Построить функцию

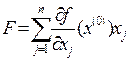; найти ее максимальное значение Z(k)

По формул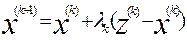е , где 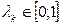- произвольно, или находится как наименьшее решение уравнения 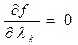, найти новое приближение х(k).

Проверить необходимость перехода к последующему допустимому решению, приняв в качестве критерия оценки неравенство

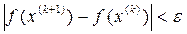. Если неравенство не выполнено, тогда переходим к пункту 2, где x(0)=х (к), в противном случае решение задачи найдено.

Метод штрафных функций применим, если ƒ(x1, x2, …, xn)→max

и ƒ вогнутая на Ω Ω: g_i(x1, x2,…, xn)≤b_i x_j≥0, где g_i - выпуклые функции.

Алгоритм метода:

1. Найти исходное допустимое решение задачи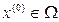

2. Выбрать шаг вычислений

3. Найт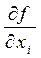и и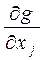

4. По формуле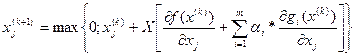

Определить координаты точки определяющей новое решение задачи, где α_i(x₁,x₂,…,x_n)=0, если b_i-g_i(x₁,…x_n)≥0 и α_i(x₁,x₂,…,x_n)=α_i,

если b_i-g_i<0 и α_i – весовые коэффициенты.

Начинают итерационный процесс при малых α_i, постепенно их увеличивая.

5. Проверяют, удовлетворяют ли координаты найденной точки системе ограничений задачи. Если нет, то переходят к следующему этапу, если да, то определяют необходимость перехода к следующему допустимому решению по формуле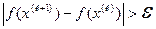

В случае необходимости переходят к этапу 2, в противоположном случае решение найдено.

6. Устанавливают значение весовых коэффициентов и переходят к этапу 4

Замечание: произвольный выбор значений α_i приводит к значительным колебаниям удаленности определяемых точек от области допустимых решений. Этот недостаток устраняется при решении задачи методом Эрроу – Гурвица, согласно которому на очередном шаге числа α_i выбирают по формуле: 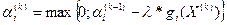, где α_i ⁽⁰⁾ – произвольное положительное число.

Пример. Найти методом штрафных функций максимальное значение функции f = -x²₁ – x²₂

при условиях

(x₁–7)² + (x₂ – 7)² ≤ 18, (14)

x₁;x₂≥ 0. (15)

Решение. Целевая функция данной задачи представляет собой отрицательно-определенную квадратичную форму и, значит, вогнута. В то же время область допустимых решений задачи, определяемая ограничениями (14) и (15), - выпуклая. Следовательно, данная задача является задачей выпуклого программирования. Для нахождения ее решения применяется метод штрафных функций.

Полагается Х⁽⁰⁾ = (6, 7). Берется λ = 0,1. Обозначается через

g (x₁, x₂) = 18 - (x₁ – 7)² - (x₂ – 7)² и определяются частные производные от функций f (x₁, x₂) и g (x₁, x₂) по переменным х₁ и х₂:

∂f/∂х₁ = -2x₁;

∂g/∂х₁ = -2x₁ +14;

∂f/∂х₂ = -2x₂;

∂g/∂х₂ = -2x₂ + 14.

Теперь, используя формулу (12), строятся последовательности точек, одна из которых определит приемлемое решение.

I итерация. Так как точка Х⁽⁰⁾ = (6, 7) принадлежит области допустимых решений задачи, то второе слагаемое в квадратных скобках формулы (12) равно нулю. Значит координаты следующей точки Х⁽¹⁾ вычисляются по формулам

х₁⁽¹⁾ = max {0; x₁⁽⁰⁾ + λ (∂f (X⁰)/∂х₁)} = max {0; 6 + 0,1 * (-2) * 6} = 4,8;

х₂⁽¹⁾ = max {0; x₂⁽⁰⁾ + λ (∂f (X⁰)/∂х₂)} = max {0; 7 + 0,1 * (-2) * 7} = 5,6.

Проверяется теперь, принадлежит ли эта точка области допустимых решений задачи. Для этого находится g (X⁽¹⁾) = 18 – 4,48 – 1,96 = 11,2. Так как g (X⁽¹⁾) > 0, тоX⁽¹⁾ принадлежит области допустимых решений. В этой точке f (X⁽¹⁾) = -54,4.

II итерация. Находятся

х₁⁽²⁾ = max {0; 0,48 + 0,1 * (-2) * 4,8} = 3,84;

х₂⁽²⁾ = max {0; 0,56 + 0,1 * (-2) * 5,6} =4,48;

g (X⁽²⁾) = 18 – 9,9856 – 6,3504 = 1,664 > 0;

f (X⁽²⁾) = -34,816.

III итерация. Находятся

х₁⁽³⁾ = max {0; 0,384 + 0,1 * (-2) * 3,84} = 3,072;

х₂⁽³⁾ = max {0; 0,448 + 0,1 * (-2) * 4,48} =3,584;

g (X⁽³⁾) = 18 –15,429184 – 11,669056 ≈ -9,0981.

IV итерация. Точка Х⁽³⁾ не принадлежит области допустимых решений задачи. Следовательно,

х₁⁽⁴⁾ = max {0; x₁⁽³⁾ + λ [(∂f (X³)/∂х₁) + α (∂g (X⁽³⁾)/ ∂x₁)]} = max {0; 3,072 + 0,1 * [(-2) * 3,072 + α [(-2) * 3,072 + 14)]} = max {0; 2,4576 + α * 0,7856};

х₂⁽⁴⁾ = max {0; x₂⁽³⁾ + λ [(∂f (X³)/∂х₂) + α (∂g (X⁽³⁾)/ ∂x₂)]} = max {0; 3,584 + 0,1 [(-2) * 3,584 + α ((-2) * 3,584)]} = max {0; 2,8672 + α * 0,6832}.

Чтобы выбрать число α, целесообразно взять его так, чтобы точка Х⁽⁴⁾ не слишком далеко удалялась то границы области допустимых решений и вместе с тем принадлежала этой области. Этим требованиям удовлетворяет, в частности, α = 1,9. При данном значении получается

х₁⁽⁴⁾ = max {0; 2,4576 + 1,9 * 0,7856} ≈ 3,95;

х₂⁽⁴⁾ = max {0; 2,8672 + 1,9 * 0,6832} ≈ 4,165;

g (X⁽⁴⁾) = 18 – 9,3025 – 8,037225 ≈ 0,66;

f (X⁽⁴⁾) ≈ -32,95.

V итерация. Находятся

х₁⁽⁵⁾ = max {0; 3,95 + 0,1 * (-2) * 3,95} ≈ 3,16;

х₂⁽⁵⁾ = max {0; 4,165 + 0,1 * (-2) * 4,165 } ≈ 3,332;

g (X⁽⁵⁾) = 18 – 14,7456 – 13,454224 ≈ -10,2.

VI итерация. Находятся

х₁⁽⁶⁾ = max {0; 3,16 + 0,1 * [(-2) * 3,16 + 1,9 * ((-2) * 3,16 + 14)]} ≈ 3,987;

х₂⁽⁶⁾ = max {0; 3,332 + 0,1 * [(-2) * 3,332 + 1,9 * ((-2) * 3,332 + 14)]} ≈ 4,059;

g (X⁽⁶⁾) = 18 – 9,078169 – 8,649481 ≈ 0,272;

f (X⁽⁶⁾) ≈ -32,372.

VII итерация. Находятся

x₁⁽⁷⁾ = max {0; 3,987 + 0,1 * (-2) * 3,987} ≈ 3,189;

x₂⁽⁷⁾ = max {0; 4,059 + 0,1 * (-2) * 4,059 } ≈ 3,247;

g (X⁽⁷⁾) = 18 – 10,169721 – 10,543009 ≈ -2,713.

VIII итерация. Находятся

х₁⁽⁸⁾ = max {0; 3,189 + 0,1 * [(-2) * 3,189 + 1,9 * ((-2) * 3,189 + 14)]} ≈ 3,999;

х₂⁽⁸⁾ = max {0; 3,247 + 0,1 * [(-2) * 3,247 + 1,9 * ((-2) * 3,247 + 14)]} ≈ 4,024;

g (X⁽⁸⁾) = 18 – 9,006001 – 8,856576 ≈ 0,137;

f (X⁽⁸⁾) ≈ -32,185.

IX итерация. Находятся

x₁⁽⁹⁾ = max {0; 3,999 + 0,1 * (-2) * 3,999} ≈ 3,199;

x₂⁽⁹⁾ = max {0; 4,024 + 0,1 * (-2) * 4,024} ≈ 3,219;

g (X⁽⁹⁾) = 18 – 14,447601 – 14,295961 ≈ -10,744.

X итерация. Находятся

х₁⁽¹⁰⁾ = max {0; 3,199 + 0,1 * [(-2) * 3,199 + 1,9 * ((-2) * 3,199 + 14)]} ≈ 4,004;

х₂⁽¹⁰⁾ = max {0; 3,219 + 0,1 * [(-2) * 3,219 + 1,9 * ((-2) * 3,219 + 14)]} ≈ 4,012;

g (X⁽¹⁰⁾) = 18 – 8,976016 – 8,928144 ≈ 0,096;

f (X⁽¹⁰⁾) ≈ -32,128.

XI итерация. Находятся

x₁⁽¹¹⁾ = max {0; 4,004 + 0,1 * (-2) * 4,004} ≈ 3,203;

x₂⁽¹¹⁾ = max {0; 4,012 + 0,1 * (-2) * 4,012} ≈ 3,21;

g (X⁽¹¹⁾) = 18 – 14,417209 – 14,3641 ≈ -10,781.

XII итерация. Находятся

х₁⁽¹²⁾ = max {0; 3,203 + 0,1 * [(-2) * 3,203 + 1,9 * ((-2) * 3,203 + 14)]} ≈ 4,005;

х₂⁽¹²⁾ = max {0; 3,21 + 0,1 * [(-2) * 3,21 + 1,9 * ((-2) * 3,21 + 14)]} ≈ 4,008;

f (X⁽¹²⁾) ≈ -32,104.

Сравнивая значения целевой функции, найденные в точках, полученных после X и XII итераций, видно, что они с точностью до 10^-1 совпадают. Это означает близость точки, найденной на последней итерации, к точке максимального значения целевой функции. Так как точка Х⁽¹²⁾ находится вблизи границы области допустимых решений (поскольку g(X⁽¹²⁾)≈0,078), то х^*₁=4,005 и х^*₂=4,012 можно считать приемлемым решением задачи. Это решение при необходимости можно уточнить дальнейшими шагами.

Пример. Используя метод Эрроу-Гурвица, найти решение предыдущей задачи.

Решение. Как следует из решения предыдущей задачи, при нахождении решения этой задачи методом Эрроу-Гурвица первые три итерации при одинаковых значениях λ = 0,1 в обоих случаях совпадают. Это объясняется тем, что каждая из последовательно получаемых точек принадлежит области допустимых решений, а поэтому α_i^(k) = 0 (k = 1, 2, 3) независимо от того, находится ли оно по формуле (1) или (3).

IV итерация. Так как g (X⁽³⁾) < 0, то координаты следующей точки находятся по формуле (2):

х₁⁽⁴⁾ = max {0; x₁⁽³⁾ + λ * [(∂f (X⁽³⁾)/∂х₁) + α⁽⁴⁾ * (∂g (X⁽³⁾) /∂х₁)]} =

=max {0; 3,072 + 0,1 * [(-2) * 3,072 + α⁽⁴⁾ * ((-2) * 3,072 + 14)]};

х₂⁽⁴⁾ = max {0; x₂⁽³⁾ + λ * [(∂f (X⁽³⁾)/∂х₂) + α⁽⁴⁾ * (∂g (X⁽³⁾) /∂х₂)]} =

= max {0; 3,584 + 0,1 * [(-2) * 3,584 + α⁽⁴⁾ * ((-2) * 3,072 + 14)]}.

Число α⁽⁴⁾ находится по формуле (2.21):

α⁽⁴⁾ = max {0; α⁽³⁾ - 0,1 * g(X⁽³⁾)} = max {0; 0 – 0,1 * (-9,0981)} ≈ 0,91.

Таким образом, х₁⁽⁴⁾ ≈ 3,172; х₂⁽⁴⁾ ≈ 3,489; g (X⁽⁴⁾) ≈ -8,981.

V итерация. Найденная точка Х⁽⁴⁾ = (3,172; 3,489) не принадлежит области допустимых решений исходной задачи. Поэтому отыскиваются координаты следующей точки, предварительно найдя α.

α⁽⁵⁾ = max {0; 0,91 – 0,1 * (-8,981)} ≈ 1,81.

х₁⁽⁵⁾ = max {0; 3,172 + 0,1 * [(-2) * 3,172 + 1,81 * ((-2) * 3,172 + 14)]} ≈ 3,923;

х₂⁽⁵⁾ = max {0; 3,489 + 0,1 * [(-2) * 3, 489 + 1,81 * ((-2) * 3, 489 + 14)]} ≈ 4,062;

g (X⁽⁵⁾) ≈ -0,1.

VI итерация. Находятся

α⁽⁶⁾ = max {0; 1,81 – 0,1 * (-0,1)} ≈ 1,82;

х₁⁽⁶⁾ = max {0; 3,923 + 0,1 * [(-2) * 3, 923 + 1,82 * ((-2) * 3, 923 + 14)]} ≈ 4,258;

х₂⁽⁶⁾ = max {0; 4,062 + 0,1 * [(-2) * 4,062 + 1,82 * ((-2) * 4,062 + 14)]} ≈ 4,319;

g (X⁽⁶⁾) ≈ 1,294;

f (X⁽⁶⁾) ≈ -36,784.

VII итерация. Находятся

х₁⁽⁷⁾ = max {0; 4,258 + 0,1 * [(-2) * 4,258]} ≈ 3,406;

х₂⁽⁷⁾ = max {0; 4,319 + 0,1 * [(-2) * 4,319]} ≈ 3,455;

g (X⁽⁷⁾) ≈ -7,484.

VIII итерация. Находятся

α⁽⁸⁾ = max {0; 1,82 – 0,1 * (-7,484)} ≈ 2,57;

х₁⁽⁸⁾ = max {0; 3,406 + 0,1 * [(-2) * 3,406 + 2,57 * ((-2) * 3,406 + 14)]} ≈ 4,572;

х₂⁽⁸⁾ = max {0; 3,455 + 0,1 * [(-2) * 3,455 + 2,57 * ((-2) * 3,455 + 14)]} ≈ 4,586;

g (X⁽⁸⁾) ≈ 6,278;

f (X⁽⁸⁾) ≈ -41,935.

IX итерация. Находятся

х₁⁽⁹⁾ = max {0; 4,572 + 0,1 * [(-2) * 4,572]} ≈ 3,658;

х₂⁽⁹⁾ = max {0; 4,586 + 0,1 * [(-2) * 4,586]} ≈ 3,669;

g (X⁽⁹⁾) ≈ -4,265.

X итерация. Находятся

α⁽¹⁰⁾ = max {0; 2,57 – 0,1 * (-4,265)} ≈ 3;

х₁⁽¹⁰⁾ = max {0; 3,658 + 0,1 * [(-2) * 3,658 + 3 * ((-2) * 3,658 + 14)]} ≈ 4,931;

х₂⁽¹⁰⁾ = max {0; 3,669 + 0,1 * [(-2) * 3,669 + 3 * ((-2) * 3,669 + 14)]} ≈ 4,934;

g (X⁽¹⁰⁾) ≈ 9,451.

XI итерация. Находятся

х₁⁽¹¹⁾ = max {0; 4,931 + 0,1 * [(-2) * 4,931]} ≈ 3,945;

х₂⁽¹¹⁾ = max {0; 4,934 + 0,1 * [(-2) * 4,934]} ≈ 3,947;

g (X⁽¹¹⁾) ≈ -0,654.

XII итерация. Находятся

α⁽¹²⁾ = max {0; 3 – 0,1 * (-0,654)} ≈ 3,06;

х₁⁽¹²⁾ = max {0; 3,945 + 0,1 * [(-2) * 3,945 + 3,06 * ((-2) * 3,945 + 14)]} ≈ 5,026;

х₂⁽¹²⁾ = max {0; 3,947 + 0,1 * [(-2) * 3,947 + 3,06 * ((-2) * 3,947 + 14)]} ≈ 5,026;

g (X⁽¹²⁾) ≈ 10,207; f (X⁽¹²⁾) ≈ -50,521.

XIII итерация. Находятся

х₁⁽¹³⁾ = max {0; 5,026 + 0,1 * [(-2) * 5,026]} ≈ 4,021;

х₂⁽¹³⁾ = max {0; 5,026 + 0,1 * [(-2) * 5,026]} ≈ 4,021;

g (X⁽¹³⁾) ≈ 0,251; f (X⁽¹³⁾) ≈ -32,337.

Полученное на данной итерации решение х^*₁ = 4,021 и х^*₂ = 4,021 можно считать приемлемым. Это решение при необходимости следует улучшить, продолжив итерационный процесс до получения результата требуемой точности.