Первый эффективный алгоритм решения задачи нахождения кратчайшего пути в графе между двумя вершинами, при условии, что все дуги графа имеют положительную длину, предложил в 1959 г. Е.Дейкстра.
Алгоритм 3.Алгоритм Дейкстры.
Начальная установка. Все вершины и дуги графа не окрашены. Каждой вершине в ходе выполнения алгоритма приписывается число (пометка) d (x), равное длине пути из начальной вершины S в вершину x. Причем, если вершина x окрашена, то d (x) - длина кратчайшего пути из S в x (постоянная пометка).
Положить d (x)=¥ для всех вершин x.
Шаг 1. Положить d (S)=0, y = S и окрасить вершину S. Здесь y - последняя из окрашенных вершин.
Шаг 2. Для каждой неокрашенной вершины x следующим образом пересчитать величину d (x):
d (x)=min{ d (x), d (y)+ a (y, x)}, (6.1)
где a (y, x) -длина дуги (y, x). Если d (x)= ¥ для всех неокрашенных вершин x, закончить процедуру: в исходном графе отсутствует путь из вершины S в неокрашенные вершины. В противном случае окрасить ту из вершин x, для которой величина d (x) является наименьшей. Кроме того, окрасить дугу, ведущую в выбранную на данном шаге вершину x (для этой дуги достигается минимум в соответствии с выражением 6.1). Положить y = x.
|
|
|
Шаг 3. Если y = t, закончить процедуру: кратчайший путь из S в t, состоящий из окрашенных дуг, найден. Его длина равна d (t). В противном случае перейти к шагу 2.
Отметим, что каждый раз, когда окрашивается некоторая вершина (не считая вершину S), окрашивается и некоторая дуга, заходящая в данную вершину. Таким образом, на любом этапе алгоритма в каждую вершину заходит не более чем одна окрашенная дуга. Кроме того, окрашенные дуги не могут образовывать в исходном графе цикл, так как в алгоритме не может окрашиваться дуга, концевые вершины которой уже окрашены. Следовательно, окрашенные дуги образуют в исходном графе ориентированное дерево с корнем в вершине S. Такое дерево называют деревом кратчайших путей.
Рассмотрим работу алгоритма 3 при поиске кратчайшего пути из вершины S в вершину t в графе, изображенном на рисунке 3.19. Результаты работы алгоритма сведены в табл. 3.8. Дерево кратчайших путей представлено на рис. 3.20.
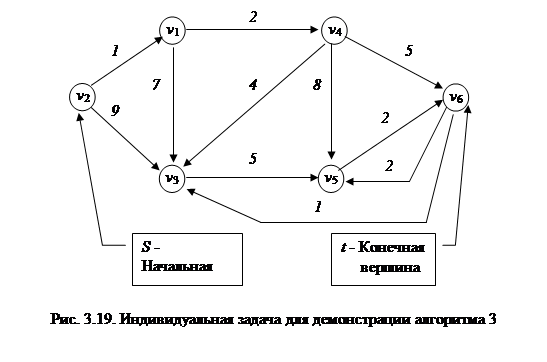 |
Таблица 3.8.
Этапы поиска кратчайшего пути из вершины S в вершину t в графе,
изображенном на рис. 3.19, согласно алгоритму 3
| Номер итерации (шаг) | Изменение величин d (x) для неокрашенных вершин | Окрашивание | |
| дуг | вершин | ||
| Нач.уст. | d (v i)=µ, i=1,…,6 | - | - |
| 1 (Шаг 1) | d (S)= d (v 2)=0 | - | y = v 2 |
| 2 (Шаг 2) | d (v 1)=min{ d (v 1), d (y)+ a (y, v 1)}= min{µ,0+1}=1 d (v 3)=min{ d (v 3), d (y)+ a (y, v 3)}= min{µ,0+9}=9 | (v 2, v 1) | y = v 1 y ¹ t |
| 3 (Шаг 2) | d (v 3)=min{9,1+7}=8 d (v 4)=min{µ,1+2}=3 | (v 1, v 4) | y = v 4 y ¹ t |
| 4 (Шаг 2) | d (v 3)=min{8,3+4}=7 d (v 5)=min{µ,3+8}=11 d (v 6)=min{µ,3+5}=8 | (v 4, v 3) | y = v 3 y ¹ t |
| 5 (Шаг 2) | d (v 5)=min{11,7+5}=11 d (v 6)=8 (Посчитано на 4 итерации) | (v 4, v 6) | y = v 6 y = t КОНЕЦ |
 |
|
|
|
Корректность алгоритма поясняется следующими рассуждениями. Обратим внимание на тот факт, что существенным образом используется положительность весов дуг. Пусть на некотором этапе А и В - множества вершин с постоянными и временными пометками. В конце шага 2 всякая временная пометка - это длина кратчайшего пути между вершиной S и помеченной вершиной, проходящего только через вершины множества А. Но при этом оказывается, что для вершины x, окрашиваемой на шаге 2 - это вообще длина кратчайшего пути из S в x. Действительно, если бы это было не так, то в В существовала бы вершина x ¢, через которую проходит кратчайший путь из S в x. При этом за x ¢ можно взять такую вершину на этом пути, что все предшествующие x ¢ вершины пути лежат в множестве А. Пусть a и b - длины частей этого пути от S к x ¢ и от x ¢ к x. Так как веса всех дуг положительны, то a, b >0. Так как этот путь кратчайший, то a+b< d (x), но отсюда следует, что a= d (x ¢)< d (x). А это соотношение противоречит минимальности пометки x среди всех временных пометок вершин.
На каждой итерации работы алгоритма ровно одна временная пометка становится постоянной, поэтому алгоритм завершает работу не более чем за n итераций. На каждой итерации просматривается n вершин. Таким образом, трудоемкость алгоритма Дейкстры О(n 2).
Выделим теперь свойство задачи, которое допускает её правильное решение описанным алгоритмом. Любая часть решения также является решением, то есть если S, x 1,..., xn, t - кратчайший путь из S в t, то для любого i =1,2,..., n путь S, x 1,..., xi является кратчайшим из S в xi. Подобное свойство является одним из важнейших свойств метода, известного под названием динамического программирования.
«Динамическое программирование, в сущности, вычисляет решение для всех подзадач. Вычисление идет от малых подзадач к большим, ответы запоминаются в таблице. Преимущество этого метода состоит в том, что раз уж эта задача решена, её ответ где-то хранится и никогда не вычисляется заново» [8]. В алгоритме Дейкстры на каждом шаге решается некоторая подзадача, а именно: находится кратчайший путь из начальной вершины S в некоторую вершину x. Результат её решения – длина кратчайшего пути из S в x (постоянная пометка вершины x) запоминается в массиве и далее не пересчитывается.
 2015-04-01
2015-04-01 1335
1335








