Также как и при генерации сочетания будем считать, что элементами множества являются целые числа от 1 до n.
Последовательность перестановок на множестве {1,2,..., n } представлена в лексикографическом порядке, если она записана в порядке возрастания получающихся чисел. Например, лексикографическая последовательность перестановок трех элементов имеет вид 123, 132, 213, 231, 312, 321.
Порождать такую последовательность можно следующим образом. Начиная с перестановки Р =(1,2,..., n), переходим к следующей, путем просмотра текущей справа налево с целью поиска самой правой позиции, в которой рi < рi +1. Найдя ее, ищем рj, наименьший элемент, расположенный справа от рi и больше его. Затем осуществляется транспозиция элементов рi и pj и отрезок рi +1,..., рn (элементы которого расположены в порядке убывания) переворачивается. Например, для n =8 имеем текущую перестановку p =(2,6,5,8,7,4,3,1), тогда рi =5 (i =3) и рj =7 (j =5). Меняя их местами и переворачивая p 4, p 5, p 6, p 7, p 8, получаем следующую перестановку (2,6,7,1,3,4,5,8). Эту процедуру реализует алгоритм представленный на рис.2.8.
Рассмотрим еще один алгоритм порождения перестановок. Этот алгоритм генерирует перестановки в порядке минимального изменения, т.е. перестановка отличается от предшествующей транспозицией двух соседних элементов.
Такую последовательность перестановок можно построить рекурсивно. Для n =1 существует единственная перестановка (1). Предположим, что построена последовательность перестановок П1,П2,...,П( n -1)! на множестве {1,2,..., n -1} в порядке минимального изменения.
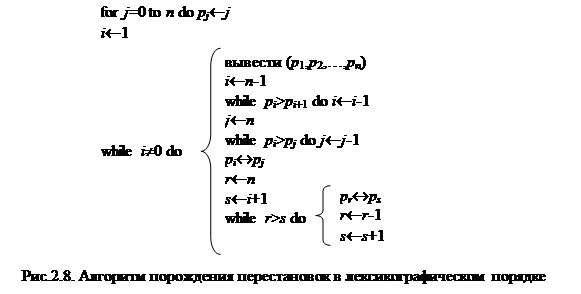 |
 Расширим каждую из (n -1)! этих перестановок путем вставки элемента n на каждое из n возможных мест. Причем, элемент n добавляется к П i последовательно во все позиции справа налево, если i нечетное, и слева направо, если i четное. Пример такого расширения представлен на рис.2.9.
Расширим каждую из (n -1)! этих перестановок путем вставки элемента n на каждое из n возможных мест. Причем, элемент n добавляется к П i последовательно во все позиции справа налево, если i нечетное, и слева направо, если i четное. Пример такого расширения представлен на рис.2.9.
Эту же последовательность перестановок можно порождать итеративно, получая каждую перестановку из предшествующей и добавочной информации. Это делается с помощью трех векторов: текущей перестановки Р =(р 1,..., рn), обратной к ней перестановки 0 =(о 1,..., оn) (о 1 - индекс наименьшего элемента в Р, о 2 - индекс следующего по величине элемента в Р и т.д., следовательно, 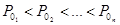 ) и записи направления D =(d 1,..., dn), в котором сдвигаются элементы перестановки (di =-1, если pi сдвигается влево, di =1 - вправо, di =0 - не сдвигается). Элемент сдвигается до тех пор, пока не достигнет элемента большего чем он сам; в этом случае сдвиг прекращается. В этот момент направление сдвига данного элемента изменяется на противоположное и передвигается следующий меньший его элемент, который можно сдвинуть. Поскольку хранится перестановка, обратная к Р, то в Р легко найти место следующего меньшего элемента. Эту процедуру реализует алгоритм представленный на рис.2.10.
) и записи направления D =(d 1,..., dn), в котором сдвигаются элементы перестановки (di =-1, если pi сдвигается влево, di =1 - вправо, di =0 - не сдвигается). Элемент сдвигается до тех пор, пока не достигнет элемента большего чем он сам; в этом случае сдвиг прекращается. В этот момент направление сдвига данного элемента изменяется на противоположное и передвигается следующий меньший его элемент, который можно сдвинуть. Поскольку хранится перестановка, обратная к Р, то в Р легко найти место следующего меньшего элемента. Эту процедуру реализует алгоритм представленный на рис.2.10.
Заметим, что в данном алгоритме Р 0 и Pn +1 инициализируются величиной n +1, чтобы прекратить передвижение n, и d 1 инициализируется нулем, чтобы в тех случаях, когда m становятся равным единице во внутреннем цикле, остаток внешнего цикла был правильно определен.
Алгоритм порождения случайных перестановок представлен на рис.2.11. Данный алгоритм аналогичен алгоритму порождения случайных сочетаний (рис.2.7).
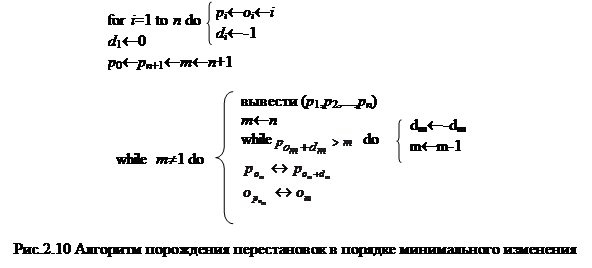 |
 |
 2015-04-01
2015-04-01 2516
2516








