Как было сказано выше между n -разрядными двоичными наборами (целыми числами от 0 до 2n-1) и подмножествами n -элементного множества существует взаимно однозначное соответствие. Т.е. порождение подмножеств множества S ={ s 1, s 2,..., sn } эквивалентно порождению n -разрядных двоичных наборов.
Наиболее прямым способом порождения всех двоичных наборов длины n является счет в системе счисления с основанием 2, что реализует алгоритм представленный на рис.2.3.
В алгоритме 1 двоичные наборы длины n формируются в ячейках
(bn -1, bn -2,..., b 0), ячейка bn принимает значение 1, когда все 2 n наборов выданы. Т.е. замечание 1 учтено тем, что при выборе начальной конфигурации инициализируется нулем n +1 ячеек памяти.
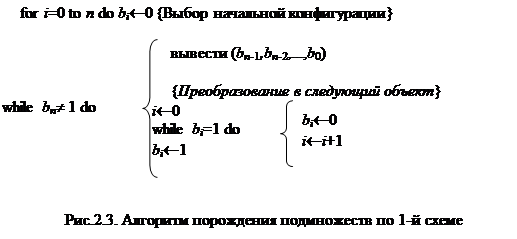 |
Задача порождения случайного подмножества сводится к задаче порождения случайного двоичного набора длины n. Она решается путем генерации случайного числа от 0 до 2 n -1 и обращением его двоичного представления в набор (bn -1, bn -2,..., b 0). Обращение осуществляется с помощью битовых операций сдвига и не является трудоемким.
Использовать данное обращение можно и при порождении всех двоичных наборов, как в алгоритме представленном на рис. 2.4.
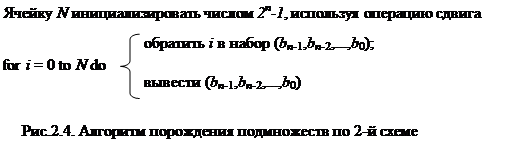 |
Другим комбинаторным объектам также соответствуют целые числа, но процесс обращения для них уже будет достаточно долгим. Поэтому далее алгоритмы, основанные на использовании данного обращения, не рассматриваются.
Рассмотрим алгоритм порождения подмножеств в порядке минимального изменения. Минимальным возможным изменением при переходе от одного подмножества к другому является добавлениеили удаление одного элемента множества. В терминах двоичных наборов это означает, что последовательные наборы должны различаться в одном разряде. Такие последовательности двоичных наборов называются кодами Грея; более точно, n -разрядный код Грея есть упорядоченная циклическая последовательность 2 n n -разрядных наборов (кодовых слов), такая, что последовательные слова отличаются в одном разряде.
Пример 3-разрядного кода Грея приведен в табл. 2.2
Коды Грея удобно задавать начальным словом и последовательностью переходов, т.е. упорядоченным списком номеров разрядов (пронумерованных справа налево), которые меняются при переходе от одного кодового слова к другому. Так для приведенного в табл. 2 кода G (3) начальное слово (000), а последовательность переходов будет иметь вид Т 3=1,2,1,3,1,2,1.
Код Грея используется при построении различных преобразователей. Аналоговая величина - код, где он позволяет свести к единица младшего разряда ошибку неоднозначности при считывании информации.
Таблица 2.2
3-разрядный код Грея
| № | КОД | |
| Двоичный В(3) | Грея G(3) | |
Существует много n -разрядных кодов Грея. Рассмотрим так называемый двоично-отраженный код Грея.
Пусть
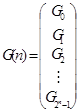
есть n -разрядный код Грея, записанный в форме двоичной 2 n ´ n матрицы так, что 1-я строка матрицы является 1-м кодовым словом - Gi. Дадим рекурсивное определение кода
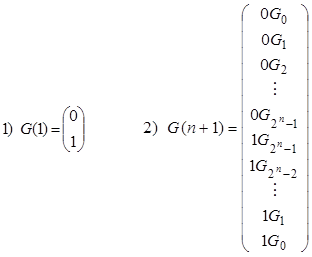 |
Пусть 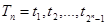 есть последовательность переходов для n -разрядного кода, тогда можно дать рекурсивное определение последовательности переходов.
есть последовательность переходов для n -разрядного кода, тогда можно дать рекурсивное определение последовательности переходов.
1) Т 1=1,
2) Tn +1= Tn, n +1, 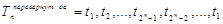 .
.
Следует отметить, что последовательности переходов Tn и 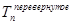 одинаковы (доказывается по индуктивности). Поэтому данное рекурсивное определение упрощается:
одинаковы (доказывается по индуктивности). Поэтому данное рекурсивное определение упрощается:
1) T 1=1,
2) Tn +1= Tn, n +1, Tn.
Итак, для порождения кода Грея достаточно уметь порождать последовательность его переходов. Последовательность переходов можно порождать итеративно, используя стек. Вначале стек содержит элементы n, n -1,...,1 (с 1 в вершине). Затем верхний элемент стека – i выталкивается и помещается в последовательность переходов, после этого в стек добавляются элементы i -1, i -2,...,1. Процесс повторяется пока стек не пуст. Алгоритм порождения кода Грея представлен на рис.2.5.
Для организации стека S можно использовать массив и переменную t, следящую за вершиной стека. Пусть для S отведены ячейки S (1), S (2),..., S (m), тогда пустой стек соответствует случаю t =0, и операции включения x в стек S (обозначение S Ü х) и исключения x из стека S (обозначение х Ü S) будут следующими:
S Ü x tt +1
If t > m then overflow
else S (t) x
x Ü S if t =0 then underflow
else 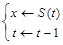
Здесь процедура overflow подразумевает действия, которые необходимо выполнить при переполнении стека, а underflow - при попытке извлечь элемент из пустого стека.
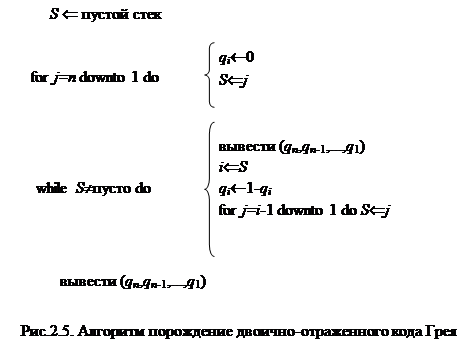 |
 2015-04-01
2015-04-01 2032
2032








