Система состоит из неравенств от двух переменных:
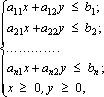
Для решения системы необходимо:
1. Для каждого неравенства выписать уравнение, соответствующее данному неравенству.
2. Построить прямые, являющиеся графиками функций, задаваемых уравнениями.
3. Для каждой прямой определить полуплоскость, которая задается неравенством. Для этого взять произвольную точку, не лежащую на прямой, подставить ее координаты в неравенство. если неравенство верное, то полуплоскость, содержащая выбранную точку, и является решением исходного неравенства. Если неравенство неверное, то полуплоскость по другую сторону прямой является множеством решений данного неравенства.
4. Чтобы решить систему неравенств, необходимо найти область пересечения всех полуплоскостей, являющихся решением каждого неравенства системы.
Эта область может оказаться пустой, тогда система неравенств не имеет решений, несовместна. В противном случае говорят, что система совместна. Решений может быть конечное число и бесконечное множество. Область может представлять собой замкнутый многоугольник или же быть неограниченной.
Пример 3. Решить графически систему: 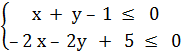
Рассмотрим уравнения x + y–1 = 0 и –2x – 2y + 5 = 0, соответствующие неравенствам. Построим прямые, задающиеся этими уравнениями (Рис. 3).
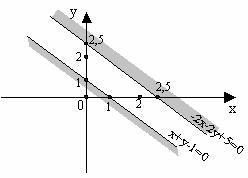
Рисунок 3 – Изображение прямых
Определим полуплоскости, задаваемые неравенствами. Возьмем произвольную точку, пусть (0; 0). Рассмотрим x+ y– 1 ≤ 0, подставим точку (0; 0): 0 + 0 – 1 ≤ 0. значит, в той полуплоскости, где лежит точка (0; 0), x + y – 1 ≤ 0, т.е. полуплоскость, лежащая ниже прямой, является решением первого неравенства. Подставив эту точку (0; 0), во второе, получим: –2 ∙ 0 – 2 ∙ 0 + 5 ≤ 0, т.е. в полуплоскости, где лежит точка (0; 0), –2x – 2y + 5≥ 0, а нас спрашивали, где –2x – 2y + 5 ≤ 0, следовательно, в другой полуплоскости – в той, что выше прямой.
Найдем пересечение этих двух полуплоскостей. Прямые параллельны, поэтому плоскости нигде не пересекаются, значит система данных неравенств решений не имеет, несовместна.
Пример 4. Найти графически решения системы неравенств:
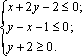
1. Выпишем уравнения, соответствующие неравенствам, и построим прямые (Рис. 4).
x + 2y– 2 = 0 x 2 0
y 0 1
y – x – 1 = 0 x 0 2
y 1 3
y + 2 = 0; y = –2.
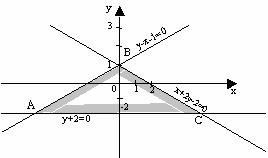
Рисунок 4 – Изображение прямых
2. Выбрав точку (0; 0), определим знаки неравенств в полуплоскостях:
0 + 2 ∙ 0 – 2 ≤ 0, т.е. x + 2y– 2 ≤ 0 в полуплоскости ниже прямой;
0 – 0 – 1 ≤ 0, т.е. y –x– 1 ≤ 0 в полуплоскости ниже прямой;
0 + 2 =2 ≥ 0, т.е. y + 2 ≥ 0 в полуплоскости выше прямой.
3. Пересечением этих трех полуплоскостей будет являться область, являющаяся треугольником. Нетрудно найти вершины области, как точки пересечения соответствующих прямых
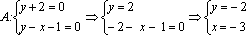
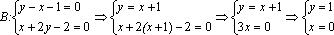
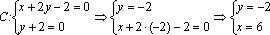
Таким образом, А(–3; –2), В(0; 1), С(6; –2).
Рассмотрим еще один пример, в котором получившаяся область решения системы неограничена.
Пример 5. Решить графически систему 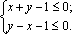
Выпишем уравнения, соответствующие неравенствам, и построим прямые (Рис. 5).
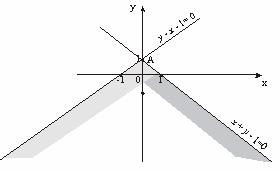
Рисунок 5 – Изображение прямых
x + y – 1 = 0 x 0 1
y 1 0
y – x – 1 = 0 x 0 –1
y 1 0
Определим знаки в полуплоскостях. Выберем точку (0; 0):
0 – 0 – 1 ≤ 0, т.е. y – x – 1 ≤ 0 ниже прямой;
0 + 0 – 1 ≤ 0, т.е. x + y – 1 ≤ 0 ниже прямой.
Пересечением двух полуплоскостей является угол с вершиной в точке А(0;1). Эта неограниченная область является решением исходной системы неравенств.
 2015-04-06
2015-04-06 3795
3795
