Графический метод решения задач линейного программирования

Если задача содержит только две переменные, ее целесообразно решать графическим методом, представляя все условия задачи на графике. Все остальные задачи могут быть решены графически, если есть возможность привести их к задаче, содержащей две неизвестные величины.

Решение задачи графически выполняется в два этапа: построение множества планов (области допустимых решений) и нахождение оптимального плана.

При построении области допустимых решений могут встретиться три случая:

- Множество планов пусто (нет решения);

- Множество планов представляет собой выпуклый ограниченный многоугольник (задача имеет оптимальное решение: единственное или бесчисленное множество);

- Множество планов представляет собой выпуклый неограниченный многоугольник (может иметь или не иметь решения)

Пример.

Предприятие может производить продукцию двух видов. Требуется определить план выпуска продукции каждого вида, обеспечивающий максимально возможную прибыль, если в трех цехах А, Б и В установлено соответственно 24, 15 и 8 единиц оборудования. Прибыль, получаемая предприятием при реализации единицы продукции первого вида, равна 1 руб., а при реализации единицы продукции второго вида 2 руб.

Цех	Норма использования оборудования для производства за 1 ч единицы продукции
Первого вида	Второго вида
А Б В	-

Нормы использования оборудования для производства за 1 ч единицы продукции представлены в таблице.

В цехе В, как видим, продукция первого вида не производится.

В качестве переменных примем:

х₁— объем производства за 1 ч продукции первого вида;

х₂ — объем производства за 1 ч продукции второго вида.

1. Составляем общий вид целевой функции.

Целевая функция определяет величину получаемой прибыли (размер прибыли зависит от объема вырабатываемой продукции):

L(X) = х₁ + 2х₂ ® max

2.Составляем ограничительные уравнения.

Объем вырабатываемой продукции зависит от количества заправленного оборудования.

По первому цеху, например, 2х₁ — планируемое использование оборудования для производства продукции первого вида; Зх₂— планируемое использование оборудования для производства продукции второго вида и (2х₁ + 3х₂) — планируемое использование оборудования для производства всей продукции по первому цеху.

Поскольку планируемое количество используемого оборудования по технологическим переходам не должно превышать его наличия, ограничивающее условие по использованию оборудования первого цеха можно записать так:

2х₁ + 3х₂ £ 24

Аналогично по второму цеху имеем

х₁ + 3х₂ £ 15

По третьему цеху

2х₂ £ 8

Отдельные виды продукции или планируются к выпуску, или не планируются; поэтому искомые переменные могут принимать значения либо большие нуля, либо равные нулю, т. е.

х₁ ³ 0; х₂³ 0

Таким образом, требуется найти значения переменных, которые удовлетворяют следующей системе неравенств:

2х₁ + 3х₂ £ 24

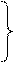х₁ + 3х₂ £ 15

2х₂ £ 8

3. Изображение системы ограничений в прямоугольной системе координат.

По оси абсцисс будем откладывать х₁ — объем производства продукции первого вида, а по оси ординат х₂ — объем производства продукции второго вида.

Проведем на графике прямую, соответствующую уравнению 2х₁ + 3х₂ = 24,

которое получено из первого неравенства системы ограничений. Для этого отыщем две точки, в которых прямая будет пересекать оси координат.

В точке пересечения с осью ординат х₁ = 0 и, следовательно из уравнения, х₂ = 8. В точке пересечения с осью абсцисс х₂ = 0 и х₁ = 12.

Отметив на осях точки х₁ = 12 и х₂ = 8, соединим их и получим исходную прямую.

4.Определение полуплоскости допустимых значений.

Прямая делит плоскость на две полуплоскости, причем точки, координаты которых удовлетворяют неравенству 2х₁ + 3х₂ < 24, лежат в одной полуплоскости, а точки, координаты которых удовлетворяют неравенству 2х₁ + 3х₂ > 24, лежат в другой полуплоскости.

Чтобы определить, какая из полуплоскостей соответствует, предположим, неравенству 2х₁ + 3х₂ < 24, необходимо взять произвольную точку на плоскости и ее координаты подставить в неравенство. Если при этом окажется, что неравенство выполнено, то эта и любая другая точка рассматриваемой полуплоскости удовлетворяют этому неравенству, и наоборот.

Так как для проверки берется произвольная точка, проще всего брать точку с координатами (0; 0). Подставим координаты точки (0; 0) в неравенство 2х₁ + 3х₂ < 24; получаем 2*0 + 3*0<24, т. е. точка (0; 0), как и все точки полуплоскости, которая содержит эту точку, удовлетворяет неравенству 2х₁ + 3х₂ < 24.

5. Определение полуплоскости для других неравенств.

Для второго неравенства х₁ + 3х₂ £ 15.

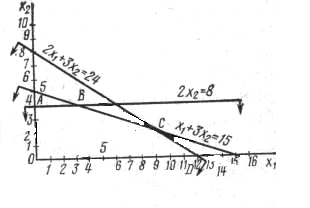Прежде всего нанесем на график прямую х₁ + 3х₂ = 15, делящую плоскость на две полуплоскости. Эта прямая пересекает оси координат в точках х₁ = 15 и х₂ = 5. Далее подставим координаты точки (0; 0) в неравенство х₁ + 3х₂ £ 15; получаем 0 + 3х0£15. Следовательно, полуплоскость, содержащая точку (0; 0), является допустимой для неравенства х₁ + 3х₂ £ 15.

Проведя аналогичные рассуждения при анализе неравенства 2х₂£8, убеждаемся, что этому неравенству удовлетворяют точки нижней полуплоскости вместе с ее граничными точками — точками прямой 2х₂ = 8.

6. Определение допустимого множества решений.

План выпуска изделий должен определяться с учетом выполнения условий х₁ ³ 0 и х₂³ 0, а это означает, что допустимое множество значений переменных может лежать только в первом квадранте.

Это допустимое множество изображено на рисунке и представляет собой многоугольник OABCD. В пределах этого многоугольника любая программа выпуска продукции х₁ и х₂ является допустимой.

7. Определение оптимального решения (максимума).

Из всех допустимых вариантов плана производства нужно выбрать такой, который обеспечивает наибольшую прибыль т. е. приводит к максимуму величину L(X) = х₁ + 2х₂.

Если L придать определенное числовое значение, то полученное уравнение можно также изобразить на графике. Изменяя значение L, можно получить семейство прямых, параллельных первой прямой, но отстоящих дальше или ближе от начала координат.

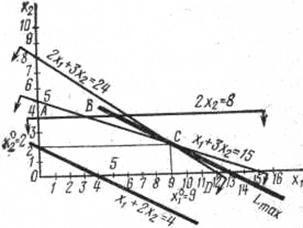Обычно оптимальное решение находится на пересечении прямой L с одной из вершин области допустимых значений переменных (в этом случае мы имеем единственное оптимальное решение).

Если же прямая L совмещается с гранью многоугольника решений, то можно найти множество оптимальных решений, имеющих одинаковое значение целевой функции.

Пусть L₁ = 4. Проведем на графике прямую х₁ + 2х₂=4; она пересечет оси координат в точках х₁ = 4 и х₂=2. Точки, лежащие на этой прямой, отвечают планам производства, обеспечивающим за час 4 руб. прибыли. Программы, обеспечивающие, к примеру, 6 руб. прибыли за час, будут представлены на графике точками прямой х₁ + 2х₂= 6, удаленной на большее расстояние от начала координат.

Для нахождения программы выпуска продукции, обеспечивающей наибольшую прибыль, нужно построить прямую, наиболее удаленную от начала координат, но имеющую хотя бы одну общую точку с областью допустимых значений переменных х₁ и х₂. Такой прямой является прямая, проходящая через точку С. Следовательно, точка С является допустимым решением, обеспечивающим наибольшую прибыль.

8. Определим координаты точки С.

Эта точка образована пересечением прямых 2х₁ + 3х₂ = 24 и х₁ + 3х₂ =15. Решая систему двух уравнений, находим оптимальное решение задачи: х₁ = 9, х₂ = 2.

9. Решение.

Подставляя найденные значения в целевую функцию, находим

L_max = 9 + 2*2=13.

10. Вывод.

Таким образом, чтобы получить максимальную прибыль в размере 13 руб. за час, необходимо запланировать производство девяти единиц продукции первого вида и двух единиц продукции второго вида.