I) Неравенства вида 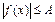 решаются следующим образом.
решаются следующим образом.
Если 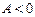 , то решений нет
, то решений нет
Если 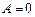 , то
, то 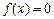
Если 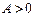 , то неравенству
, то неравенству 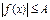 равносильна система
равносильна система 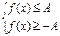
II) Неравенства вида 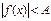 решаются следующим образом.
решаются следующим образом.
Если 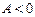 , то решений нет
, то решений нет
Если 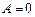 , то решений нет
, то решений нет
Если 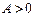 , то неравенству
, то неравенству 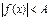 равносильна система
равносильна система 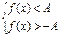
III) Неравенства вида 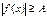 решаются следующим образом.
решаются следующим образом.
Если 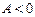 , то неравенство верно для любых х из области определения
, то неравенство верно для любых х из области определения 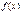
Если 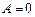 , то неравенство верно для любых х из области определения
, то неравенство верно для любых х из области определения 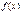
Если 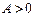 , то неравенству
, то неравенству 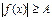 равносильна совокупность
равносильна совокупность 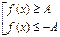
IV) Неравенства вида 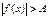 решаются следующим образом.
решаются следующим образом.
Если 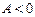 , то неравенство верно для любых х из области определения
, то неравенство верно для любых х из области определения 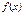
Если 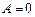 , то неравенству
, то неравенству 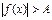 равносильна система
равносильна система 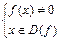
Если 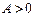 , то неравенству
, то неравенству 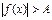 равносильна система
равносильна система 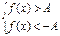
V) Неравенства вида 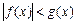 решаются следующим образом.
решаются следующим образом.
Если 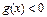 , то решений нет.
, то решений нет.
Если 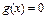 , то решений нет.
, то решений нет.
Если 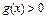 , то неравенству
, то неравенству 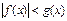 равносильна система
равносильна система 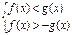
VI) Неравенства вида 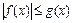 решаются следующим образом.
решаются следующим образом.
Если 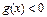 , то решений нет.
, то решений нет.
Если 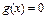 , то неравенству
, то неравенству 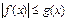 соответствует уравнение
соответствует уравнение 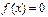
Если 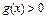 , то неравенству
, то неравенству 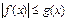 равносильна система
равносильна система 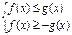
VII) Неравенства вида 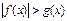 решаются следующим образом.
решаются следующим образом.
Если 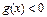 , то неравенство
, то неравенство 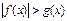 верно для любых значений x из области определения неравенства
верно для любых значений x из области определения неравенства 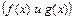
Если 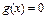 , то неравенству
, то неравенству 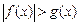 равносильна система
равносильна система 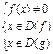
Если 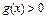 , то неравенству
, то неравенству 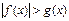 равносильна совокупность
равносильна совокупность 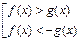
VIII) Неравенства вида 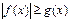 решаются следующим образом.
решаются следующим образом.
Если 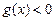 , то неравенство
, то неравенство 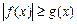 верно для любых значений x из области определения неравенства
верно для любых значений x из области определения неравенства 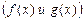
Если 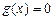 , то неравенство
, то неравенство 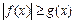 верно для любых значений x из области определения неравенства
верно для любых значений x из области определения неравенства 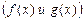
Если 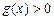 , то неравенству
, то неравенству 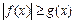 равносильна совокупность
равносильна совокупность 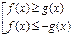
IX) Неравенства вида 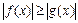 и
и 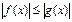 решаются следующим образом.
решаются следующим образом.
Неравенству 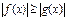 соответствует неравенство
соответствует неравенство 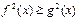
Неравенству 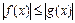 соответствует неравенство
соответствует неравенство 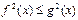
 2015-03-22
2015-03-22 388
388







