а) Если при вычислении предела получена неопределенность вида 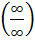 , то для ее раскрытия нужно и числитель и знаменатель дроби разделить на наибольшую, входящую в них степень аргумента:
, то для ее раскрытия нужно и числитель и знаменатель дроби разделить на наибольшую, входящую в них степень аргумента:
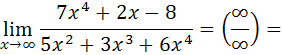
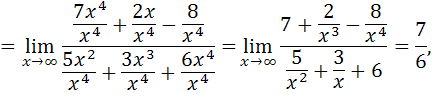
так как
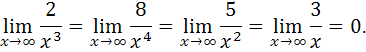
б)
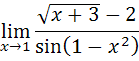
В данном случае при 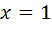 и числитель, и знаменатель дроби обращаются в 0, то есть получается неопределенность вида
и числитель, и знаменатель дроби обращаются в 0, то есть получается неопределенность вида 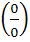 . Для раскрытия неопределенности избавимся от иррациональности, умножив и числитель и знаменатель дроби на сопряженное выражение, а также воспользуемся первым замечательным пределом:
. Для раскрытия неопределенности избавимся от иррациональности, умножив и числитель и знаменатель дроби на сопряженное выражение, а также воспользуемся первым замечательным пределом:
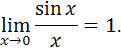
Получим:
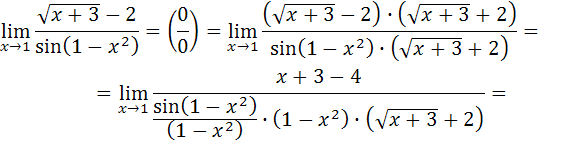
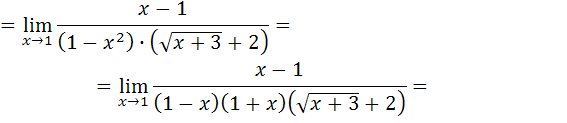
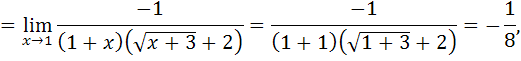
так как
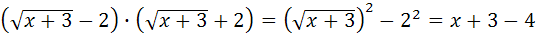
и
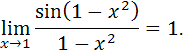
в)
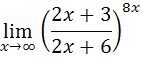
При 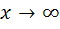 получаем неопределенность вида
получаем неопределенность вида 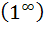 , раскрыть которую можно воспользовавшись вторым замечательным пределом:
, раскрыть которую можно воспользовавшись вторым замечательным пределом:
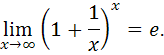
Выделяя структуру второго замечательного предела, получим:
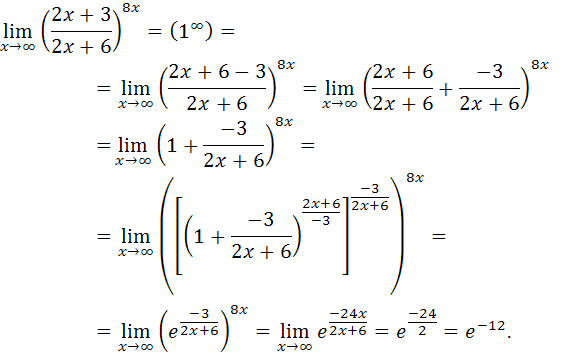
2. Найти точки разрыва функции и указать их характер.
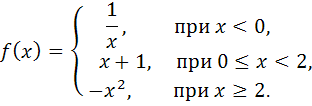
Функция определена на всей числовой оси, т.е. 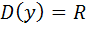 ,
,
поэтому разрыв возможен только в точках 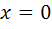 и
и 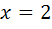 .
.
1) Пусть 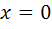 . Тогда:
. Тогда:
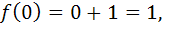
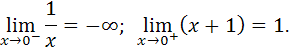
Предел функции в точке 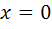 слева равен бесконечности и, следовательно, точка
слева равен бесконечности и, следовательно, точка 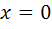 является точкой разрыва второго рода.
является точкой разрыва второго рода.
2) Пусть 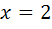 . Тогда:
. Тогда:
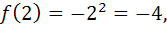
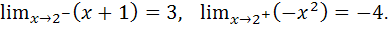
Односторонние пределы функции в точке 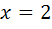 конечны, но не равны. Следовательно, точка
конечны, но не равны. Следовательно, точка 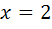 является точкой разрыва первого рода, а именно точкой скачка функции.
является точкой разрыва первого рода, а именно точкой скачка функции.
3. Полное исследование функции проводится по следующей схеме:
1) область определения, область значений функции;
2) четность, нечетность функции, периодичность;
3) асимптоты;
4) промежутки монотонности и точки экстремума;
5) промежутки выпуклости и вогнутости графика функции, точки перегиба;
6) точки пересечения графика функции с осями координат;
7) построение графика.
Например:
а) найти асимптоты графика функции 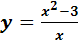 .
.
Решение.
1) Функция 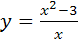 не определена в точке
не определена в точке 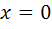 . Найдем односторонние пределы функции в этой точке:
. Найдем односторонние пределы функции в этой точке:

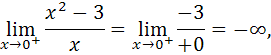
значит, прямая 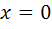 является вертикальной асимптотой.
является вертикальной асимптотой.
2) Найдем
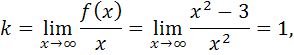
значит, функция имеет наклонную асимптоту 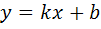 , где
, где
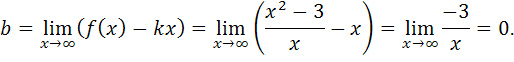
Таким образом, наклонной асимптотой графика функции 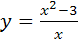 является прямая
является прямая 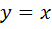 .
.
б) Найти промежутки монотонности и точки экстремума функции 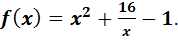
Решение.
1) Найдем производную:
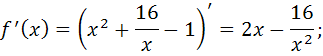
2) определим точки, в которых выполняется необходимое условие экстремума, решив уравнение 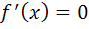 :
:
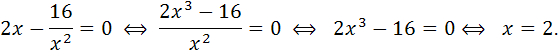
При 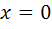 производная не существует.
производная не существует.
Точки 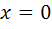 и
и 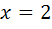 разбивают числовую ось на интервалы
разбивают числовую ось на интервалы 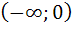 ,
, 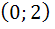 и
и 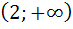 .
.
3) Определим знак производной на полученных промежутках:
| Промежуток | 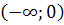 | 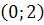 | 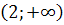 |
| Производная | 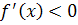 | 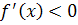 | 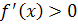 |
Таким образом, при 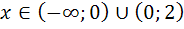 функция убывает, а при
функция убывает, а при 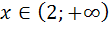 − возрастает. Точка
− возрастает. Точка 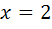 является точкой минимума функции. При этом минимальное значение функции равно
является точкой минимума функции. При этом минимальное значение функции равно
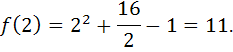
в) Найти промежутки выпуклости (вогнутости) и точки перегиба графика функции 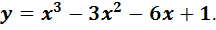
Решение.
1) Найдем производную второго порядка:
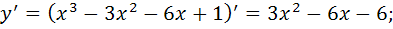
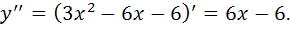
2) Найдем точки, в которых выполняется необходимое условие перегиба, решив уравнение 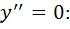
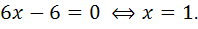
Точка 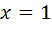 разбивает числовую ось на два интервала:
разбивает числовую ось на два интервала: 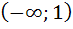 и
и 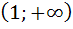 .
.
3) Определим знак второй производной на полученных промежутках:
| Промежуток | 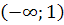 | 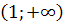 . . |
| Производная второго порядка | 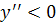 | 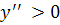 |
Таким образом, при 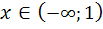 график функции выпуклый вверх, а при
график функции выпуклый вверх, а при 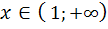 − выпуклый вниз (вогнутый).
− выпуклый вниз (вогнутый).
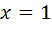 − точка перегиба, в которой значение функции равно
− точка перегиба, в которой значение функции равно 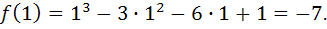
 2015-04-08
2015-04-08 32223
32223
