Политропный процесс

Все рассмотренные выше процессы обладают одной общей особенностью – они происходят при постоянной теплоемкости С

при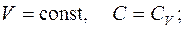

при 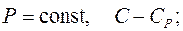(6.41)

при

при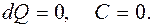

Процессы, в которых теплоемкость постоянна, называют политропными. Все изопроцессы, включая адиабатический, являются частными случаями политропного процесса.

Аналогично выводу уравнения адиабаты (6.37), используя первое начало термодинамики и уравнение Менделеева – Клапейрона для 1 моля,

получим

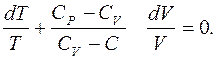(6.42)

Интегрируя выражение (6.42), получим уравнение политропы

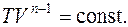(6.43)

Заменив в (6.43) температуру T соотношением, полученным из уравнения Менделеева – Клапейрона, как 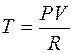, получим

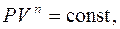(6.44)

где 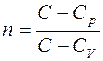– показатель политропы.

При 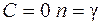получим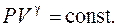

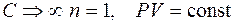– уравнение изотермы;

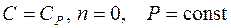– уравнение изобары; (6.45)

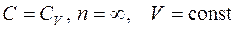– уравнение изохоры.