Оценка существенности связи. Принятие решений на основе уравнения регрессии

Проверка адекватностей моделей построенных на основе уравнений регрессии, начинается с проверки значимости каждого коэффициента регрессии. Критерии существенности связи основываются на нормальном распределении признака в исследуемой совокупности.

Значимость коэффициента регрессии осуществляется с помощью t-критерия Стьюдента (при n<30):

Для параметра а

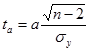
где n-число единиц совокупности

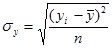-среднее квадратическое отклонение результативного признака y_i от выровненных значений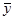

Для параметра b

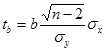
где 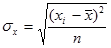среднее квадратическое отклонение факторного признака х_i от общей средней .

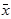Параметр модели признается статистически значимым, если t_р>t_кр(определяется по таблице Стьюдента при соответствующем числе степеней свободы и уровня значимости, число степеней свободы n=n-k, где к -число параметров в уравнении регрессии; n - число единиц в совокупности.

Теснота связи между признаками оценивается, как правило, на основе ограниченной информации об изучаемом явлении, полученной при выборочном наблюдении. Поэтому для распространения выводов по результатам выборки на генеральную совокупность необходима оценка существенности коэффициента регрессии.

Оценка существенности линейного коэффициента корреляции дают возможность распространить выводы по результатам выборки на генеральную совокупность. В зависимости от объема выборочной совокупности и величины коэффициента корреляции предлагаются различные методы оценки его существенности. В основу критериев положен закон нормального распределения значений признака в генеральной совокупности.

При малых объемах выборки для проверки гипотезы об отсутствии корреляционной связи применяется критерий Стьюдента t. Расчетная величина t-критерия 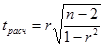распределена по закону Стьюдента с (п - 2) степенями свободы.

Полученную величину t _расч сравнивают с табличным значением t-критерия (число степеней свободы равно п - 2 и при соответствующем уровне значимости).

Если t_расч³t_k то величина коэффициента корреляции признается существенной, а это значит, что связь между признаками существует. Если t_расч<t_k, то полагают, что связь между признаками носит случайный характер.

Применим указанный метод к оценке существенности корреляции между уровнем затрат туристических фирм на рекламу и числом туристов, воспользовавшихся услугами фирм. При объеме выборки, равном 20, и при условии, что величина коэффициента корреляции равна 0,8105

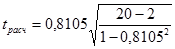=5,872

В таблице для числа степеней свободы к=n - 2 = 18 и уровня значимости 1% находим, что t = 2,878 (см. Приложение 4).

Т. о. можно считать с вероятностью 99%, что в генеральной совокупности действительно существует прямая зависимость между изучаемыми признаками.

При большом объеме выборки распределение линейного коэффициента корреляции можно считать приближено нормальным со средней r и дисперсией 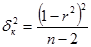, где r линейный коэффициент корреляции, n- объем совокупности.

Средней квадратической ошибкой коэффициента корреляции и определяется по формуле: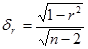

Если коэффициент корреляции r больше 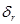в t_a раз, т.е. 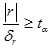, то можно говорить о существенности выборочного коэффициента корреляции. Если 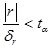, то с вероятностью (1-a) можно предполагать отсутствие корреляционной связи в генеральной совокупности (уровень значимости a=0,01 или 0,05; ему соответствует t_a=2,58 или 1,96).

В тех случаях, когда линейный коэффициент корреляции, полученный по данным относительно малой выборки, близок к единице (r> 0,8), распределение его оценок отличается от нормального распределения или распределения Стьюдента. В таких случаях для проверки его существенности рекомендуется использовать метод преобразованной корреляции, предложенный Р. Фишером.

Р. Фишер показал, что распределение логарифмической функции линейного коэффициента корреляции (обозначается эта функция через Z) приближается к нормальной кривой даже для выборок очень небольшого объема:

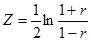
Средняя квадратическая ошибка Z-распределения зависит только от объема выборки и определяется по формуле:

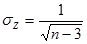
По таблице соотношений между г и Z (см. Приложение 7), дающей возможность избежать вычислений логарифмов, находим, что коэффициенту корреляции 0,8105 соответствует Z = 1,13. Для числа наблюдений п = 20:

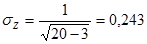
Отношение Zк средней квадратической ошибке s₂ равно 4,65 (1,13:0,243). Поскольку отношение Z/ 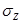оказалось больше табличного значения критерия Стьюдента при уровне значимости 1%, можно полагать действительное наличие связи между признаками в генеральной совокупности.