Если вещество поместить в магнитное поле, микротоки будут определенным образом ориентироваться в пространстве 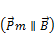 . В вакууме мы имели теорему о циркуляции вектора магнитной индукции:
. В вакууме мы имели теорему о циркуляции вектора магнитной индукции:
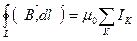
В веществе:
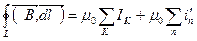
Второе слагаемое – сумма атомных микротоков.
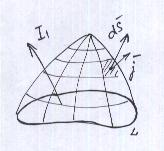
Для вычисления этой суммы рассмотрим достаточно малый отрезок замкнутого контура в веществе (на рисунке 27 показана лишь часть контура L)
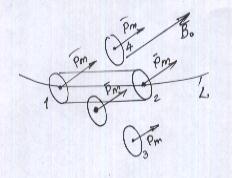
Если вещество находится во внешнем поле, магнитные моменты микротоков ориентированы параллельно 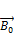 . Можно убедиться в том, что вклад в циркуляцию вектора
. Можно убедиться в том, что вклад в циркуляцию вектора 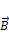 по контуру L дадут только токи, «нанизывание» на контур. Ток 4 в плоскость контура входит и входит, их алгебраическая сумма равна 0. Микроток 3 вообще лежит вне контура, токи 2 и 1 входят в контур, а выходят уже вне контура, то есть они и дадут вклад во второе слагаемое формулы 1. Первое слагаемое - это макротоки, входящие в контур L.
по контуру L дадут только токи, «нанизывание» на контур. Ток 4 в плоскость контура входит и входит, их алгебраическая сумма равна 0. Микроток 3 вообще лежит вне контура, токи 2 и 1 входят в контур, а выходят уже вне контура, то есть они и дадут вклад во второе слагаемое формулы 1. Первое слагаемое - это макротоки, входящие в контур L.
Чтобы подсчитать число «нанизанных» токов, делают построение: строится косой цилиндр.(см. рис.) Если центр микротока (ядро атома) попадает в цилиндр, то этот ток «нанизан» на контур и он учитывается. Сумма микротоков 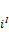 на отрезке dl:
на отрезке dl:
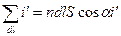
 ,
, 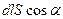 -объем косого цилиндра
-объем косого цилиндра
n – концентрация вещества (число атомов в единице объема)
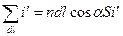 .
. 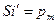 ,
, 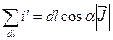 ;(
;(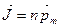 )
)
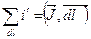
 Формулу (1) можно переписать в следующем виде:
Формулу (1) можно переписать в следующем виде:

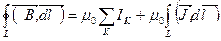
Разделим все на 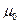 и перенесём все в одну строку:
и перенесём все в одну строку:
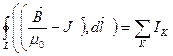
Напрашивается шаг – ввести новый вектор 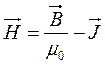 . Он называется напряжённость магнитного поля [
. Он называется напряжённость магнитного поля [ 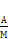 ]
]
Для вакуума 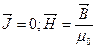 . Поэтому:
. Поэтому:
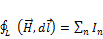
Или
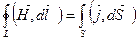
S – любая поверхность, опирающаяся на контур L.
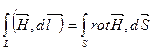
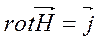 ;
; 
 2015-04-20
2015-04-20 1694
1694








