Неизвестными параметрами являются площади поперечных сечений стержней А1 и А2 и угол 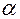 . Целевая функция задачи – объем материала:
. Целевая функция задачи – объем материала:

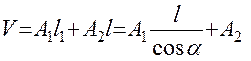 . (5.1)
. (5.1)
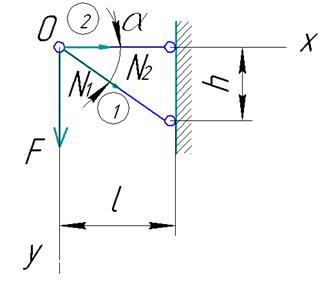 Направим реакции N1 и N2 в стержнях от узла. Определим из условий равновесия для сходящейся системы сил рекции в стержнях:
Направим реакции N1 и N2 в стержнях от узла. Определим из условий равновесия для сходящейся системы сил рекции в стержнях:
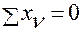 ;
; 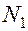
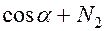
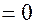 ;
;
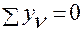 ;
; 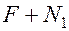
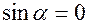 ;
;
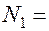
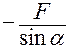 ;
;
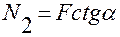 .
.
Рис. 5.1. Расчетная схема двухстержневого кронштейна
Знак «–» показывает, что истинное направление реакции N1 противоположно выбранному.
Ограничениями являются условия прочности стержней:
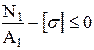 ,
, 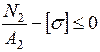 , (5.2)
, (5.2)
или
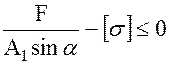 ,
, 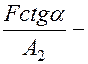
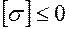 , (5.3)
, (5.3)
и конструктивное ограничение 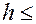 1,5 l, т.е. tg
1,5 l, т.е. tg 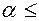 1,5, что соответствует
1,5, что соответствует 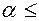
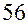 ,
, 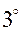 . Последнее неравенство определяет допустимую область проектирования (рис. 5.2).
. Последнее неравенство определяет допустимую область проектирования (рис. 5.2).
Решая уравнения (5.2 и 5.3) относительно 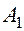 и А2, находим:
и А2, находим: 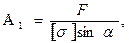
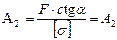
Целевая функция примет вид: 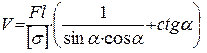 .
.
Исследуя на экстремум последнее выражение, взяв производную от него по параметру 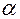 и приравняв к нулю, получим cos
и приравняв к нулю, получим cos 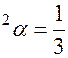 откуда,
откуда, 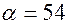 ,
, 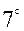 .
.
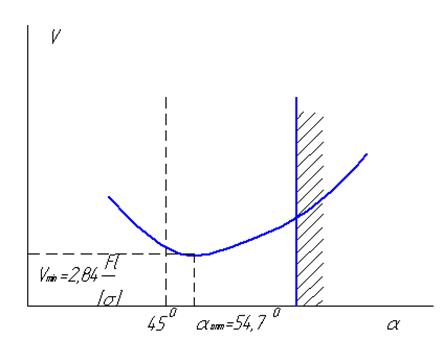
α=56,30
Рис. 5.2. Графическое решение задачи
На рис. 5.2 показан график зависимости целевой функции V от параметра 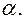
 Область допустимых решений ограничена линией
Область допустимых решений ограничена линией 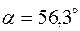 . Минимум функции V находится в этой области.
. Минимум функции V находится в этой области.
Если бы в качестве конструктивного ограничения было задано ограничение 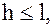 то оптимальному решению соответствовало бы значение параметра
то оптимальному решению соответствовало бы значение параметра 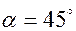 .
.
 2015-04-30
2015-04-30 307
307








