2015-04-30
438
Если на поверхности призматического стержня нанести сетку линий, параллельных и перпендикулярных оси стержня (рис. 7а), и приложить к нему растягивающую силу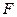 
(рис. 7б), то можно убедиться в том, что линии сетки после деформации останутся взаимно перпендикулярными. 
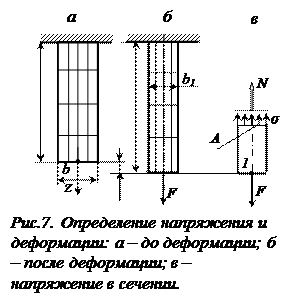
Можно предположить, что и внутри стержня будет такая же картина, т. е. поперечные сечения стержня, плоские и нормальные к его оси до деформации, останутся плоскими и нормальными к оси и после деформации. Эта гипотеза называется гипотезой плоских сечений или гипотезой Бернулли. Формулы, полученные на основе этой гипотезы, подтверждаются результатами опытов.
Такая картина деформаций позволяет считать, что в поперечных сечениях стержня действуют только нормальные напряжения, равномерно распределённые по сечению, а касательные – равны нулю.
Продольная сила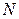 
– равнодействующая нормальных напряжений в поперечном сечении:
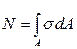. (2.1)
Так как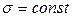 
(по гипотезе Бернулли), то
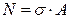, (2.2)
откуда
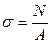, (2.3)
где А – площадь сечения стержня.
Эта формула справедлива и при сжатии, с той лишь разницей, что сжимающее напряжение считается отрицательным.
