Ранговыми коэффициентами связи называются меры связи, позволяющие вычислять степень согласованности в ранжировании одних и тех же объектов по двум различным основаниям или по двум различным признакам. Мы неоднократно ссылались на необходимость для социолога такого рода коэффициентов. Например, при построении шкалы суммарных оценок появлялась необходимость в проверке согласованности результатов, полученных по итоговой шкале, с данными по исходным шкалам (суждениям).
Коэффициентов ранговой корреляции много. Для того чтобы понять их схожесть и различие, необходимо вначале несколько отойти от таблиц сопряженности и нашей задачи. А вам придется вернуться к разделу книги, посвященному процедуре ранжирования. Как было отмечено, такая процедура возникает у социолога как на этапе измерения, так и на этапе анализа данных. В любом случае возникает задача определения степени согласованности двух ранжированных рядов. Представим себе, что для одной и той же совокупности объектов получили два ранжированных ряда. Например, по тем же будущим профессиям студента. Значит, объектов у нас всего шесть по числу профессий. Пусть первый ряд получен по степени уменьшения индекса удовлетворенности учебой. Второй ряд ¾ по степени уменьшения индекса уверенности в трудоустройстве по профессии после окончания вуза. Далее будем коротко называть эти признаки — «удовлетворенность» и «уверенность».
В данном контексте мы не будем обсуждать вопрос, каким образом измерены эти признаки как характеристики группы. Заметим лишь, что они могли быть получены с помощью шкалы суммарных оценок или как групповые индексы, примеры которых были приведены в «Лекциях».
В случае полной (максимальной) согласованности ранжирования по этим двум признакам естественно предположить наличие тесной (сильной) связи между признаками «удовлетворенность» и «уверенность». Такая связь может быть и прямой (чем больше удовлетворенность, тем больше уверенность), и обратной (чем больше удовлетворенность, тем меньше уверенность). Из этого проистекает, что логично изменяться значениям коэффициента ранговой корреляции от -1 до +1. Этим свойством обладают все приведенные ниже коэффициенты.
Приведем примеры нескольких коэффициентов, а затем поясним их содержательный смысл.
Мера g (гамма) Л. Гудмена и Е. Краскала (L.Goodman, E.Kraskal)

Первая из этих мер в работе [8, с. 135], обозначена как «g Гудмана». Эти меры удачно описаны в работе [1, с. 37—40]. Вы, конечно, обратили внимание, что у всех приведенных мер один и тот же числитель, а знаменатели различны. Прежде всего рассмотрим числитель, ибо он несет в себе основное содержание коэффициентов, В таблице 3.5.4 представлены два ранжированных ряда. Объекты ранжирования¾ будущие профессии. Они приведены в таблице для удобства в том порядке, в котором их ранги во втором ряду возрастают, т. е. в порядке убывания степени уверенности. Число рангов равно числу объектов, связанных рангов (одинаковых) в наших рядах не наблюдается.
Таблица 3.5.4
Примеры двух ранжированных рядов
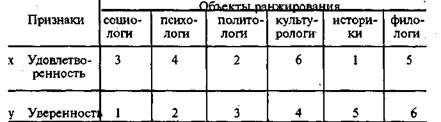
Из этой таблицы видим, что политологи в первом ряду имеют ранг 2, а во втором ¾ ранг 3, а историки в первом ряду ¾ ранг 1, во втором ¾ ранг 5. Для того чтобы оценить степень согласованности наших, грубо говоря, «ранжировок», можно применить тот же прием, который был применен при вычислении меры качественной вариации. Образуем из наших шести объектов различные пары. Таких пар будет 6x5/2=15. Возьмем отдельную пару объектов. Ранги, соответствующие первому объекту, обозначим (i1, j1), а второму ¾ (i2, j2). Эти ранги могут находиться в различных отношениях. Возможна одна из двух ситуаций, каждая из которых включает два возможных соотношения между рангами (1а, 16, 2а, 26).

В первой ситуации ранги как бы согласованы, а во втором не согласованы. Подсчитаем, для скольких пар из 15-ти наблюдается согласованность, и обозначим число таких пар через S. Затем подсчитаем, для скольких пар наблюдается несогласованность, и обозначим число таких пар через D. В числителе всех приведенных выше мер стоит как раз разница между числом согласованных и несогласованных пар объектов. Для примера наших ранжированных рядов величина (S-D) равна:
S-D = (3-2) + (2-2) + (2-1) + (0-2) + (1-0) = 1.
Здесь первая скобка ¾ результат анализа согласованности / несогласованности рангов в парах, образованных первым объектом с остальными пятью, т. е. в парах (1 и 2), (1 и З), (1 и 4), (1 и 5), (1 и 6). Среди них согласованность (случай 1а) — в трех парах, а несогласованность (случай 26) — в двух парах. Вторая скобка ¾ результат анализа пар, образованных вторым объектом, т. е. пар (2 и 3), (2 и 4), (2 и 5), (2 и 6). Среди них в двух парах согласованность, а в двух ¾ несогласованность. Последняя скобка ¾ результат анализа пары (5 и 6).
Мы рассматривали случай отсутствия связанных рангов, поэтому для определения степени согласованности можно использовать первый из трех коэффициентов, приведенных выше. Знаменатель для его вычисления равен:
S+D = (3+2) + (2+2) + (2+1) + (0+2) + (1+0) = 15
или просто числу различных возможных пар, т. е. 6x5/2=15
Тогда g» 0,07. В самом деле степень согласованности в наших ранжированных рядах очень мала. Второй из трех коэффициентов учитывает наличие связанных рангов. Кроме соотношений (1а; 1б;
 Число пар, соответствующих третьей ситуации (есть связанные ранги во втором ряду), обозначим через Ту. Число пар, соответствующих четвертой ситуации (есть связанные ранга в первом ряду), обозначим через Тх. Второй коэффициент учитывает число связанных рангов в том и другом ранжированных рядах.
Число пар, соответствующих третьей ситуации (есть связанные ранги во втором ряду), обозначим через Ту. Число пар, соответствующих четвертой ситуации (есть связанные ранга в первом ряду), обозначим через Тх. Второй коэффициент учитывает число связанных рангов в том и другом ранжированных рядах.
И наконец, обратите внимание на коэффициент dy/x. Мер Сомерса всего три по аналогии с мерами «лямбда» Гуттмана и «гамма» Гудмена и Краскала, т. е. ранговые коэффициенты связи бывают и направленные. Мы привели только одну из трех мер Сомерса. В случае ее использования вопрос о степени согласованности в ранжированных рядах звучит несколько иначе, а именно: влияет ли «уверенность» на «удовлетворенность» и, наоборот, влияет ли ранжирование по «удовлетворенности» на ранжирование по «уверенности». Разумеется, только в смысле того, что ранжирование объектов по степени убывания «удовлетворенности» (признак У) зависит от ранжирования по степени убывания «уверенности» (признак X). Поэтому в знаменателе учитываются связанные ранги только для признака У.
А теперь представим себе, что речь идет об анализе связи по таблице сопряженности (корреляционная таблица) двух признаков, имеющих порядковый уровень измерения. Допустим, что у каждого нашего студента-гуманитария есть оценка не только удовлетворенности учебой, но и удовлетворенности собой. Оба признака имеют порядковый уровень измерения. Для изучения связи между ними используются те же ранговые меры связи. Их значения рассчитываются по тем же формулам, ибо можно всех наших студентов (объекты ранжирования) упорядочить и получить два ранжированных ряда. Первый ¾ по степени убывания (возрастания) удовлетворенности учебой, а второй ¾ по убыванию (возрастанию) удовлетворенности собой. Естественно, у нас будут сплошь связанные ранги. Напомним, что число рангов равно числу объектов, т. е. 1000. Реально никто такое ранжирование не проводит, а просто вычисляются по таблице сопряженности число согласованных пар, число несогласованных и число связанных рангов. Существуют коэффициенты ранговой корреляции для быстрого счета (коэффициент Спирмена), но в век компьютеров они уже утратили свою актуальность.
Мы рассмотрели все коэффициенты, необходимые для первоначального понимания того, что они из себя представляют, и почему их так много. В завершение этого раздела книги несколько слов о том, что все эти коэффициенты являются статистиками, т.е. для них можно построить доверительный интервал. Тот интервал, в котором находится истинное значение коэффициента, т. е. для изучаемой генеральной совокупности. Доверительные интервалы есть для «лямбда» [1, с. 34], «may» [1, с. 36], для коэффициентов ранговой корреляции [9, с. 185—187].
В рамках книги не ставилась цель привести все меры или дать их классификацию, ибо для этого необходимы серьезные знания в области науки под названием теория вероятности и математическая статистика. Более того, мы намеренно не рассматривали меры для изучения связи между признаками, измеренными по «метрическим» шкалам (по всем, по которым уровень измерения выше порядкового). Такая позиция обусловлена сочетанием двух факторов процесса обучения студентов. Во-первых, в эмпирической социологии такого рода шкалы встречаются реже других. Во-вторых, в читаемом студентам курсе «Теория вероятности и математическая статистика» понятие «связь» вводится именно с такого рода мер связи.
Смысл РА (регрессионный анализ): РА устанавливает функциональные связи между зависимой переменной (У) и независимыми переменными (Хi), где i принадлежит (1;n), где
Х-входная переменная; регрессор.
У- регрессанд, функция отклика.
Х, У – количественные переменные.
Если i=1, то анализ однофакторный (парная регрессия)
Если i от 2 до n, то многофакторный (множественная регрессия).
Цель применения регрессионного анализа:
· прогнозирование;
· имитация (корректировка Х, изменяя У) вид условной зависимости.
· Определить вклад независимых переменных в вариацию зависимой
· Определение наличия и характера (математического уравнения, описывающего зависимость) связи между переменными
Для обобщения данных строятся таблицы для значений зависимых и независимых переменных. Иногда, можно изобразить графике для наглядного рассеивания, но это е удобно для дальнейшего использования данных, например для оценки модели. Для обобщения данных с помощью программного обеспечения также стояться таблицы, что является более удобным для большой совокупности данных. Под каждой таблицей д.б.суммарные числа, итог.
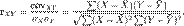 Взаимосвязь переменных оценивается с помощью: корреляционного анализа (определяется теснота связи): от -1 до +1.
Взаимосвязь переменных оценивается с помощью: корреляционного анализа (определяется теснота связи): от -1 до +1.
и с помощью регрессионного анализа непосредственно (определение количественной причинной зависимости): Y = α 0 + α 1 X 1 + α 2 X 2 +... + αNXi + ξ, с помощью МНК – оценка коэффициентов (может быть это прямой анализ).
График рассеивания покажет тесноту связи или отсутствие таковой так же.
Анализ уравнения регрессии:
1. Проверка коэффициентов на значимость. Оценка параметров модели: альфа, проводится для каждого коэффициента.
Н0: αi = 0 – коэффициент НЕ значим.
Н1: αi ≠ 0 – коэффициент значим.
У = α0 + α1*х1 + α2*х2 + α3*х1*х2 + ξ. (х1*х2 – взаимное влияние факторов).
Если коэф.значим, то переменная, которая находится при коэффициенте оказывает влияние на у. Используется для проверки t критерий Стьюдента: если tрасч <tтабл, то Н1 (оказывает влияние).
tтабл (α/2; n-k), где n – число пар наблюдений, к – число параметров модели.
tрасч = модуль α с крышечкой итое делить на корень из сигмы в квадрате с индексом α с крышечкой итое. Сигма квадрат с данным индексом необходима для учета взаимосвязи и разброса коэффициентов. Определяется:
· Для этого составляется матрица дисперсионно ковариционную матрицу оценки коэффициентов (альфа-альфа). Внутри которой по диагонали сигмы от опр-х коэффициентов, а остально е- ковариации опр-х коэффициентов. Необходимо учитывать взаимосвязь и разброс коэффициентов. Дисперсия= Σ(х-хср.)2/n-1. Ковариация=Σ(х-хср.)*(у-уср.) /n-1.
· Общая формула: Сигма квадрат альфа итое = Оценка дисперсии эпсилы * [XT*X]-1
Где Оценка дисперсии эпсилы расчитывается как остаточная сумма квадратов/(число пар наблюдений – число параметров модели).
Таким образом: Н1: tр >tт – коэф значим. Н0: tр= tт; tр <tт.
2. Проверка модели на адекватность – на сколько хорошо модель описывает наши данные (явление).
Н0: α0 = α1 = …= αi = 0 – модель не адекватна.
Н1: α0 ≠ α1 ≠… ≠ α i ≠ 0.
Σ (уn – yср)2 = Σ(уn – ŷn)2 + Σ (ŷn – уср)2, где Σ (уn – yср)2 = TSS (общая сумма квадратов отклонений), Σ(уn – ŷn)2 = RSS (сумма квадратов остатков), Σ (ŷn – уср)2 = FSS (сумма квадратов отклонений за счет регрессии).уn – значение зависимой переменной, yср - среднее значение выборочных данных, ŷn - оцененное n-ное значение, рассчитанное по выбранной модели.
Чем меньше, RSS тем лучше модель.
Следовательно: TSS= RSS+ FSS – основное тождество дисперсионного анализа. Если RSS>FSS, то модель не значима.
Коэффициент детерминации: R2 = FSS/ RSS. В промежутке от 0 до 1 (либо в %). R2 – это та часть вариации признака, которая объясняется уравнением регрессии. Чем показатель выше, тем лучше (например, 60% - можно говорить об адекватности модели).
По модели можно прогнозировать, если коэффициенты значимы и модель адекватна. α1 при увелечении Х на еденицу У изменится на ±α1.
Предсказание значений так же можно осуществить, вспоминая мнк. Когда выведена модель регрессии для теоретического у (т.е. у с крышечкой). Подставляя х в модель, можно находить значение у. Таким образом предсказывая влияние одного фактора на другой.
Если расчёт корреляции характеризует силу связи между двумя переменными, то регрессионный анализ служит для определения вида этой связи и дает возможность для прогнозирования значения одной (зависимой) переменной отталкиваясь от значения другой (независимой) переменной.
· Чтобы вызвать регрессионный анализ в SPSS, выберите в меню Analyze... (Анализ) Regression... (Регрессия)
Откроется соответствующее подменю.
Разделы этой главы соответствуют опциям вспомогательного меню. Причём при изучении линейного регрессионного анализа снова будут проведено различие между простым анализом (одна независимая переменная) и множественным анализом (несколько независимых переменных). Собственно говоря, никаких принципиальных отличий между этими видами регрессии нет, однако простая линейная регрессия является простейшей и применяется чаще всех остальных видов.
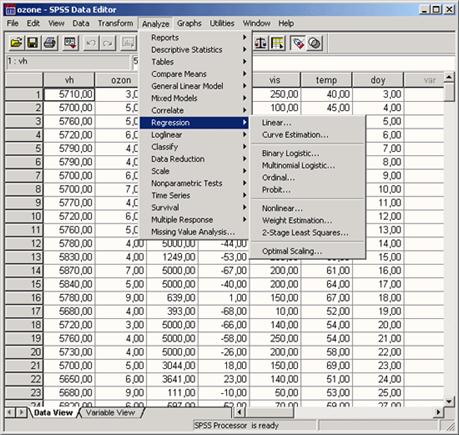
Рис. 16.1: Вспомогательное меню Regression (Регрессия)
Для проведения линейного регрессионного анализа зависимая переменная должна иметь интервальную (или порядковую) шкалу. В то же время, бинарная логистическая регрессия выявляет зависимость дихотомической переменной от некой другой переменной, относящейся к любой шкале. Те же условия применения справедливы и для пробит-анализа. Если зависимая переменная является категориальной, но имеет более двух категорий, то здесь подходящим методом будет мультиномиальная логистическая регрессия. Новшеством в 10 версии SPSS является порядковая регрессия, которую можно использовать, когда зависимые переменные относятся к порядковой шкале. И, наконец, можно анализировать и нелинейные связи между переменными, которые относятся к интервальной шкале. Для этого предназначен метод нелинейной регрессии.
Методы криволинейного приближения, весовые оценки и 2-ступенчатые наименьшие квадраты исследуют соответственно приближённость пути прохождения кривых при помощи компенсационных кривых, регрессионный анализ для изменяющейся дисперсии и проблемы из области эконометрии.
Переменные:
1. Предсказывающие переменные (предикаторы) или независимые переменные (факторы) – такие переменные, для которых обычно можно устанавливать желаемые значения (например, начальную температуру или скорость подачи катализатора), либо те, которые можно наблюдать, но не управлять ими (например, влажность воздуха).
2. Зависимые переменные или переменные-отклики.
В результате преднамеренных изменений или изменений, происшедших с независимыми переменными случайно, появляется эффект, который передается на другие переменные, на отклики (например, на окончательный цвет или чистоту хим продукта).
Разделение на предикаторы и отклики не всегда вполне четко и иногда зависит от наших целей. Однако роли переменных обычно легко различимы.
Общее описание модели регрессии:
Смысл РА (регрессионный анализ): РА устанавливает функциональные связи между зависимой переменной (У) и независимыми переменными (Хi), где i принадлежит (1;n), где
Х-входная переменная; регрессор.
У- регрессанд, функция отклика.
Х, У – количественные переменные.
Если i=1, то анализ однофакторный (парная регрессия)
Если i от 2 до n, то многофакторный (множественная регрессия).
1. Однофакторная модель регрессионного анализа: Y = α 0 + αiX + ξ
У – зависимая переменная (Пр.: выручка от реализации т,р,у).
Х – независимая переменная (Пр.: цена за 1 ед.)
Альфа – параметры модели (коэффициенты).
Эпсила – случайная составляющая, с мат ожиданием = 0 и сигмой квадрат (дисперсией) = константе. Подчинена нормальному закону распределения.
2. Многофакторная модель: Y = α 0 + α 1 X 1 + α 2 X 2 +... + αNXi + ξ, N= от 0, i от 1.
Х1,2, i – экзогенные переменные (вызванные внешними причинами).
Если эпсила постоянна, то явление называется гомоскедастичность. Если нет – гетеро.
Если присутствует взаимосвязь между Xi явлениями, то называется мультиколлиниарность.
Чем меньше факторов в модели – тем она более точная. Ошибка репрезентативности (эторазницамеждузначениемпоказателя, полученногоповыборке, игенеральнымпараметром) – имеем дело с выборкой, а результаты исследования переносим на ген совокупность, поэтому в модели присутствует епсила.
Выбор линии регрессии: МНК.
МНК используется для оценки параметров (коэффициентов а0 и а1) модели. Суть метода: оценить коэффициенты модели таком образом, чтоб сумма квадрата ошибок индивидуальных значений признака у от теоретич у с крышечкой – была минимальной.Цель - минимизировать квадраты отклонений линии регрессии от наблюдаемых точек.
По этим данным строим диаграмму рассеяния
1. 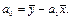
 Пример для однофакторного анализа:
Пример для однофакторного анализа:
S(yi – ŷ)2 = S(yi – a0 – a1xi)2 ® min
У с крышечкой – предсказанное значение (теоретическое).
На пример. У –выручка: 10; 5; 20. Х – цена: 5; 2; 1. Находим: уср. и хср.: 11,6 и 3 соответсвенно. Строим еще 4 столбца со значениями:
· у – уср.: -2;-7;8.
· х – хср.: 2;-1;-2.
· (х – хср.)*(у – уср.): -4;7;-16. Сумм= -13
· (х – хср.)2: 4;1;4. Сумм=9.
Далее по формуле: Y = α 0 + αiX + ξ, находим:
· Альфа1 = -13/ 9= -1,44.
· Альфа0 = 11,6 – (-1,44)*3 = 16,32
Выходит модель следующего вида: ŷ = 16,32 – 1,44*х.
Правильность расчёта параметров уравнения регрессии может быть проверена сравниванием сумм ∑у = ∑ŷ.
Оценка модели с помощью МНК: Далее строим по ней график прямой. Откладываем точки на оси «выручка», «цена». И какая точка будет наиболее приближена к графику, та вариация и несет наименьшую ошибку. Либо по формуле: у – ŷ = е (ошибка, остаток, находится для каждого у подставляя х).е стремится к минимуму.
2. Для линейной функции:
| x | ||||||
| y | 5,2 | 6,3 | 7,1 | 8,5 | 9,2 | 10,0 |
На опыте получены значения x и y, сведенные в таблицу. Найти прямую по методу наименьших квадратов.
Решение. Находим:
Σ xi=21, Σ yi=46,3, Σ xi2=91, Σxiyi=179,1.
91a+21b=179,1,
21a+6b=46,3, отсюда находим a=0,98 b=4,3.
3. А также матричным способом (например, для многофакторной модели), путем транспонирования матрицы. При учете того, что матрица содержит столько строк, сколько пар наблюдений. Содержит столбцов, сколько коэффициентов в модели (х1,х2,хн, у). Каждый столбец матрицы это, что находится при коэффициенте в модели.

Простая регрессия представляет собой регрессию между двумя переменными
—у и х, т.е. модель вида 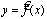
, где у — результативный признак; х - признак-фактор.
Множественная регрессия представляет собой регрессию результативного
признака с двумя и большим числом факторов, т. е. модель вида 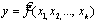





 2015-04-20
2015-04-20 3438
3438
