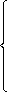Факторные нагрузки

Пр.: Теперь проведем анализ главных компонент и рассмотрим решение с двумя факторами. Для этого рассмотрим корреляции между переменными и двумя факторами (или "новыми" переменными), как они были выделены по умолчанию; эти корреляции называются факторными нагрузками.

STATISTICA ФАКТОРНЫЙ АНАЛИЗ	Факторные нагрузки (Нет вращения) Главные компоненты
Переменная	Фактор 1	Фактор 2
РАБОТА_1 РАБОТА_2 РАБОТА_3 ДОМ_1 ДОМ_2 ДОМ_3	.654384.715256.741688.634120.706267.707446	.564143.541444.508212 -.563123 -.572658 -.525602
Общая дисперсия Доля общей дисп.	2.891313.481885	1.791000.298500

Т.О.: По-видимому, первый фактор более коррелирует с переменными, чем второй. Это следовало ожидать, потому что, как было сказано выше, факторы выделяются последовательно и содержат все меньше и меньше общей дисперсии.

Экспертное оценивание — процедура получения оценки проблемы на основе мнения специалистов (экспертов) с целью последующего принятия решения (выбора).

Существует две группы экспертных оценок:

· Индивидуальные оценки основаны на использовании мнения отдельных экспертов, независимых друг от друга.

· Коллективные оценки основаны на использовании коллективного мнения экспертов.

Совместное мнение обладает большей точностью, чем индивидуальное мнение каждого из специалистов. Данный метод применяют для получения количественных оценок качественных характеристик и свойств. Например, оценка нескольких технических проектов по их степени соответствия заданному критерию, во время соревнования оценка судьями выступления фигуриста.

Формирование гипотез:

· Влияние количественных факторов на другие количественные. Пр.: Была проведена акция. Положительно ли повлияла акция? Х1 ср – до акции, Х2 ср – после.

Н0 – не повлияло: Х1ср=Х2 ср.; Х1ср<Х2 ср. Н1: Х1ср>Х2 ср.

· Влияние качественных на количественные (и наоборот).анализ влияния качественных факторов на количественные (Пр.: влияет ли качество – уровень обслуживания на посещаемость – обращение клиентов в банк).

Результат анализа – да/нет. Т.е. влияет качественный фактор или нет.

Проверяется нулевая гипотеза: Н0: сигма1 в квадрате=сигма2 в квадрате = сигма житое в квадрате = 0!!! Если применяется эта гипотеза, то качественный фактор НЕ оказывает влияние на количественный.

Н1: сигма1 в квадрате ≠сигма2 в квадрате ≠сигма житое в квадрате ≠ 0. Значит качественный фактор оказывает влияние на количественный.

Методы линейного программирования (транспортная задача, задача оптимального раскроя, задача оптимальной смеси и пр.) используются для решения многих оптимизационных аналитических задач, где функциональные зависимости исследуемых явлений и процессов детерминированы. Задача линейного программирования при проведении экономического анализа состоит в поиске экстремальных значений исследуемых параметров объекта, доставляющих максимум (минимум) критерию при ресурсных ограничениях. Оптимальное линейное программирование. Нахождение максимума или минимума целевой функции при заданных ограничениях. Необходимое условие использования оптимального подхода к планированию и управлению (принципа оптимальности) — гибкость, альтернативность производственно-хозяйственных ситуаций, в условиях которых приходится принимать планово-управленческие решения. Традиционные критерии оптимальности: «максимум прибыли», «минимум затрат», «максимум рентабельности» и др.

Модель любой задачи линейного программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать; ограничения в виде системы линейных уравнений или неравенств; требование неотрицательности переменных.

В общем виде модель записывается следующим образом:

 целевая функция:

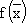= c1x1 + c2x2 +... + cnxn → max(min);

(2.1)

 ограничения:

a11x1 + a12x2 +... + a1nxn {≤ = ≥} b1, a21x1 + a22x2 +... + a2nxn {≤ = ≥} b2, ... am1x1 + am2x2 +... + amnxn {≤ = ≥} bm;

(2.2)

 требование неотрицательности:

xj ≥ 0,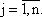

(2.3)

При этом a_ij, b_i, c_j (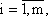 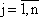) - заданные постоянные величины.

Задача состоит в нахождении оптимального значения функции (2.1) при соблюдении ограничений (2.2) и (2.3).

Систему ограничений (2.2) называют функциональными ограничениями задачи, а ограничения (2.3) - прямыми.

Вектор 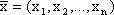, удовлетворяющий ограничениям (2.2) и (2.3), называется допустимым решением (планом) задачи линейного программирования. План 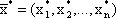, при котором функция (2.1) достигает своего максимального (минимального) значения, называется оптимальным.

Далее приведем примеры некоторых типовых задач, решаемых при помощи методов линейного программирования. Такие задачи имеют реальное экономическое содержание.

38. Кластерный анализ - совокупность математических методов, предназначенных для формирования относительно "отдаленных" друг от друга групп "близких" между собой объектов по информации о расстояниях или связях (мерах близости) между ними.

По смыслу аналогичен терминам: автоматическая классификация, таксономия, распознавание образов без учителя. Такое определение кластерного анализа дано в последнем издании "Статистического словаря".

Фактически "кластерный анализ" - это обобщенное название достаточно большого набора алгоритмов, используемых при создании классификации. В ряде изданий используются и такие синонимы кластерного анализа, как классификация и разбиение. Кластерный анализ широко используется в науке как средство типологического анализа. В любой научной деятельности классификация является одной из фундаментальных составляющих, без которой невозможны построение и проверка научных гипотез и теорий.

Большое достоинство кластерного анализа в том, что он позволяет производить разбиение объектов не по одному параметру, а по целому набору признаков. Кроме того, кластерный анализ в отличие от большинства математико-статистических методов не накладывает никаких ограничений на вид рассматриваемых объектов, и позволяет рассматривать множество исходных данных практически произвольной природы. Это имеет большое значение, например, для прогнозирования конъюнктуры, когда показатели имеют разнообразный вид, затрудняющий применение традиционных эконометрических подходов.

Кластерный анализ позволяет рассматривать достаточно большой объем информации и резко сокращать, сжимать большие массивы социально-экономической информации, делать их компактными и наглядными.

Важное значение кластерный анализ имеет применительно к совокупностям временных рядов, характеризующих экономическое развитие (например, общехозяйственной и товарной конъюнктуры). Здесь можно выделять периоды, когда значения соответствующих показателей были достаточно близкими, а также определять группы временных рядов, динамика которых наиболее схожа.

Кластерный анализ можно использовать циклически. В этом случае исследование производится до тех пор, пока не будут достигнуты необходимые результаты. При этом каждый цикл здесь может давать информацию, которая способна сильно изменить направленность и подходы дальнейшего применения кластерного анализа. Этот процесс можно представить системой с обратной связью.

Строение: пусть множество I = {I1, I2,…,In} обозначает n объектов (индивидов), принадлежащих некоторой популяции п1. Предположим также, что существует некоторое множество наблюдаемых показателей или характеристик С = (С1, С2, …, Ср)^Т, которыми обладает каждый индивид из I. Наблюдаемые характеристики могут быть как качественными так и количественными; однако основная часть нашего рассмотрения будет посвящена количественным данным, которое иногда называются измерениями. Результат измерения итой характеристики Ij объекта будет обозначаться символом Хij, а вектор Хj=[xij] размерности р×1 будет отвечать каждому ряду измерений (для житого индивида). Т.О., для множетсва индивидов I исследователь располагает множеством векторов измерений Х={Х1, Х2, …, Х n}, которые описывают множество I.Множество Х может быть представлено как n точек в р-мерном эвклидовом пространстве Ер.

Мера сходства: измерения могут быть представлены в виде матрицы. Неотрицательная вещественная функция s (Xi, Xj)=sij, называется мерой сходства, если:

1. 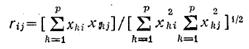0≤ s (Xi, Xj)<1 для Xi≠Xj

2. s (Xi, Xj)=1

3. s (Xi, Xj)= s (Xi, Xj)

Также пары значений мер сходства можно объединить в матрицу (где по диагонали 1). Sij – коэффициент меры сходства.

*Если каждый вектор измерения Х-итое состоит из 0 и 1, то это коэффициент ассоциации (парный коэф-т).

*коэфф-т корреляции – мера линейного сходства:

Пр.:

Расстояние: Неотрицательная вещественнозначная функция d (Xi, Xj) называется функцией расстояния (метрикой), если:

1. d (Xi, Xj)≥0 для всех Xi и Xj из Ер;

2. d (Xi, Xj)=0, тогда и только тогда, когда Xi = Xj;

3. d (Xi, Xj) = d (Xj, Xi);

4. d (Xi, Xj)≤ d (Xi, Xк)+ d (Xк, Xj), где Xi, Xj, Xк – любые три вектора из Ер.

Значение d (Xi, Xj) для заданных Xi и Xj называется расстоянием между Xi и Xj и эквивалентно расстоянию между Ii и Ij соответственно выбранным характеристикам С = (С1, С2, …, Ср)^Т. Некот функции расстояния(табл)

Однородность: неотъемлемой частью задачи кластерного анализа является понятие оптимального критерия (целевой функции), которое позволяет установить, когда достигается желательное разбиение. Для введения подобного критерия необходимо найти меру внутренней однородности кластера и меру разнородности кластеров между собой.

Пусть I = {I1, I2,…,In} и J={J1, J2,…, J_n2} обозначают два кластера объектов, принадлежащих некоторой популяции п. Пусть С = (С1, С2, …, Ср)^Тбудет множеством характеристик, которые генерируют два множества измерений Х={Х1, Х2, …, Х n₁} и Х={У1, У2, …, У n₂}, соответствующие I и J.

Обозначим через D={d(Xi, Yj), i=2,…,n1; j=1,2,…,n2} множество всех расстояний. Величину:

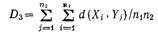D1(I,J)=min (либо макс) d (Xi, Yj), i=1,…,n1, j=1,…,n2 – будем называть минимальным (либо максимальным) локальным расстоянием между кластерами I и J, соответствующим данной функции расстояния d.

D3 – среднее расстояние между I и J, соответствующее данной функции расстояния d.

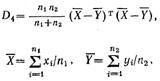- статистическое расстояние между кластерами I и J.

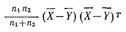- Матрица межгруппового рассеивания (к ней прибивляются внутригрупповые рассеивания I и J).

Сравнение кластерного и факторного анализов:

Главное сходство между кластерным и факторным анализами в том, что оба предназначены для перехода от исходной совокупности множества переменных (или объектов) к существенно меньшему числу факторов (кластеров).

Основные отличия

1. Цель факторного анализа – замена большого числа исходных переменных меньшим числом факторов. Кластерный анализ, как правило, применяется для уменьшения числа объектов путем их группировки. В кластерном анализе обычно переменные не группируются, а выступают в качестве критериев для группировки объектов. Кластерный анализ применяется обычно для выделения групп объектов, исходя из их сходства по измеренным признакам.

Группы объектов, выделенные в результате кластерного анализа на основе заданной меры сходства между объектами, называются кластерами.

2. Начиная с версии SPSS 10.0, программа позволяет проводить кластерный анализ и только объектов, и переменных. В последнем случае кластерный анализ может выступать как более простой аналог факторного анализа.

3. Различие в выполнении статистических операций:

§ факторный анализ – на каждом этапе извлечения фактора для каждой переменной подсчитывается доля дисперсии, которая обусловлена влиянием данного фактора.

§ кластерный анализ – вычисляется расстояние между текущим объектом и всеми остальными объектами, и кластер образует та пара, для которой расстояние оказалось наименьшим. Подобным образом каждый объект группируется либо с другим объектом, либо включается в состав существующего кластера. Процесс кластеризации конечен и продолжается до тех пор, пока все объекты не будут объединены в один кластер.

4. Вид кластерного анализа – иерархический кластерный анализ, часто используется в биологии, экономике, социологии, политологии, а в психологии, обычно анализируют переменные для определения статистических связей между ними; которые, как правило, указывают на сходство между теми или иными исследуемыми факторами.

5. Как и в случае факторного анализа, выполнение кластерного анализа и его результаты зависят от ряда параметров: способа вычисления расстояния между объектами, кластеризации индивидуальных объектов и т. д.

При проведении кластерного анализа отдельные кластеры могут формироваться при помощи пошагового слияния, для которого существует ряд различных методов. Важную роль играют иерархические и партиционные методы, причём последние применяются в подавляющем большинстве случаев. Оба эти метода можно задействовать, если пройти через меню Analyze (Анализ) Classify (Классифицировать). Они помещены в этом меню под именами Hierarchical Cluster... (Иерархический кластер) и K-Means Cluster... (Кластерный анализ методом к-средних).

АЛГОРИТМ ПОСЛЕДОВАТЕЛЬНОЙ КЛАСТЕРИЗАЦИИ (из книги Дюрана – «кластерный анализ»):

Рассмотрим I = {I1, I2,…,In} как множество кластеров {I1}, {I2}, …, {In}; выберем два из них, скажем Ii и Ij, которые в некотором смысле наиболее близки друг другу, и объединим их в один кластер. Новое множество кластеров, состоящее уже из n-1 кластеров, будет: {I1}, {I2}, …,{IiIj}, …, {In}.

Повторяя процесс мы получим последовательные множества кластеров, состоящие из n-2, n-3 и т.д. кластеров. В конце этой процедуры получится кластер, состоящий из n объектов и совпадающий с первоначальным множеством I = {I1, I2,…,In}.

В качестве меры расстояния примем квадрат евклидовой метрики d²ij. Для наглядности вычислим матрицу D={d²ij}, где d²ij – расстояния между Ii и Ij.

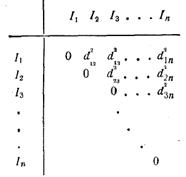
Предположим, что расстояние между Ii и Ij минимально, т.е., что d²ij = min{d²ij, i≠j}, образуем с помощью Ii и Ij новый кластер {Ii, Ij}. Построим новую (n-1)×(n-1) матрицу расстояния. Значения d²ij после первого объединения:

Легко видеть, что n-2 строки для этой матрицы можно непосредственно взять из старой, однако первую строку необходимо вычислить заново. Очевидно, вычисления будут сведены к минимуму, если удастся выразить d²ijк, к=1,2,…, n, к≠i≠j через элементы первоначальной матрицы.

Ланс и Уильямс предложили рекурсивную процедуру, в которой вычисления матрицы расстояний опираются только на значения расстояний в предыдущей матрице. Их рекурсивная сх предполагает использование мин (объединение 2х кластеров, имеющих наименьшее мин локальное расстояние) и макс локальных расстояний (билет 38), медианы, групповых средних и центра. Медианный метод такой же как центроидный, за исключением того, что здесь при объединении кластеров I и J предполагается, что ni=nj, и поэтому центр нового кластера лежит точно посередине между центрами старых клатеров. Уишарт считает, что процедуру Уорда можно объединить с пятью, рассмотренными выше.

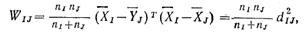Объединение кластеров I и J ведет к увеличению ВСК (внутригрупповая сумма квадратов) на величину Wij:

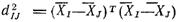Где

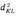Если кластер IUJ = L объединяется с К, то можно показать, что

Тогда: 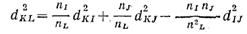, из этого следует, что: 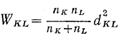, при подставке получаем: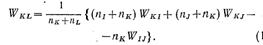

Последнее уравнение определяет вел ВСК при объединении К и IUJ.

Начиная с матрицы квадратов евклидовых расстояний (самой первой) D={d²ij, i=1,2,…,n; j=1,2,…,n} процедура заключается в объединении таких кластеров Ip и Iq, для которых d²pq=2Wpq минимально. Кластер Ip, состоящий из одного объекта, заменяется на IpUJq, а расстояния d²ip, i=1,2,…,n; j=1,2,…,n; i≠р, q в матрице D заменяются на d²ip=2Wip. Элементы q-го столбца и строки полагаются равными нулю, т.е.Sq становится «недействительным». Соответственно n_р заменяется на n_р + n_q, а n_р приравнивается к нулю. Равенство: d²ip=2Wip выполняется для всех {d²ij}, i, j≠q. Подставляем:

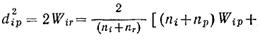
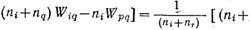
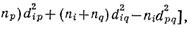где n_r=n_p+n_q. Если на каждом шаге объединения р-е столбцы и строки матрицы D преобразовываются по последней формуле, то равенство d²ij будет выполнятся для всех d²ij и всех действительных множеств Si и Sj. Заметим, что d²ij в его формуле не является евклидовым расстоянием, если не рассматриваются только два кластера, содержащих по одному элементу.

Окончательная запись алгоритма группировки:

1) Найдем d²pq=min{ d²ij}, i=1,…, j-1; j=2,…,n; ni> 0; nj>0;

2) Увеличение целевой функции при объединении двух кластеров IpIq равно Wpq=1/2 d²pq;

3) Ip заменяется на SpUSq; строка { d²iр} и столбец { d²рj}матрицы D пересчитывается по последней формуле, i=1,2,…,р-1; ni> 0; j=р+1,…, n; j≠q; nj> 0;

4) Полагаем n_р= n_р+ n_q и n_q=0, превращая Sq в недействительное множество;

5) Записываем элементы кластера Sq в кластер Sр, возвразаемся к (1) и повторяем процедуру n-2 раз.

Пр.: Этапы кластерного анализа