Статистические оценки параметров распределения. Обычно в распоряжении исследователя имеются лишь выборочные данные. Если из теоретических соображений удалось установить, какое именно распределение имеет признак генеральной совокупности, то возникает задача оценки параметров, которыми определяется это распределение. Для описания случайных величин используются описательные статистики: минимум, максимум, среднее, дисперсия, стандартное отклонение, медиана, мода и т.д. Статистики дают общее представление о значениях, которые принимают случайные величины. Получаемые оценки могут носить точечный и интервальный характер.
Оценка называется точечной, если определяется одним числом; интервальной – если по данным выборки строится числовой интервал, внутри которого на основании заранее выбранной вероятности находится оцениваемый параметр.
Оценка должна быть близка к оцениваемому параметру. Близость характеризуется несмещенностью оценки, ее состоятельностью и эффективностью.
Несмещенность оценки означает отсутствие систематических погрешностей в наблюдаемых данных, для этого ее математическое ожидание должно быть равно оцениваемому параметру.
Состоятельность оценки заключается в том, что с ростом числа наблюдений дисперсия стремится к нулю.
Для исследуемого параметра оценка эффективна, если имеет минимальную дисперсию среди всех возможных оценок, построенных по данной выборке.
Пусть из генеральной совокупности извлечена выборка объема n. Выборочное среднее (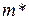 ) – сумма значений переменной, делённая на n (число значений переменной)
) – сумма значений переменной, делённая на n (число значений переменной)
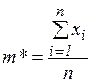 .
.
Выборочное среднее может быть посчитано по частотно-вариационному ряду
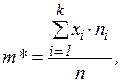
где k – количество вариантов в ряду, или по интервальному ряду
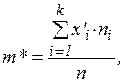
где 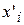 - середина i -го интервала, k - количество интервалов.
- середина i -го интервала, k - количество интервалов.
Среднее выборочное является несмещенной, состоятельной и эффективной оценкой математического ожидания генеральной совокупности, т.е. точечная оценка математического ожидания является доброкачественной
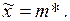
Выборочная дисперсия (D*)- мера изменчивости случайной величины. Вычисляется по формуле:
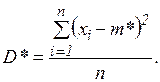
Значение 0 означает отсутствие изменчивости, т.е. переменная постоянна. Выборочная дисперсия является смещенной оценкой дисперсии генеральной совокупности, поэтому доброкачественной оценкой генеральной дисперсии является исправленная выборочная дисперсия
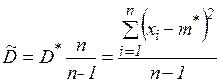 .
.
Выборочное стандартное отклонение (S) - корень квадратный из дисперсии. Более удобная характеристика, так как измерена в тех же единицах, что и исходная величина. Чем выше дисперсия и стандартное отклонение, тем сильнее разбросаны значения случайной величины относительно среднего. Для оценки среднего квадратичного отклонения генеральной совокупности применяют выборочное среднее квадратичное отклонение
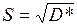
или исправленное среднее квадратичное отклонение
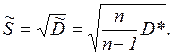
Для более подробного описания свойств распределения вводятся эмпирические начальные
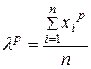
и центральные
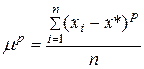
моменты p -го порядка или их комбинаций. В частности, коэффициент асимметрии позволяет судить о симметричности выборочных данных
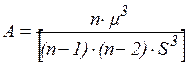
Если коэффициент значительно отличается от 0, распределение является асимметричным. Показатель эксцесса служит мерой крутизны (заостренности) гистограммы по отношению к кривой нормального распределения (для нормально распределенной случайной величины Е=0).
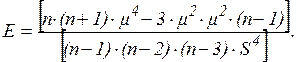
Медиана – значение, которое разбивает выборку на две равные части. Половина наблюдений лежит выше медианы, и половина – ниже. В некоторых случаях, например, при описании доходов населения медиана более удобна, чем среднее.
Медиана дает общее представление о том, где сосредоточены значения переменной, иными словами, где находится ее центр. Сумма абсолютных расстояний между точками выборки и медианой минимальна. Медиана вычисляется следующим образом. Выборка упорядочивается в порядке возрастания. Если количество элементов в выборке определяется как 2m+1 (нечетно), то медиана выборки оценивается как 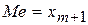 . Если число наблюдений четно, то медиана оценивается как
. Если число наблюдений четно, то медиана оценивается как 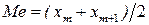 .
.
Квантиль – число tp, ниже которого находится p -я часть (доля) выборки.
Процентиль – значение квантили в процентах.
Мода – наиболее часто встречающееся выборочное значение, варианта, имеющая наибольшую частоту.
Доверительным интервалом для параметра 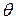 называется интервал
называется интервал 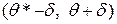 , который с заданной надежностью
, который с заданной надежностью 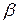 покрывает реальное значение параметра
покрывает реальное значение параметра 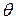 , здесь
, здесь 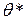 – оценка параметра,
– оценка параметра, 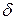 – точность оценки. Число
– точность оценки. Число 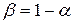 называется доверительной вероятностью, а значение
называется доверительной вероятностью, а значение 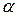 - уровнем значимости. В качестве
- уровнем значимости. В качестве 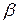 , как правило, выбираются значения, близкие к единице: 0,95; 0,99; 0,999.
, как правило, выбираются значения, близкие к единице: 0,95; 0,99; 0,999.
Точечная оценка 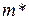 даже, если она несмещенная, состоятельная, эффективная дает приближенное значение параметра генеральной совокупности и, особенно для выборок малого объема, отличается от истинного значения параметра, т.е. от
даже, если она несмещенная, состоятельная, эффективная дает приближенное значение параметра генеральной совокупности и, особенно для выборок малого объема, отличается от истинного значения параметра, т.е. от 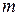 .
.
Представление о том, к каким ошибкам может привести замена параметра 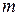 на его точечную оценку
на его точечную оценку 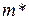 и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы дает мера достоверности (или интервальная оценка).
и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы дает мера достоверности (или интервальная оценка).
В качестве меры достоверности принимают:
1) доверительную вероятность 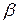 (точный метод), с которой истинное значение параметра а будет находится в заданном относительно стат. оценки интервале;
(точный метод), с которой истинное значение параметра а будет находится в заданном относительно стат. оценки интервале;
2) доверительный интервал 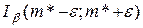 (грубый метод) относительно статистической оценки, в который с заданной вероятностью
(грубый метод) относительно статистической оценки, в который с заданной вероятностью 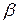 попадет истинное значение параметра
попадет истинное значение параметра 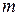 .
.
Понятие оценки меры достоверности. Назначим некоторую достаточно большую вероятность (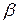 = 0,9; 0,95; 0,997) такую, что событие с этой вероятностью
= 0,9; 0,95; 0,997) такую, что событие с этой вероятностью 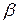 можно считать практически достоверным.
можно считать практически достоверным.
Требуется найти доверительный интервал: 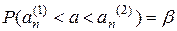 ,
,
где границы интервала 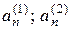 – доверительные границы.
– доверительные границы.
Интервальная оценка параметра 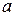 (доверительный интервал) - числовой интервал
(доверительный интервал) - числовой интервал 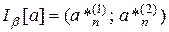 относительно статистической оценки параметра, который с заданной вероятностью
относительно статистической оценки параметра, который с заданной вероятностью 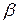 накрывает реальное значение параметра
накрывает реальное значение параметра 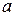 .
.
Чаще всего доверительный интервал выбирают симметричным относительно статистического параметра (см. рис. 2.1).
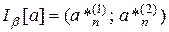 ,
, 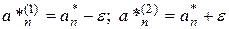 .
.
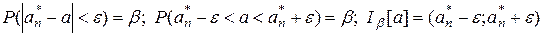 .
.
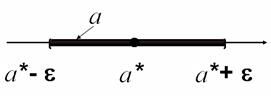
Рисунок 2.1 - Симметричный доверительный интервал
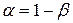 - уровень значимости, вероятность того, что расхождения между параметром и его оценкой больше либо равно абсолютной величине доверительного интервала:
- уровень значимости, вероятность того, что расхождения между параметром и его оценкой больше либо равно абсолютной величине доверительного интервала:
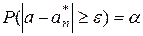 .
.
Чаще всего 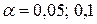 .
.
Доверительный интервал – числовой интервал значений параметра 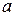 ГС, которые не противоречат опытным данным или совместимы с опытными данными. Границы интервала и его величина получены по выборочным данным и поэтому случайны в отличие от самого параметра
ГС, которые не противоречат опытным данным или совместимы с опытными данными. Границы интервала и его величина получены по выборочным данным и поэтому случайны в отличие от самого параметра 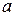 .
.
Величина доверительного интервала 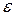 существенно зависит:
существенно зависит:
- от объема выборки (с ростом 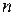 величина интервала уменьшается;
величина интервала уменьшается;
- от величины доверительной вероятности: чем больше доверительная вероятность 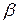 , тем больше
, тем больше 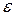 .
.
Оценка доверительного интервала для математического ожидания. Пусть для параметра 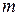 генеральной совокупности получена доброкачественная оценка
генеральной совокупности получена доброкачественная оценка 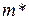 . Нужно оценить полученную при этом ошибку «грубым» и «точным» методами. Определение
. Нужно оценить полученную при этом ошибку «грубым» и «точным» методами. Определение 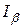 возможно, если известен закон распределения статистической оценки, который зависит от закона распределения самой СВ, и от конкретного значения параметра ГС.
возможно, если известен закон распределения статистической оценки, который зависит от закона распределения самой СВ, и от конкретного значения параметра ГС.
«Грубый метод» используется при следующих допущениях:
- допущение нормальности закона распределения СВ;
- замена параметров этого закона их статистическими оценками.
Пусть имеется случайная величина 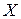 – описывающая ГС, с неизвестными параметрами
– описывающая ГС, с неизвестными параметрами 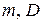 . Найти доверительный интервал для
. Найти доверительный интервал для 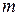 , если задана доверительная вероятность и получены результаты эксперимента. Т.е., дано:
, если задана доверительная вероятность и получены результаты эксперимента. Т.е., дано: 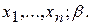 Найти:
Найти: 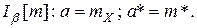
Известно, что статистическая оценка математического ожидания равна:
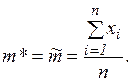
В качестве оценки реального 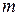 по выборке принимается среднее арифметическое
по выборке принимается среднее арифметическое 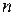 независимых наблюденных значений.
независимых наблюденных значений.
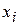 – некоторый экземпляр случайной величины
– некоторый экземпляр случайной величины 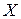 с параметрами
с параметрами 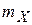 . Оценка
. Оценка 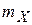 - это сумма
- это сумма 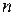 независимых одинаково распределенных СВ, тогда, по центральной предельной теореме при достаточно большом
независимых одинаково распределенных СВ, тогда, по центральной предельной теореме при достаточно большом 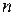 закон распределения этой суммы близок к нормальному.
закон распределения этой суммы близок к нормальному.
В практической статистике даже при относительно небольшом числе испытаний (от 10 до 20) считается, что закон распределения стремится к нормальному. Тогда, вероятность попадания в интервал для нормального закона равна:
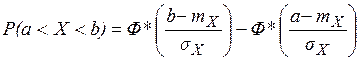 ,
,
В симметричный интервал 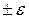 относительно
относительно 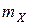 :
:
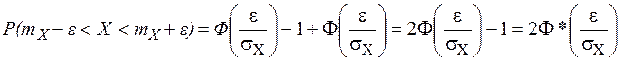 .
.
Рассматриваемая СВ 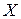 - это оценка матожидания:
- это оценка матожидания: 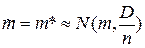 ,
,
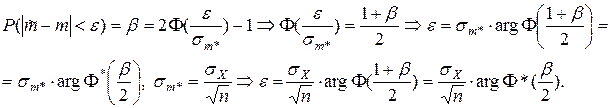

Величина доверительного интервала для матожидания равна (“грубый метод”):
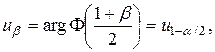
где 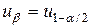 - квантиль нормального распределения. Тогда
- квантиль нормального распределения. Тогда
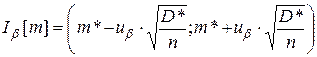 .
.
Для примера 1 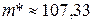 ,
, 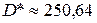 ,
, 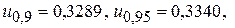
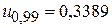 . Тогда
. Тогда 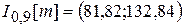 ,
, 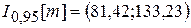 ,
, 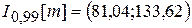 .
.
Полученные с помощью «грубого» метода границы интервалов для математического ожидания, нанесем на полигон частот (см. рис. 2.2).
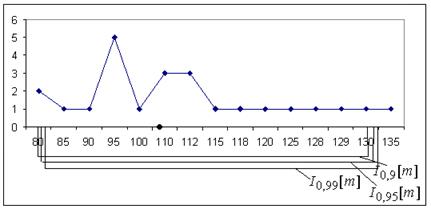
Рисунок 2.2 - Границы доверительных интервалов для мат. ожидания
“Точный ” метод оценки достоверности матожидания. Если 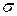 не известно, то используют
не известно, то используют 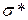 и вместо нормального распределения
и вместо нормального распределения 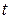 -распределение Стьюдента:
-распределение Стьюдента:
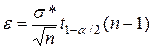 ,
,
где 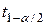 - квантиль
- квантиль 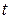 -распределения (табличное значение).
-распределения (табличное значение).
Доверительный интервал для 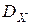 . Дана СВ
. Дана СВ 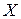 с нормальным законом распределения и неизвестными параметрами
с нормальным законом распределения и неизвестными параметрами 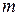 и
и 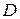 .Произведено
.Произведено 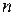 независимых испытаний. Требуется по заданной доверительной вероятности найти доверительный интервал для
независимых испытаний. Требуется по заданной доверительной вероятности найти доверительный интервал для 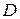 .
.
В качестве оценки 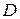 принимаем:
принимаем:
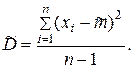
По аналогии с математическим ожиданием, оценка 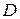 грубым методом:
грубым методом:
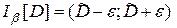 ,
, 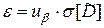 ,
, 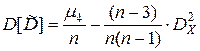
Чтобы воспользоваться этими формулами вместо реальных 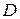 и
и 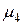 пользуются их оценками:
пользуются их оценками:
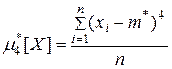
Нормальный закон:
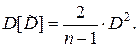
Равномерный:
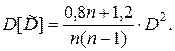
Оценка 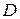 «точным» методом: если
«точным» методом: если 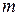 известно, то
известно, то
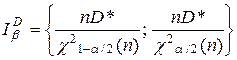 ;
;
если 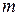 неизвестно, то берут
неизвестно, то берут 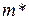 :
:
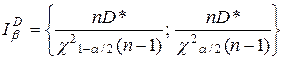 .
.
Контрольные вопросы
1. В чем разница между точечной и интервальной оценками?
2. Дайте определение медианы, моды, квантиля и процентиля.
3. Что такое мера достоверности и доверительный интервал?
4. Что такое мат. ожидание и дисперсия?
5. Чем «точный» метод оценки отличается от «грубого» метода?
 2015-04-30
2015-04-30 2348
2348
