Представление любой величины не в именованных, а относительных единицах существенно упрощает теоретические выкладки и придает результатам расчета большую наглядность. Под относительным значением какой-либо величины следует понимать ее отношение к другой одноименной величине, принятой за базисную:
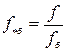 .
.
Следовательно, перед тем как представить какие-либо величины в относительных единицах, надо выбрать базисные единицы.
За базисный ток и базисное линейное напряжение примем некоторые произвольные величины Iб, Uб. Тогда базисная мощность трехфазной цепи будет определяться формулой
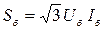 ,а базисное сопротивление:
,а базисное сопротивление: 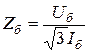 .
.
Отсюда вытекает, что только две базисные величины могут быть выбраны произвольно, а остальные являются связанными. Обычно выбирается 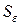 и Uб. Причем выбранные базисные величины должны быть едиными для всей расчетной схемы и применяться как к полным величинам, так и к их отдельным составляющим.Следовательно, параметры электрической системы в относительных единицах при выбранных базисных условиях будут вычисляться по формулам:
и Uб. Причем выбранные базисные величины должны быть едиными для всей расчетной схемы и применяться как к полным величинам, так и к их отдельным составляющим.Следовательно, параметры электрической системы в относительных единицах при выбранных базисных условиях будут вычисляться по формулам:
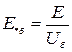 ;
; 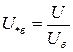 ;
; 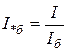 ;
; 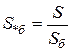 ;
; 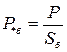 ;
; 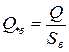 ;
;
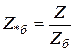
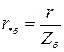
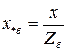 .
.
Здесь U, I, S, Z - параметры в именованных единицах. При задании паспортных данных оборудования в относительных единицах их параметры относят к номинальным параметрам элементов:
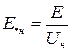 ;
; 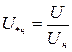 ;
; 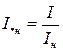 ;
; 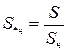 ;
; 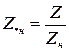 .
.
Относительное сопротивление при номинальных условиях показывает относительное падение напряжения на элементе при протекании номинального тока, что придает физическую наглядность параметру:
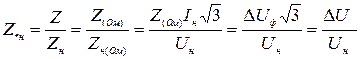 =
= 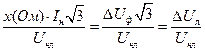 .
.
При расчетах в системе относительных единиц исходные параметры обычно задаются либо в именованных единицах (и.е), либо в относительных единицах (о.е.) при номинальных условиях элемента. При построении расчетных схем замещения требуется их перевод в относительные единицы при базисных условиях с обязательным приведением параметров на основную ступень.
При этом для построения расчетных формул требуется решение двух задач:
1) Заданы параметры в и.е. - требуется их перевод в о.е. при базисных условиях с приведением на основную ступень.
2) Заданы параметры в о.е. при номинальных условиях - требуется их перевод в о.е. при базисных условиях с приведением на основную ступень.
Рассмотрим расчетные формулы на примере сопротивлений и э.д.с..
1) Заданы 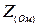 ,
, 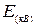 .
.
. При приближенном приведении и при обычно используемом условии 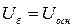 формулы принимают вид:
формулы принимают вид:
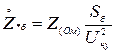 ;
; 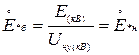 .
.
где 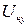 - номинальное напряжение ступени, где установлен элемент.
- номинальное напряжение ступени, где установлен элемент.
2) Заданы 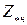 ,
, 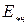 .
. 
При приближенном приведении и при обычно используемых условиях 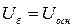 и
и 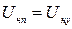 формулы имеют вид:
формулы имеют вид:
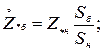
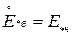 .
.
 2015-05-05
2015-05-05 876
876








