Найдём полумарковскую матрицу для цепи Маркова с непрерывным временем, заданной матрицей Q инфинитезимальных характеристик qk n.
Запишем преобразование Фурье-Стилтьеса по x от элементов Ak n(x) полумарковской матрицы
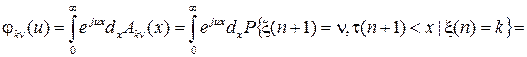
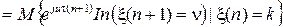 ,
,
здесь In (A) – индикатор события A.
Для цепи Маркова k (t) с непрерывным временем рассмотрим при k ¹n следующее условное математическое ожидание
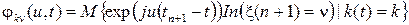 ,
,
где tn<t<tn+ 1, а tn – последовательность моментов изменения состояний цепи Маркова k (t).
При k =n очевидно, что jnn(u,t)=0.
Для функций j k n(u,t) по формуле полной вероятности, аналогично выводу обратной системы дифференциальных уравнений Колмогорова, можно записать следующие равенства
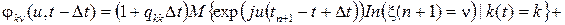
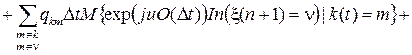
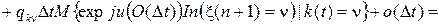
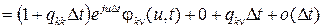 .
.
В силу однородности цепи Маркова k (t) функции j k n(u,t)= j k n(u) – не зависят от момента времени t, поэтому составленное равенство можно переписать в виде
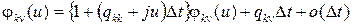 ,
,
из которого получим
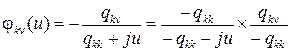 ,
,
здесь первый сомножитель является характеристической функцией экспоненциально распределнной случайной величины с параметром (– qkk), а второй сомножитель определяет распределение вероятностей, так как
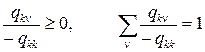 .
.
В определении функции j k n(u) для цепи Маркова рассматривается величина tn +1 –t, имеющая смысл остаточного времени пребывания цепи в заданном состоянии. В силу того, что эта величина имеет экспоненциальное распределение, полная продолжительность пребывания в этом состоянии также распределена экспоненциально с тем же параметром, что и остаточная продолжительность, поэтому для элементов полумарковской матрицы, определяющей цепь Маркова с непрерывным временем, можно записать следующее равенство
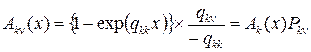 ,
,
из которого следует, что цепь Маркова является процессом марковского восстановления, определяемого набором экспоненциальных функций распределения
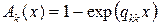
и стохастической матрицей P вероятностей
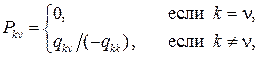
переходов вложенной цепи Маркова за один шаг.
Такой способ задания цепей Маркова с непрерывным временем в виде процесса марковского восстановления широко применяется при имитационном моделировании этих цепей.
6.3. Исследование процесса марковского восстановления методом дополнительной переменной z (t)
Рассмотрим процесс марковского восстановления k (t), заданный стохастической матрицей P и набором функций распределения Ak (x).
Для нахождения стационарного распределения вероятностей
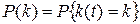 (9)
(9)
определим случайный процесс z (t) как длину интервала от момента t до момента очередного отказа (замены элемента).
Очевидно, двумерный случайный процесс { k (t), z (t)} марковский, поэтому для его распределения вероятностей
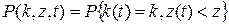
можно записать следующие равенства
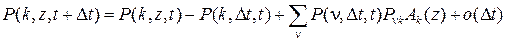 ,
,
из которых нетрудно получить систему дифференциальных уравнений Колмогорова
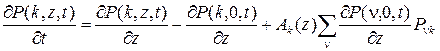
и для стационарного распределения P (k,z,t)º P (k,z) переписать в виде
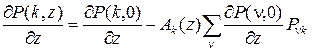 .
.
Интегрируя левую и правую части этого равенства, получим
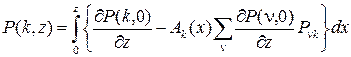 .
.
В силу условия согласованности вероятностных распределений, одномерное маргинальное распределение P (k) запишем следующим образом
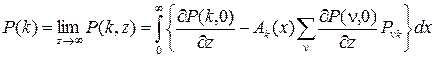 . (10)
. (10)
В силу необходимого условия сходимости несобственного интеграла, можно записать следующее равенство
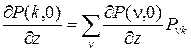 ,
,
которое совпадает с системой уравнений Колмогорова
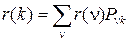

для стационарного распределения вероятностей r (k) состояний вложенной цепи Маркова x(n), поэтому
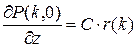 . (11)
. (11)
Мультипликативную постоянную C найдём из условия нормировки следующим образом.
Применяя равенство (11), перепишем (10)
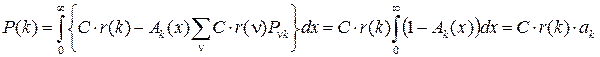 ,
,
где ak – среднее значение срока службы элемента вида k.
Таким образом
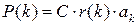 ,
,
а в силу условия нормировки запишем
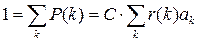 ,
,
откуда получим
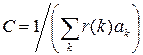 ,
,
следовательно, стационарное распределение вероятностей P (k) значений процесса марковского восстановления k (t) имеет вид
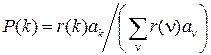 . (12)
. (12)
Рассмотрим применение формулы (12) для нахождения стационарного распределения вероятностей значений цепи Маркова с непрерывным временем, заданной матрицей Q инфинитезимальных характеристик, для которой выше было показано, что она является процессом марковского восстановления с матрицей вероятностей переходов вида
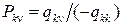 (13)
(13)
и экспоненциальными функциями распределения времени пребывания процесса в каждом состоянии.
Известно, что распределение вероятностей значений вложенной цепи Маркова определяется системой
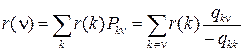 , (14)
, (14)
которую можно переписать в виде
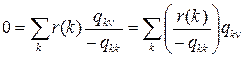 .
.
Так как эта система совпадает с системой уравнений Колмогорова для стационарных вероятностей P (k) значений цепи Маркова с непрерывным временем, то
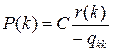 , (15)
, (15)
а в силу условия нормировки и равенства
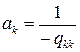
для цепей Маркова, равенство (15) имеет вид
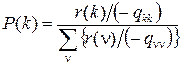 (16)
(16)
и совпадает с (12). Здесь распределение r (k) определяется системой (14) и условием нормировки.
6.4. Исследования полумарковского процесса методом дополнительной переменной y (t)
Для исследования полумарковского процесса k (t), определяемого полумарковской матрицей A (x), применение случайного процесса z (t) требует введения ещё одной дополнительной переменной, поэтому рассмотрим случайный процесс y (t), равный длине интервала от момента последнего отказа (замены элемента) до текущего момента времени t. В этом случае двумерный процесс { k (t), y (t)} является марковским процессом.
Обозначим
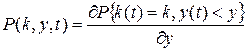 , (17)
, (17)
тогда для этого распределения вероятностей можно при tn<t<tn +1= tn +t(n+ 1) записать следующее равенство
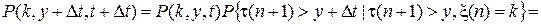
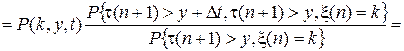
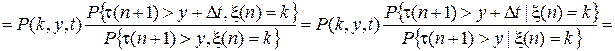
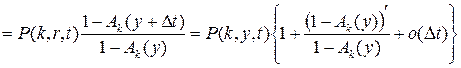 ,
,
из которого получим уравнение
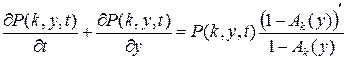 .
.
Для стационарного распределения
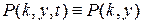
это уравнение перепишем в виде
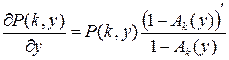 . (18)
. (18)
Для нахождения частного решения этого уравнения необходимо записать краевое по y условие для решения P (k,y) уравнения (18). Такое краевое условие получим следующим образом. При tn<t<tn +1= tn +t(n+ 1) в силу (17) можно записать
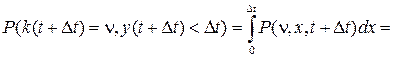
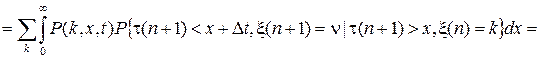
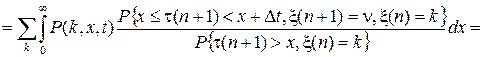
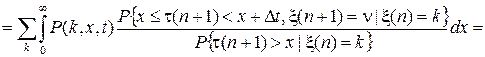
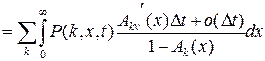 .
.
Поделив левую и правую части этого равенства на D t и полагая, что D t сходится к нулю, получим равенство
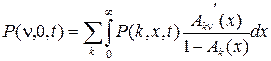 ,
,
которое в стационарном режиме имеет вид
 (19)
(19)
и определяет краевое условие при y =0 для решения P (k,y) уравнения (18).
Общее решение уравнения (18) можно записать в виде
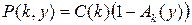 . (20)
. (20)
Для определения постоянных C (k), воспользуемся краевым условием (19), подставив в которое (20), получим равенство
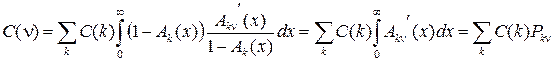 ,
,
которое совпадает с системой уравнений Колмогорова для стационарного распределения вероятностей r (k) значений вложенной цепи Маркова, поэтому
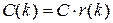 ,
,
и в силу (20) запишем
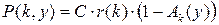 .
.
В силу определения (17) функций P (k,y) и условия согласованности распределений одномерное маргинальное распределение P (k) имеет вид
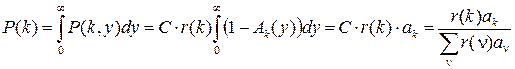 . (21)
. (21)
Отметим, что распределение (21) для полумарковского процесса совпадает с распределением вероятностей (12) для процесса марковского восстановления.
6.5. Исследование полумарковского процесса методом дополнительных переменных z (t) и s (t)
Стационарное распределение вероятностей для значений полумарковского процесса, определяемого полумарковской матрицей A (x), можно найти и другим способом, применяя процессы z (t) и s (t), где процесс z (t) определён выше, а процесс s (t) для tn<t<tn+ 1 определим равенством
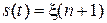 ,
,
то есть процесс s (t) на интервале tn<t<tn+ 1 принимает и сохраняет то значение вложенной цепи Маркова, которое она принимает в конце рассматриваемого интервала времени. Напомним, что процесс k (t) на этом интервале принимает и сохраняет то значение, которое вложенная цепь принимает в начале рассматриваемого интервала времени.
Построенный трёхмерный случайный процесс { k (t), z (t), s (t)} является марковским, поэтому для его распределения вероятностей
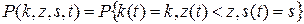
можно записать равенства
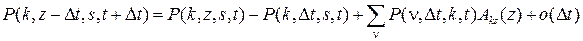 ,
,
из которых нетрудно получить систему дифференциальных уравнений Колмогорова
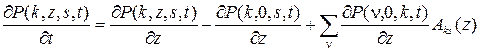 .
.
Для стационарного распределения вероятностей эту систему перепишем в виде
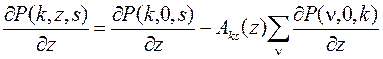 .
.
Интегрируя по z левую и правую части этого равенства, получим
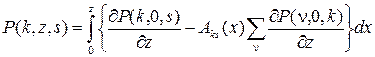 .
.
В силу условия согласованности вероятностных распределений, двумерное маргинальное распределение P (k,s) запишем следующим образом
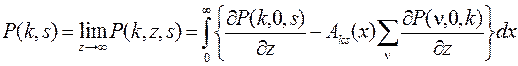 . (22)
. (22)
А в силу необходимого условия сходимости несобственного интеграла можно записать следующее равенство
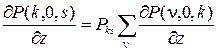 , (23)
, (23)
подставив которое в (22), получим
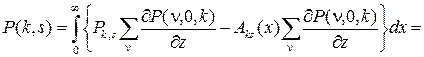
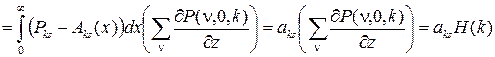 , (24)
, (24)
здесь
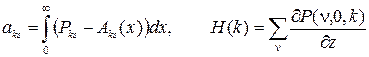 .
.
Для нахождения величин H (k) просуммируем по k равенства (23), получим систему уравнений относительно H (k)
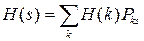 ,
,
совпадающую с системой уравнений Колмогорова для стационарного распределения вероятностей r (k) состояний вложенной цепи Маркова x(n), поэтому
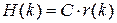 .
.
Подставляя найденное выражение в (24), запишем
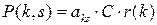 .
.
Так как в силу (4)
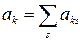 ,
,
то
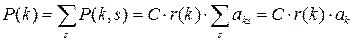 ,
,
следовательно, для стационарного распределения вероятностей P (k) значений полумарковского процесса k (t) можно записать равенство
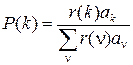 ,
,
совпадающее с полученным ранее, методом дополнительной переменной y (t), равенством (21).
 2015-05-05
2015-05-05 1151
1151