Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
Функция называется целевой функцией (или линейной формой) задачи.
Ограничение-неравенство исходной задачи линейного программирования, имеющее вид “ 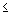 ”, можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида “
”, можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида “ 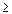 ” – в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство
” – в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство
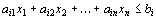
В то же время каждое уравнение системы ограничений
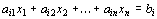
можно записать в виде неравенств:
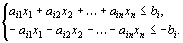
Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.
Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса.
Отметим, наконец, что если переменная 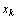 , не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными
, не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными 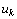 и
и 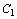 , приняв
, приняв 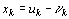 .
.
Пример 1. Записать в форме основной задачи линейного программирования следующую задачу: найти максимум функции 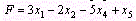 при условиях
при условиях
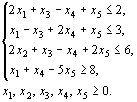
Решение. В данной задаче требуется найти максимум функции, а система ограничений содержит четыре неравенства. Следовательно, чтобы записать ее в форме основной задачи, нужно перейти от ограничений-неравенств к ограничениям-равенствам. Так как число неравенств, входящих в систему ограничений задачи, равно четырем, то этот переход может быть осуществлен введением четырех дополнительных неотрицательных переменных. При этом к левым частям каждого из неравенств вида“ 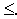 “ соответствующая дополнительная переменная прибавляется, а из левых частей каждого из неравенств вида “
“ соответствующая дополнительная переменная прибавляется, а из левых частей каждого из неравенств вида “ 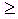 ” вычитается. В результате ограничения принимают вид уравнений:
” вычитается. В результате ограничения принимают вид уравнений:
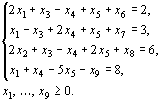
Следовательно, данная задача может быть записана в форме основной задачи таким образом: максимизировать функцию 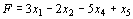 при условиях
при условиях
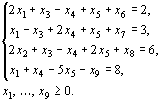
 2015-05-05
2015-05-05 346
346








