(4 семестр 2009г)
Опр.: Кольцо — система множеств, замкнутая относительно конечного объединения, пересечения и разности.
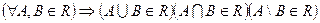 .
.
Опр.: Единицей E в системе множеств S называется такое множество, что какое бы множество A мы не выбрали, оно всегда содержится в E.
Опр.: Кольцо с единицей называется алгеброй.
Опр.: Кольцо замкнутое относительно счетных объединений называется 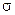 -кольцом.
-кольцом.
Опр.: Кольцо замкнутое относительно счетных пересечений называется 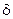 -кольцом.
-кольцом.
Опр.: 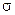 -кольцо с единицей называется
-кольцо с единицей называется 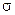 -алгеброй.
-алгеброй.
Опр.: 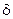 -кольцо с единицей называется
-кольцо с единицей называется 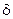 -алгеброй.
-алгеброй.
Лемма: Всякая 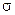 -алгебра является
-алгебра является 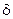 -алгеброй т наоборот.
-алгеброй т наоборот.
Теорема: Для всякой системы множеств S существует минимальное кольцо, содержащее эту систему. Такое кольцо единственно.
Опр.: Система множеств P называется полукольцом, если она обладает следующими свойствами:
1) 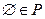
2) 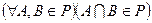
3) 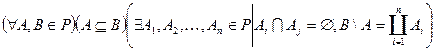
Теорема: Кольцо, порожденное полукольцом, состоит из всевозможных конечных объединений элементов полукольца. Кольцо, порожденное полукольцом, состоит из всевозможных конечных объединений непересекающихся попарно элементов полукольца.
Лемма: Пусть множество B содержит 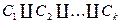 , тогда существует l
, тогда существует l 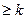 и множества
и множества 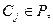
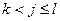 , таких что
, таких что 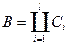 .
.
Теорема: Кольцо, порожденное полукольцом, состоит из всевозможных конечных объединений множеств полукольца.
Лемма: Даны два измеримых пространства 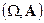 и
и 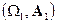 , и отображение
, и отображение 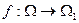 , тогда справедливо: Если
, тогда справедливо: Если 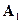 — полукольцо (кольцо, алгебра,
— полукольцо (кольцо, алгебра, 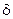 -алгебра), то
-алгебра), то 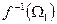 — полукольцо (кольцо, алгебра,
— полукольцо (кольцо, алгебра, 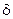 -алгебра), т.е. прообраз системы множеств есть такая же система как и ее образ.
-алгебра), т.е. прообраз системы множеств есть такая же система как и ее образ.
Опр.: Пусть имеется 2 пространства: 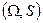 и
и 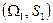 , и отображение
, и отображение 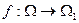 ,
,  называется
называется 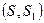 измеримым, если
измеримым, если 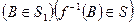 .
.
Свойство: Суперпозиция измеримых отображений измерима. Если  - измерима, а
- измерима, а 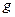 - борелевская, то
- борелевская, то 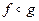 - измерима.
- измерима.
Теорема: (критерий измеримости) Пусть дано измеримое пространство 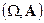 и отображение
и отображение 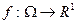 , тогда
, тогда  измерима, тогда и только тогда, когда
измерима, тогда и только тогда, когда 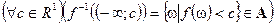 .
.
Лемма: Пусть 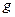 и
и  измеримые функции. Рассмотрим множество
измеримые функции. Рассмотрим множество 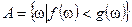 . Тогда множество
. Тогда множество 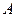 измеримо, т.е.
измеримо, т.е. 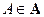
Свойства измеримых функций:
1) Если  измерима,
измерима, 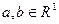 , то
, то 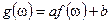 измерима, т.е. линейная функция от измеримой также измерима.
измерима, т.е. линейная функция от измеримой также измерима.
2) Пусть 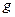 и
и  измеримы, тогда
измеримы, тогда 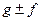
3) Пусть 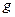 и
и  измеримы, тогда
измеримы, тогда 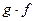
4) Пусть 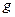 и
и  измеримы, тогда
измеримы, тогда 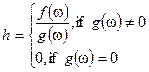 измерима.
измерима.
5) Из свойств 1 и 2 следует измеримость функции образующей линейное пространство.
6) Дано последовательность из измеримых функций 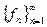 ,
,  , тогда
, тогда 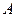 измеримо.
измеримо.
Опр.: Функцию будет называть ступенчатой, если она принимает конечное число значений. Простой, если она принимает не более, чем счетное число значений.
Лемма: Пусть  простая, тогда
простая, тогда  измеримая, тогда и только тогда, когда
измеримая, тогда и только тогда, когда 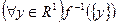 измерима.
измерима.
Теорема: Всякая измеримая функция является пределом последовательности простых измеримых функций.
Теорема: Всякая неотрицательная измеримая функция является пределом неубывающей последовательности ступенчатых функций.
Теорема: Пусть имеется 2 измеримые функции  и
и 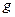 , и
, и 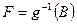 прообраз борелевской
прообраз борелевской 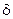 алгебры, и пусть
алгебры, и пусть  измерима в паре
измерима в паре  , тогда существует борелевская функция
, тогда существует борелевская функция 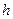 , т.ч.
, т.ч. 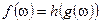
Опр.: Пусть дано некоторое множество 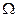 ,
, 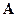 — система его подмножеств. Задано отображение
— система его подмножеств. Задано отображение 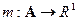 , тогда функция
, тогда функция 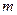 называется мерой, если она конечна, не отрицательна и
называется мерой, если она конечна, не отрицательна и 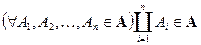
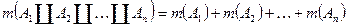 .
.
Свойства меры:
1) Если 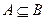 , то
, то 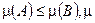 — мера.
— мера.
2) 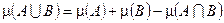 .
.
3) Дана последовательность множеств 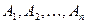 , тогда
, тогда 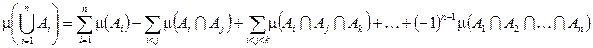 .
.
4) Если 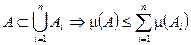 .
.
5) Пусть множества 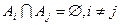 ,
, 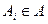 , тогда
, тогда 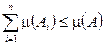 .
.
Опр.: Имеется пространство 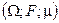 — измеримое пространство с мерой. Мера
— измеримое пространство с мерой. Мера 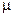 называется счетно-аддитивной на
называется счетно-аддитивной на 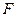 , если
, если 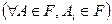
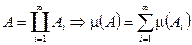 .
.
Свойства:
5’) 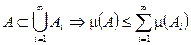
6’) если 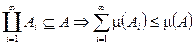
Лемма: Конечная аддитивная мера счетно-аддитивна, тогда и только тогда, когда она счетно-полуаддитивна.
Опр.: Семейство называется суммируемым, если его сумма конечна.
Свойства: 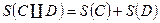 ;
; 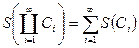 .
.
Свойство непрерывности меры: имеется измеримое пространство с мерой 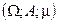 , которое счетно-аддитивно. Рассмотрим последовательность
, которое счетно-аддитивно. Рассмотрим последовательность 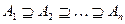 не возрастает и пусть
не возрастает и пусть 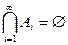 , тогда
, тогда 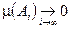 .
.
Другой вариант непрерывности:
Пусть 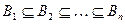 неубывающая последовательность множеств и
неубывающая последовательность множеств и 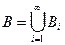 , тогда
, тогда 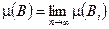 .
.
Опр.: Внешняя мера 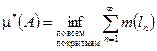 .
. 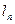 покрыто
покрыто 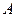 , если
, если 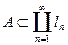 .
.
Свойства: 1) 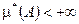 ; 2) если
; 2) если 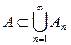 , то
, то 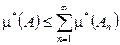 .
.
Опр.: Множество 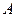 называется измеримым, если
называется измеримым, если 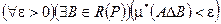 , где
, где 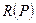 — кольцо, порожденное полукольцом. Расстоянием между множествами назовем
— кольцо, порожденное полукольцом. Расстоянием между множествами назовем 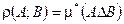 .
.
Свойства расстояния:
1) 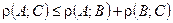 — правило треугольника.
— правило треугольника.
2) 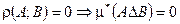 .
.
3) 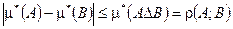 .
.
Свойства измеримых множеств:
1) Измеримые множества образуют кольцо.
2) Внешняя мера на кольце измеримых множеств является мерой.
3) Внешняя мера счетно-аддитивная на алгебре измеримых множеств.
4) Алгебра измеримых множеств является 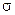 -алгеброй.
-алгеброй.
Опр.: Мерой Лебега называется мера, определенная на системе измеримых множеств 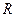 и совпадающая на
и совпадающая на 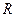 с внешней мерой.
с внешней мерой.
Теорема: 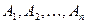 — измеримы и
— измеримы и 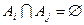 . Рассмотрим
. Рассмотрим 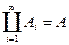 — измеримо
— измеримо 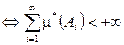 .
.
Опр.: Мера 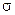 -конечной, если пространство
-конечной, если пространство 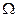 можно представить в виде объединения непересекающихся последовательностей множеств
можно представить в виде объединения непересекающихся последовательностей множеств 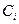 , таких, что
, таких, что 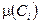 - конечно.
- конечно.
Опр.: Пусть 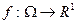 и
и  - измеримая и простая функция. Рассмотрим ряд
- измеримая и простая функция. Рассмотрим ряд 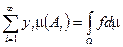 , если он сходится, то
, если он сходится, то  называется интегрируемой по Лебегу.
называется интегрируемой по Лебегу. 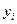 — значение
— значение  ,
, 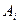 — прообраз
— прообраз 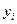 .
.
Свойства:
1) 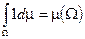 .
.
2) Если  интегрируемая и простая и
интегрируемая и простая и 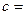 const,
const, 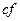 — интегрируемая функция, то
— интегрируемая функция, то 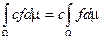 .
.
3) Если 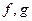 — простые и интегрируемые функции и их сумма простая и интегрируемая, то
— простые и интегрируемые функции и их сумма простая и интегрируемая, то 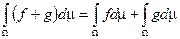 .
.
4) Аналогично для разности.
5) Если 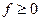 , то
, то 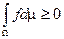 .
.
6) 4) и 5) и если 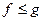 , тогда
, тогда 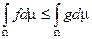 .
.
7) Пусть 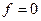 п.в. (почти всюду), тогда
п.в. (почти всюду), тогда 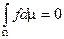 .
.
Лемма: Если  интегрируема, а
интегрируема, а 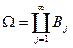 на каждом из множеств функция постоянна, тогда
на каждом из множеств функция постоянна, тогда 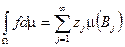 , где
, где 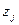 — необязательно различные значения функций на множествах постоянства
— необязательно различные значения функций на множествах постоянства 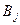 .
.
Опр.: Пусть  измерима, тогда
измерима, тогда  называется интегрируемой на измеримом множестве
называется интегрируемой на измеримом множестве 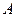 , если существует последовательность простых интегрируемых на множестве
, если существует последовательность простых интегрируемых на множестве 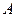 функций, равномерно сходящихся на
функций, равномерно сходящихся на 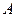 к
к  .
.
8) если 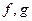 простые,
простые,  интегрируема и
интегрируема и 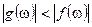 , то
, то 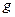 интегрируема.
интегрируема.
Лемма: Пусть  интегрируема на
интегрируема на 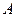 , тогда
, тогда 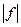 интегрируема на
интегрируема на 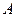 .
.
Лемма: Пусть 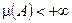 ,
, 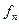 последовательность простых интегрируемых функций,
последовательность простых интегрируемых функций, 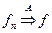 ,
, 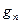 простые и
простые и 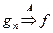 , тогда, начиная с некоторого номера,
, тогда, начиная с некоторого номера, 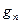 будет интегрируема.
будет интегрируема.
Лемма: Если  интегрируема на
интегрируема на 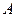 и
и 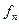 последовательность интегрируемых функций, которые равномерно сходятся к
последовательность интегрируемых функций, которые равномерно сходятся к  на
на 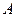 , то последовательность
, то последовательность  имеет предел.
имеет предел.
Лемма: Пусть даны 2 последовательности 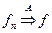 и
и 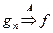 ,
, 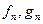 — простые и интегрируемые, тогда
— простые и интегрируемые, тогда 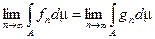 , т.е. предел не зависит от способа выбора последовательностей, равномерно сходящихся к
, т.е. предел не зависит от способа выбора последовательностей, равномерно сходящихся к  .
.
Опр.: Интегралом от интегрируемой функции  на множестве
на множестве 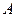 называется предел последовательности интегралов от простых функций, равномерно сходящихся к данной функции на множестве
называется предел последовательности интегралов от простых функций, равномерно сходящихся к данной функции на множестве 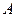 .
.
9) 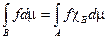 .
.
10) Неравенство Чебышева: Пусть 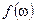 измеримая функция,
измеримая функция, 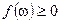 п.в. Рассмотрим множество
п.в. Рассмотрим множество 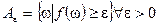 , тогда
, тогда 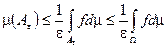 . Если какой-нибудь интеграл не существует, то он заменяется на
. Если какой-нибудь интеграл не существует, то он заменяется на 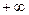 .
.
Следствие: Пусть 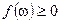 и
и 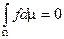 , тогда
, тогда 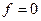 п.в.
п.в.
Свойство аддитивности интеграла Лебега: Пусть  интегрируемая на
интегрируемая на 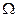 , тогда она интегрируема на любом измеримом подмножестве.
, тогда она интегрируема на любом измеримом подмножестве.
Свойство счетной аддитивности интеграла Лебега: Пусть 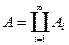 . Если
. Если  интегрируема на множестве
интегрируема на множестве 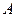 , то она интегрируема на любом измеримом подмножестве
, то она интегрируема на любом измеримом подмножестве 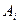 и
и 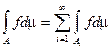 .
.
Теорема: (о равномерном предельном переходе под знаком интеграла Лебега): Пусть 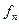 — последовательность не обязательно простых интегрируемых функций, равномерно сходящаяся на множестве
— последовательность не обязательно простых интегрируемых функций, равномерно сходящаяся на множестве 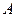 к функции
к функции  , тогда предельная функция интегрируема и
, тогда предельная функция интегрируема и 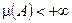 и
и 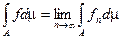 .
.
Виды сходимости:
0) Равномерная сходимость.
1) Сходимость всюду: 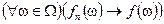 .
.
2) Сходимость почти всюду. Множество 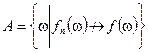 измеримо и
измеримо и 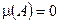 .
.
3) Сходимость по мере:  т.е.
т.е. 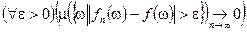 .
.
4) Сходимость в среднем порядка 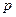 :
: 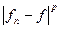 интегрируемая функция и
интегрируемая функция и 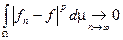 .
.
Теорема: Из равномерной сходимости следует сходимость всюду. Из сходимости всюду следует сходимость почти всюду. Из сходимости почти всюду следует сходимость по мере.
Опр.: Мера 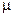 называется полной, если всякое подмножество множества
называется полной, если всякое подмножество множества 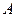 меры ноль измеримо. Само множество
меры ноль измеримо. Само множество 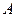 тоже имеет меру ноль.
тоже имеет меру ноль.
Теорема: Пусть 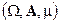 — измеримое пространство с мерой.
— измеримое пространство с мерой. 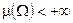 ,
, 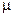 — полная. Пусть последовательно
— полная. Пусть последовательно 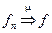 (сходится по мере), тогда существует последовательность
(сходится по мере), тогда существует последовательность 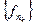 , которая сходится к
, которая сходится к  почти всюду.
почти всюду.
Теорема (Егорова): Пусть дано измеримое пространство с мерой 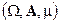 ,
, 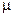 — полная,
— полная, 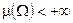 и последовательность
и последовательность 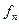 сходится к
сходится к  почти всюду, тогда
почти всюду, тогда 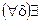 множество
множество 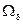 , мера дополнения которого
, мера дополнения которого 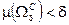 и
и 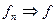 на
на 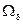 .
.
Теорема: (критерий сходимости почти всюду): Пусть 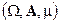 измеримое пространство с мерой.
измеримое пространство с мерой. 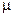 — полная,
— полная, 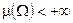 и последовательность
и последовательность 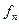 сходится к
сходится к  почти всюду, тогда, и только тогда, когда
почти всюду, тогда, и только тогда, когда 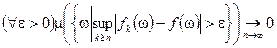 .
.
Опр.: Последовательность 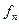 называется фундаментальной по мере, если
называется фундаментальной по мере, если 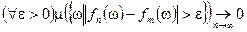
Утверждение: 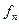 фундаментальна по мере, тогда, и только тогда, когда существует измеримая функция
фундаментальна по мере, тогда, и только тогда, когда существует измеримая функция  , к которой
, к которой 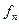 сходится по мере.
сходится по мере.
Опр.: 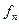 равномерно фундаментальна по мере, если
равномерно фундаментальна по мере, если 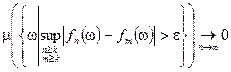 .
.
Утверждение: Последовательность 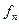 сходится почти всюду к некоторой измеримой функции, тогда, и только тогда, когда она равномерно фундаментальна по мере.
сходится почти всюду к некоторой измеримой функции, тогда, и только тогда, когда она равномерно фундаментальна по мере.
Теорема (Лебега): Пусть 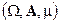 измеримой пространство с мерой,
измеримой пространство с мерой, 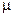 — полная,
— полная, 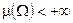 и последовательность,
и последовательность, 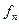 последовательность измеримых функций,
последовательность измеримых функций, 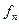 сходится к
сходится к  почти всюду,
почти всюду, 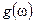 — измеримая и интегрируемая функция,
— измеримая и интегрируемая функция, 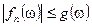 , тогда
, тогда 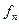 и
и  интегрируемы и
интегрируемы и 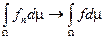 .
.
Теорема (Леви): Пусть 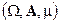 измеримой пространство с мерой,
измеримой пространство с мерой, 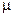 — полная,, имеется неубывающая последовательность функций
— полная,, имеется неубывающая последовательность функций 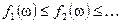 , которые интегрируемы и
, которые интегрируемы и 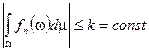 , тогда последовательность
, тогда последовательность 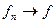 , которая конечна почти всюду и
, которая конечна почти всюду и 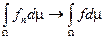 .
.
Следствие: Пусть 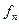 последовательность неотрицательных функций. Рассмотрим ряд
последовательность неотрицательных функций. Рассмотрим ряд 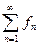 . Справедливо следующие равенство:
. Справедливо следующие равенство:  .
.
Теорема (Фату): Пусть имеется последовательность 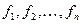 интегрируемых функций,
интегрируемых функций, 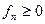 и существует
и существует 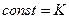 , т.ч.
, т.ч. 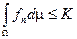 , тогда
, тогда 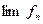 является конечным п.в. и справедливо неравенство
является конечным п.в. и справедливо неравенство 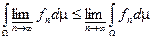 .
.
Теорема: (Связь между интегралом Лебега и интегралом Римана): Пусть 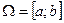 ,
,  ограничена и интегрируема по Риману, тогда
ограничена и интегрируема по Риману, тогда  интегрируема по Лебегу по мере
интегрируема по Лебегу по мере 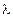 и верно следующие
и верно следующие 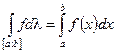 .
.
Опр.: Пусть имеется 2 измеримых пространства 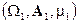 и
и 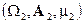 ,
, 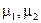 — полные конечные меры. Пусть
— полные конечные меры. Пусть 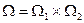 . Определим
. Определим 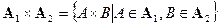 — это прямое произведение — полукольцо. Определим на этом полукольце меру
— это прямое произведение — полукольцо. Определим на этом полукольце меру 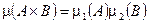 — произведение мер
— произведение мер 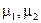 .
.
Теорема: (о плоской мере): Пусть имеются измеримые пространства с полной мерой 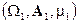 и
и 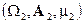 .
. 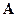 —
— 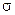 -алгебра. Рассмотрим измеримое множество
-алгебра. Рассмотрим измеримое множество 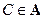 . Определим множество
. Определим множество 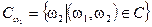 .
.
Пусть 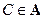 , тогда для почти всех
, тогда для почти всех 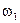 множества
множества 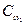 является измеримым, т.е.
является измеримым, т.е. 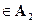 .
.
Функция 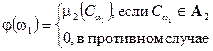 , тогда
, тогда 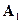 — измерима и интегрируема и.
— измерима и интегрируема и.
Следствие: Пусть 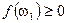 ,
, 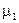 — измерима и интегрируема, тогда
— измерима и интегрируема, тогда 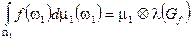 , где
, где 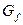 — подграфик функции
— подграфик функции  ,
, 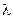 — мера Лебега.
— мера Лебега.
Теорема: (Фубини): пусть имеются 2 измеримых пространства 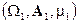 и
и 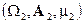 . Рассмотрим функцию 2х переменных
. Рассмотрим функцию 2х переменных 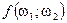 , она
, она 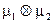 —измерима и интегрируема, тогда справедливы утверждения:
—измерима и интегрируема, тогда справедливы утверждения:
1) для почти всех 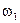 функция
функция 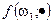 является
является 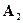 измеримой, интегрируемой относительно меры
измеримой, интегрируемой относительно меры 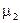 и
и 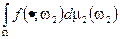 является измеримой функцией относительно алгебры
является измеримой функцией относительно алгебры 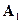 и интегрируемой по мере
и интегрируемой по мере 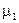 .
.
2) Справедливо равенство: (плоский интеграл можно заменить 2мя повторными): 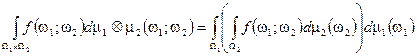 .
.
3) Аналогичные утверждения справедливы для интеграла взятого в обратном порядке.
Теорема: (обратная к теореме Фубини): пусть функция 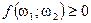 . Ее повторные интегралы существуеют и равны, тогда исходная функция интегрируема по прямому произведению мер и справедлива теорема Фубини.
. Ее повторные интегралы существуеют и равны, тогда исходная функция интегрируема по прямому произведению мер и справедлива теорема Фубини.
Следствие: Если повторный интеграл от модуля функции  конечен, тогда модуль
конечен, тогда модуль  и сама функция
и сама функция  интегрируемы и справедлива теорема Фубини.
интегрируемы и справедлива теорема Фубини.
Опр.: Функция 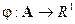 называется зарядом, если она обладает свойствами счетной аддитивности.
называется зарядом, если она обладает свойствами счетной аддитивности.
Теорема: Конечно аддитивная функция 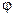 является зарядом, тогда, и только тогда, когда она непрерывна.
является зарядом, тогда, и только тогда, когда она непрерывна.
Замечание: Условие непрерывности заряда можно записать в терминах возрастающей последовательности Если 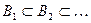 , то
, то 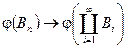 .
.
Опр.: 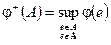 — положительная вариация заряда – конечная функция множества.
— положительная вариация заряда – конечная функция множества.
Теорема: Положительная вариация является счетно-аддитивной мерой.
Свойства: Заряд положительной вариации обладает свойством счетной полуаддитивности. Пусть 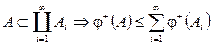 .
.
Опр.: рассмотрим функция 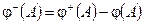 отрицательная вариация заряда, счетно-аддитивна и неотрицательна.
отрицательная вариация заряда, счетно-аддитивна и неотрицательна.
Разложение Жордана: 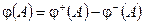 .
.
Опр.: Пусть 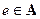 ,
, 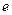 — множество положительности заряда
— множество положительности заряда 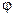 , если
, если 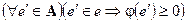 .
.
Пусть 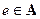 ,
, 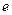 — множество отрицательности заряда
— множество отрицательности заряда 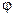 , если
, если 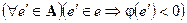 .
.
Теорема: (Хана): Пусть имеется заряд 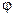 , тогда существует 2 множества:
, тогда существует 2 множества: 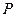 — множество положительности и
— множество положительности и 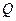 — множество отрицательности
— множество отрицательности 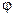 , т.ч.
, т.ч. 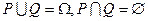 .
.
Лемма: (об исчерпывании): Пусть 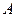 — множество.
— множество.
1) Пусть 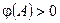 , тогда существует подмножество
, тогда существует подмножество 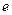 т.ч.
т.ч. 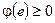 и
и 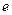 множество положительности.
множество положительности.
2) Пусть 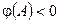 , тогда существует подмножество
, тогда существует подмножество 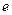 т.ч.
т.ч. 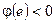 и
и 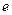 множество отрицательности.
множество отрицательности.
Лемма:
1) Счетное объединение множеств положительности заряда 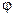 является множеством положительности.
является множеством положительности.
2) Счетное объединение множеств отрицательности заряда 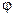 является множеством отрицательности.
является множеством отрицательности.
Следствие: Пусть 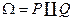 — разложение Хана, тогда
— разложение Хана, тогда 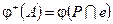 и
и 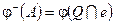 .
.
Опр.: имеется измеримое пространство с мерой 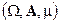 ,
, 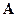 —
— 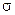 -алгебра
-алгебра 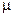 -измеримых множеств имеется заряд
-измеримых множеств имеется заряд 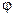 на
на 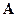 и эквиваленты следующие утверждения:
и эквиваленты следующие утверждения:
1) 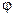 абсолютно непрерывен относительно меры
абсолютно непрерывен относительно меры 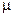 , если
, если 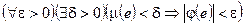 .
.
2) 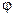 абсолютно непрерывен относительно меры
абсолютно непрерывен относительно меры 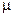 , если из того, что
, если из того, что 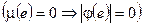 .
.
Теорема: (Радона-Никодима): Пусть 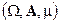 — измеримое пространство с мерой,
— измеримое пространство с мерой, 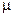 — полная. Пусть
— полная. Пусть 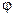 заряд.
заряд. 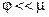 (абсолютно непрерывен относительно меры
(абсолютно непрерывен относительно меры 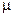 ), тогда существует
), тогда существует 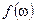 — измеримая и интегрируемая на
— измеримая и интегрируемая на 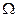 , т.ч.
, т.ч. 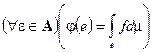 и
и 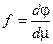 —производная Радона-Никодима.
—производная Радона-Никодима.
Лемма: (2я лемма об исчерпывании): Пусть 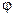 мера,
мера, 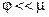 и
и 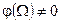 (не тривиальная мера), тогда существует мера
(не тривиальная мера), тогда существует мера 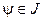 , т.ч.
, т.ч. 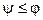 .
.
Опр.: мера 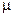 сингулярна мере
сингулярна мере 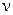 (
(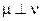 ), если существует множество
), если существует множество 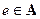 , для которого выполнено условие:
, для которого выполнено условие: 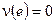 и
и 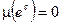 .
.
Теорема (о разложении): Пусть 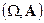 — измеримое пространство с мерой
— измеримое пространство с мерой 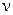 ,
, 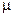 мера на
мера на 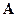 , тогда ее можно представить в виде:
, тогда ее можно представить в виде: 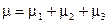 , где
, где 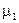 — дискретная мера,
— дискретная мера, 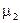 мера, абсолютно непрерывная относительно
мера, абсолютно непрерывная относительно 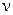 ,
, 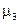 — мера, сингулярная относительно
— мера, сингулярная относительно 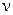 .
.
Опр.: Пусть имеется измеримое пространство с полной мерой 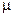
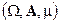 . Функция
. Функция  суммируема со степенью
суммируема со степенью 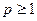 , если
, если 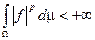 . Пространство суммируемых функций обозначим через
. Пространство суммируемых функций обозначим через 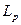 .
.
Неравенство Гельдера: 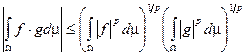 .
.
Неравенство Миньковского: 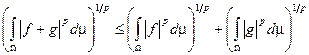 .
.
Опр.: На пространстве 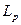 определим функционал
определим функционал 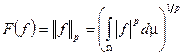 .
.
Свойства:
1) 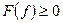 .
.
2) 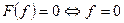 п.в.
п.в.
3) 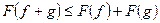 .
.
4) 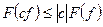
5) 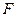 полунорма, если
полунорма, если 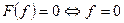 всюда, то
всюда, то 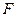 — норма.
— норма.
Опр.: Пусть имеется абстрактное множество 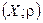 причем
причем 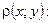
1) 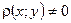
2) 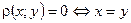
3) 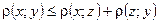 ,
,
тогда 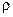 называется метрикой,
называется метрикой, 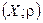 метрическим пространством.
метрическим пространством.
Опр.: метрическое пространство называется полным, если в нем всякая фундаментальная последовательность имеет предел.
Теорема: (критерий полноты): Пусть 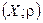 метрическое пространство с метрикой
метрическое пространство с метрикой 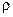
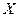 полное, тогда, и только тогда, когда для любой последовательности
полное, тогда, и только тогда, когда для любой последовательности 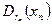 замкнутых, вложенных друг в друга шаров, радиус которых
замкнутых, вложенных друг в друга шаров, радиус которых 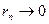 имеет непустое пересечение.
имеет непустое пересечение.
Опр.: Пространство 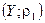 называется пополнением пространства
называется пополнением пространства 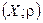 , если существует инъективное отображение
, если существует инъективное отображение 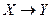 обладающее свойствами:
обладающее свойствами:
1)  сохраняет расстояние, т.е.
сохраняет расстояние, т.е. 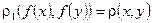 .
.
2) Образ 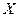 всюду плотен в
всюду плотен в 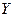 .
.
Теорема: (о пополнении): Всякое метрическое пространство имеет пополнение.
Опр.: Пусть 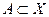 ,
, 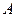 называется выпуклым, если
называется выпуклым, если 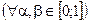 т.ч,
т.ч, 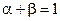 и
и 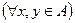
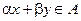 .
.
Опр.: Множество 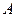 называется абсолютно выпуклым, если
называется абсолютно выпуклым, если 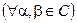 т.ч,
т.ч, 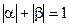 и
и 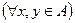
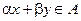 .
.
Опр.: Пусть имеется функционал 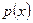 вещественнен на
вещественнен на 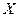 (линейное пространство), он называется выпуклым функционалом, если выполнены условия:
(линейное пространство), он называется выпуклым функционалом, если выполнены условия:
1) 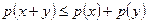
2) 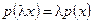
Утверждение: Всякое абсолютно выпуклое множество является выпуклым.
Опр.: Функционал 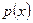 называется абсолютно выпуклым функционалом, если выполнены условия:
называется абсолютно выпуклым функционалом, если выполнены условия:
1) 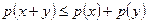
2) 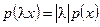 .
.
Опр.: Абсолютно-выпуклый функционал называется нормой, если 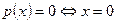 .
.
Утверждение: Если 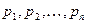 — полунормы, то
— полунормы, то 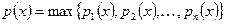 также полунорма.
также полунорма.
Теорема: Пусть 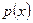 выпуклый неотрицательный функционал, тогда справедливы:
выпуклый неотрицательный функционал, тогда справедливы:
1) 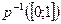 выпуклый и поглощающий
выпуклый и поглощающий
2) Если 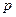 полунорма и
полунорма и 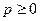 , то
, то 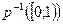 абсолютно выпуклый.
абсолютно выпуклый.
3) 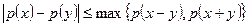
4) 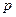 полунорма, тогда
полунорма, тогда 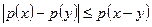 .
.
Опр.: Пусть 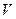 выпуклое, поглощающее множество в пространстве
выпуклое, поглощающее множество в пространстве 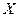 . Рассмотрим функционал
. Рассмотрим функционал 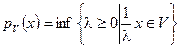 . Назовем его функционалом Миньковского.
. Назовем его функционалом Миньковского.
Свойства: (теорема Формула Миньковского):
1) 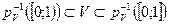
2) 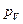 — выпуклый функционал.
— выпуклый функционал.
3) Если 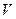 абсолютно выпуклый, то
абсолютно выпуклый, то 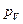 полунорма.
полунорма.
Опр.: имеется некоторое множество 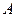 , которое частично упорядочено (обозначим
, которое частично упорядочено (обозначим 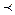 ). Множество
). Множество 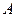 называется направлением, если
называется направлением, если 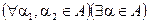 , которое
, которое 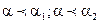 .
.
Опр.: Пусть 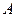 направление,
направление, 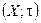 топологическое пространство. Рассмотрим семейство
топологическое пространство. Рассмотрим семейство 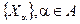 . Оно называется обобщенное последовательностью.
. Оно называется обобщенное последовательностью. 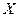 называется пределом обобщенной последовательности
называется пределом обобщенной последовательности 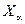 , если для любого открытого множества
, если для любого открытого множества 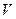 существует
существует 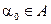 , т.ч.
, т.ч. 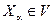 при
при 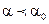 .
.
Некоторые обозначения не соответствуют обозначениям тетради.
©Богданов Игорь, 2010
 2015-05-05
2015-05-05 2037
2037