Пропускная способность симметричного канала со стиранием

Рассмотренную выше систему связи можно усовершенствовать, введя «защитный интервал» или «зону стирания». При µ > ρ +Δ решение принимается в пользу 1, а при µ < ρ - Δ принимаются решение в пользу 0. При ρ –Δ < µ < ρ +Δ символ искажается настолько, что становится «неузнаваемым». Получаем модель бинарного симметричного канала со стиранием символа (Б.С.К.С.). Это небольшое изменение заметно повышает эффективность системы, поскольку задача исправления стираний проще задачи исправления ошибок. Один и тот же корректирующий код позволяет исправить примерно в два раза больше стираний, чем ошибок.

Перейдем к моделированию Б.С.К.С. Рассмотрим двоичный канал (на входе сигналы u₁ и u₂ с вероятностями появления p(u₁) и p(u₂), соответственно). На приемном конце канала связи любой из них с вероятностью p может быть интерпретирован как противоположный (см. предыдущий раздел), но, помимо этого, с вероятностью q искажения в канале оказываются такими, что принятый знак не идентифицируется ни с одним из поступающих на вход. В таком случае можно считать, что принят новый сигнал v₃, появление которого можно интерпретировать как пропажу (стирание) входного сигнала – по этой причине канал назван двоичным симметричным со стиранием. Тогда

P(v₁|u₁) = P(v₂|u₂) = 1 – p – q, P(v₂|u₁) = P(v₁|u₂) = p, P(v₃|u₁) = P(v₃|u₂) = q,

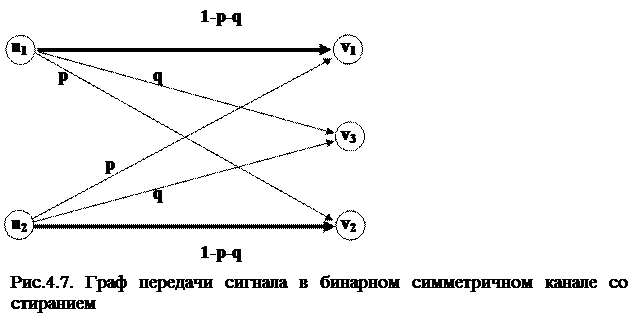Эту же систему можно представить в виде марковской цепи с матрицей переходных вероятностей.

P(v|u)	v1	v2	v3
u1	1-p-q	p	q
u2	p	1-p-q	q

Расчет условной энтропии шума в соответствии с формулой (4.10) дает:

H(v|u) = -P(u₁)∙(P(v₁|u₁)∙log₂P(v₁|u₁) + P(v₂|u₁)∙log₂P(v₂|u₁) + P(v₃|u₁)∙log₂P(v₃|u₁)) – -P(u₂)∙(P(v₁|u₂)∙log₂P(v₁|u₂) + P(v₂|u₂)∙log₂P(v₂|u₂) + P(v₃|u₂)∙log₂P(v₃|u₂)).

Подставляя вероятности из матрицы переходных вероятностей, получим:

H(v|u) = -P(u₁)∙((1-p-q)∙log₂(1-p-q) + p∙log₂p + q∙log₂q) –

- P(u₂)∙(p∙log₂p + (1-p-q)∙log₂(1-p-q) + q∙log₂q) =

-(P(u₁) + P(u₂))∙((1-p-q)∙log₂(1-p) + p∙log₂p + q∙log₂q)) = |в силу того, что P(u₁)+P(u₂)=1| = -(1-p-q)∙log₂(1-p-q) – p∙log₂p – q∙log₂q.

Таким образом, в силу (4.8)

I(u,v) = H(v) + (1-p-q)∙log₂(1-p-q) + p∙log₂p + q∙log₂q.

Поскольку H(v|u) не зависит от значений априорных вероятностей, взаимная информация I(u,v) достигает максимума при таких вероятностях, когда наибольшее значение приобретает энтропия H(v). Для нахождения H(v) необходимо знать вероятности всех сигналов, появляющихся на выходе из канала (обозначим эти вероятности q_j (j = 1,2,3)).

Вероятность появления v₃ (то есть стирания символа) уже установлена: q₃ = q. Для v₁ вероятность q₁ = p(u₁)·(1 – p – q) + p(u₂)·p; аналогично для v₂ находим q₂ = p(u₂)·p + p(u₂)·(1 – p – q). Тогда по формуле (4.9)

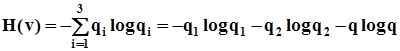
Поскольку q определяется особенностями канала и не зависит от априорных вероятностей сигналов на входе, наибольшая энтропия выхода H(v) будет при максимальном значении выражения – q₁·log₂q₁ – q₂·log₂q₂, причем, при любых p(u₁) и p(u₂) справедливо q₁ + q₂ = 1 – q (так как Σ q = 1) Можно показать (аналогично доказательству третьего свойства энтропии), что указанное выражение достигает максимума при условии q₁ = q₂ = 0,5·(1 – q). Тогда

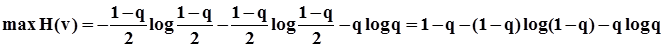
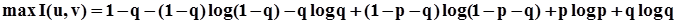приведя подобные, получим:

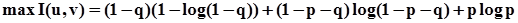
Окончательно для пропускной способности двоичного симметричного канала со стиранием имеем:

C = C₀((1-q)∙(1-log₂(1-q)) + (1-p-q)∙log₂(1-p-q) + p∙log₂p) (4.16)

Проанализируем полученный результат. С = С(p,q), причем, C будет уменьшаться при увеличении как p, так и q. Если вероятности p и q отличны от 0, то, как видно из полученного выражения, C < C₀. В реальных двоичных каналах со стиранием p < q, т.е. вероятность такого искажения входного сигнала, при котором его невозможно распознать, выше вероятности такого искажения, при котором сигнал становится похожим на второй из используемых сигналов. В тех ситуациях, когда p пренебрежимо мала и единственным искажением оказывается стирание сигнала, пропускная способность оказывается равной: C = С₀∙(1 – q). График этой функции представлен на рис.4.8.

Полученный результат представляется вполне закономерным: при p = 0 из V двоичных сигналов, передаваемых по каналу за единицу времени, в среднем V·q будет «стираться», но при этом остальные V·(1– q) сигналов будут на приемном конце расшифровываться без потерь, и с каждым из них связан ровно 1 бит информации.

Заканчивая рассмотрение характеристик реального дискретного канала передачи информации, мы можем сделать следующие заключения.

Помехи, существующие в реальном канале связи, приводят к снижению его пропускной способности (по сравнению с аналогичным каналом без помех).

Пропускная способность реального канала может быть рассчитана по известным априорным и апостериорным вероятностям. Для их определения требуются статистические исследования передачи информации в канале.