Рассмотрим работу достаточно типичной системы связи, в которой информация передается двоичными сигналами «0» и «1», имеющими разные уровни квантования. Приемное устройство анализирует выход канала в течение промежутка времени, соответствующего длительности элементарного сигнала и вычисляет некоторую скалярную величину µ (уровень принятого сигнала). Решение принимается сравнением µ с некоторым порогом ρ. При µ > ρ принимается решение в пользу «1», в противном случае, при µ < ρ, решением будет «0». При правильном выборе порога ρ вероятности ошибок при передаче сигналов будут одинаковыми, и мы приходим к модели бинарного симметричного канала с инверсией (Б.С.К.И.) Недостаток такой простейшей схемы приема состоит в том, что демодулятор теряет информацию о надежности принимаемых сигналов. Очевидно, значениям µ ≈ ρ соответствуют ненадежные решения, и эти сведения могут быть полезными при последующей обработке информации.
Сформулируем модель Б.С.К.И. Пусть на вход канала подаются сигналы двух типов (u1 и u2 – например, импульс и пауза) и они же принимаются на выходе, т.е. {u} = {v}, Nu = Nv. Безошибочный прием сигнала означает, что при посылке u1 принимается v1, а при посылке u2 принимается v2.
Пусть, далее, вероятность ошибки передачи для обоих типов сигналов одинакова и равна p; тогда, вероятность безошибочной передачи равна 1 - p. То есть можно записать:
P(v1|u1) = P(v2|u2) = 1 – p; P(v2|u1) = P(v1|u2) = p,
В виде графа такой канал можно представить так:
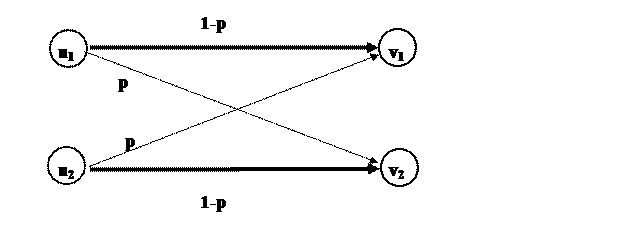 |
Рис.4.5. Граф передачи сигнала в бинарном симметричном канале с инверсией
Линии со стрелками указывают, в какие принимаемые сигналы могут перейти те, что отправлены на входе; рядом со стрелками указаны вероятности соответствующих переходов. Эту же систему можно представить в виде матрицы переходов марковской цепи с переходными вероятностями:
| P(v|u) | v1 | v2 |
| u1 | 1-p | p |
| u2 | p | 1-p |
Такой канал называется двоичным симметричным.
Найдем пропускную способность канала. Потребуется вычислить I(u,v), найти скорость передачи информации и установить ее максимум как функции от вероятности ошибки р.
I(u,v) = H(v) – H(v|u)
Вычислим энтропию принятого сигнала:
H(v) = - P(v1)∙log2P(v1) – P(v2)∙log2P(v2)
и энтропию шума:
H(v|u) = -P(u1)∙(P(v1|u1)∙log2P(v1|u1) + P(v2|u1)∙log2P(v2|u1)) – P(u2)∙(P(v1|u2)∙log2P(v1|u2) + P(v2|u2)∙log2P(v2|u2)).
Подставляя вероятности из матрицы перехода, получим:
H(v|u) = -P(u1)∙((1-p)∙log2(1-p) + p∙log2p) - P(u2)∙(p∙log2p + (1-p)∙log2(1-p)) =
= -(P(u1) + P(u2))∙((1-p)∙log2(1-p) + p log2p)) = -(1-p)∙log2(1-p) – p∙log2p)
При заданных вероятностях ошибок энтропия H(v|u) – величина постоянная. Максимум скорости передачи информации можно искать, варьируя вероятностями P(vi). Известно, что для бинарной системы энтропия будет максимальна, если сигналы равновероятны, и равна при этом 1, то есть H(v) = 1. Значит, пропускная способность будет равна
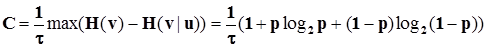 (4.14)
(4.14)
График функции С(р) изображен на рисунке 4.6.
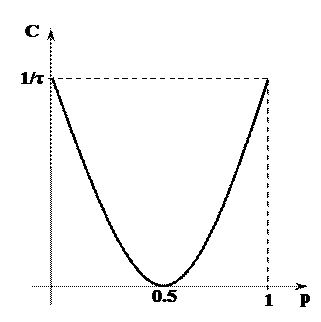
Рис. 4.6. Зависимость пропускной способности от вероятности ошибок.
Максимального значения равного 1/τ функция C достигает при p = 0 (очевидно, это означает отсутствие помех) и при p = 1, что соответствует ситуации, когда канал полностью инвертирует входные сигналы (т.е. заменяет 0 на 1, а 1 на 0) - это не служит препятствием для однозначной идентификации посланного сигнала по принятому и, следовательно, не снижает пропускной способности канала. Во всех остальных ситуациях (т.е. при 0 < p < 1) верно неравенство C < 1/τ. Наконец, при p = 0.5 пропускная способность становится равной 0 – это вполне естественно, поскольку вероятность искажения 0.5 означает, что независимо от того, какой сигнал был послан, на приемном конце с равной вероятностью может появиться любой из двух допустимых сигналов. Ясно, что передача в таких условиях оказывается невозможной.
Поскольку канал двоичный, 1/τ = 1/τ0 = C0 (так обозначим идеальную пропускную способность, то есть пропускную способность двоичного канала без помех). Произведя соответствующую замену, получим:
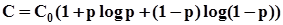 (4.15)
(4.15)
Выражение в скобках не превышает 1, следовательно, справедливо соотношение: С ≤ C0, т.е. можно считать доказанным, что наличие помех снижает пропускную способность (и даже может сделать ее равной 0).
 2015-05-05
2015-05-05 2165
2165
