Полная фаза и мгновенная частота. Сигналы с угловой модуляцией

Введение

Рассмотрим применение теории комплексной огибающей для формирования сигналов с угловой модуляцией, у которых будет изменятся фаза 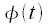радиосигнала, а амплитуда 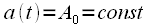остается постоянной.

Полная фаза и мгновенная частота. Сигналы с угловой модуляцией

Для начала вспомним понятие полной фазы радиосигнала

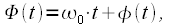
(1)

а также понятие мгновенной частоты радиосигнала, как производной от полной фазы:

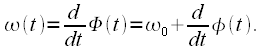
(2)

Сигналы у которых изменяется полная фаза в соответствии с модулирующим сигналом называются сигналами с угловой модуляцией.

Для начала рассмотрим сигналы с фазовой модуляцией (phase modulation PM). У сигналов с PM полная фаза изменяется в соответствии с модулирующим сигналом:

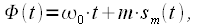
(3)

где 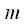называется индексом фазовой модуляции или девиацией фазы, а модулирующий сигнал по модулю не превосходит единицы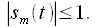

Тогда комплексная огибающая PM сигнала имеет вид:

(4)

а сам радиосигнал может быть представлен следующим образом:

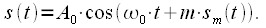
(5)

Теперь рассмотрим сигнал с частотной модуляцией (frequency modulation FM). В отличии от PM при частотной модуляции происходит изменение мгновенной частоты радиосигнала:

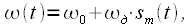
(6)

где 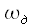называется индексом частотной модуляции или девиацией частоты, а модулирующий сигнал по модулю не превосходит единицы 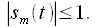Тогда полную фазу радиосигнала можно рассчитать как интеграл от мгновенной частоты:

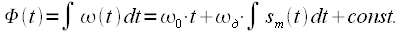
(7)

Сигнал с FM имеет вид:

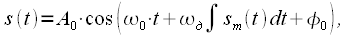
(8)

где 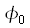- произвольная постоянная интегрирования полной фазы (8). Обратите внимание, что абсолютно не верно подставлять выражение для мгновенной частоты вместо несущей частоты в выражение для полосового сигнала:

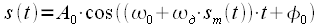
(9)

так как 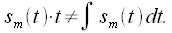Правильным является выражение (9)!