Рассмотрим элементарный случай, когда входящий поток – простейший, продолжительность обслуживания экспоненциальная, места для ожидания в очереди отсутствуют. Анализ может быть проведен с использованием теории Марковских процессов.
Введем множество возможных состояний системы:
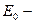 все каналы системы свободны;
все каналы системы свободны;
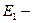 один канал занят, остальные свободны;
один канал занят, остальные свободны;
……………………………………………………………………………
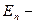 все n каналов системы заняты.
все n каналов системы заняты.
Будем считать, что интенсивность входящего потока заявок равна 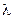 , а закон распределения продолжительности обслуживания имеет вид
, а закон распределения продолжительности обслуживания имеет вид 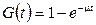 , где
, где 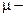 интенсивность обслуживания выражает количественно среднее число заявок, которое каждый канал системы в состоянии обслужить
интенсивность обслуживания выражает количественно среднее число заявок, которое каждый канал системы в состоянии обслужить
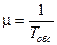 ,
, 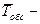 среднее время обслуживания.
среднее время обслуживания.
Нарисуем граф переходов системы
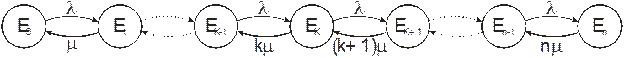
Система дифференциальных уравнений для вероятностей состояний имеет вид:
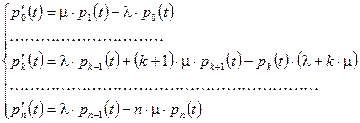
Систему уравнений необходимо дополнить условием нормировки 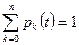 . Для решения системы используют преобразование Лапласа. При этом получим следующую систему линейных алгебраических уравнений:
. Для решения системы используют преобразование Лапласа. При этом получим следующую систему линейных алгебраических уравнений:
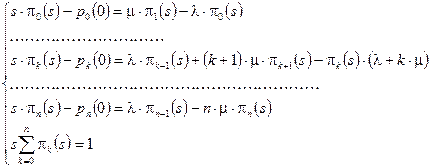
Решив эту систему уравнений и выполнив обратное преобразование Лапласа, получим соотношение для 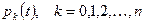 . Для оценки эффективности СМО интерес представляет асимптотическое поведение систему при
. Для оценки эффективности СМО интерес представляет асимптотическое поведение систему при 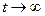 . В этом случае процесс в системе приобретает установившийся характер и поэтому
. В этом случае процесс в системе приобретает установившийся характер и поэтому 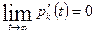 . Тогда уравнения системы упрощаются к виду:
. Тогда уравнения системы упрощаются к виду:
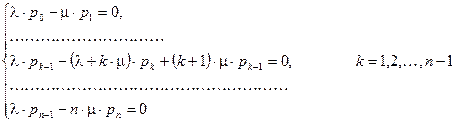
Введем переменную 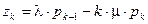 . Тогда
. Тогда
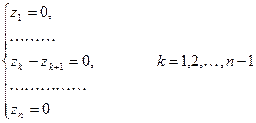
Откуда легко видеть, что 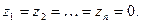 Поэтому
Поэтому 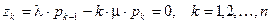
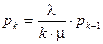 .
.
Тогда
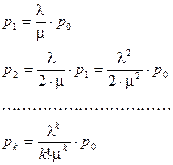
Таким образом, вероятности всех состояний выражены через 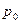 . Для расчета
. Для расчета 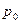 используем условие нормировки.
используем условие нормировки.
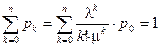
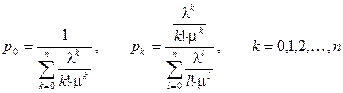
Введем параметр 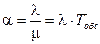 , который называется приведенной интенсивностью входного потока. Тогда
, который называется приведенной интенсивностью входного потока. Тогда
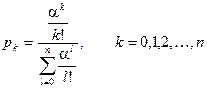
Эти соотношения называются формулами Эрланга. С использованием этих формул легко рассчитать вероятность отказа системы
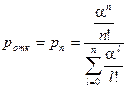
Можно найти относительную пропускную способность – вероятность того, что заявка будет обслужена
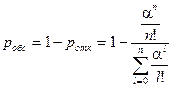
Абсолютную пропускную способность получим, умножая интенсивность потока заявок 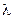 на
на 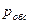 :
: 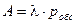 .
.
Среднее число занятых каналов можно найти, как математическое ожидание дискретной случайной величины с возможными значениями 0,1,…,n и вероятностями этих значений 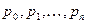
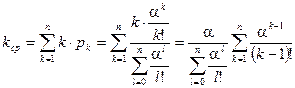
Введем 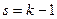 . Тогда
. Тогда
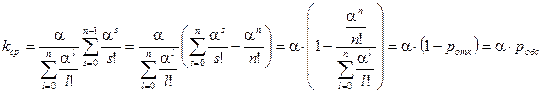
С другой стороны, среднее число занятых каналов можно найти по другому. Абсолютная пропускная способность 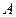 - это интенсивность потока обслуженных системой заявок. Каждый занятый канал в единицу времени обслуживает в среднем
- это интенсивность потока обслуженных системой заявок. Каждый занятый канал в единицу времени обслуживает в среднем 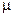 заявок. Значит среднее число занятых каналов равно:
заявок. Значит среднее число занятых каналов равно:
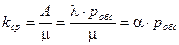 .
.
 2015-05-06
2015-05-06 1054
1054








