Составление расчетных динамических схем машин и механизмов. Приведение сил, масс, моментов инерции, жесткостей

Динамический расчет начинают с составления расчетной динамической схемы машины и уравнений движения масс, входящих в эту схему. От реальной машины к расчетной динамической схеме переходят, пренебрегая теми физическими факторами, которые для конкретного расчетного режима имеют несущественное значение.

Выбор той или иной расчетной схемы определяется задачей расчета. В расчетных динамических схемах реальные параметры машин (масса, коэффициенты жесткости, податливости и т.п.), а также внешние нагрузки заменяют приведенными величинами для упрощения расчетных уравнений и соот ношений. Приведение параметров и нагрузок производят на основании равенства общей энергии приведенной системы. Приведение производится либо к поступательному движению, либо к вращательному движению одной из масс механизма.

Критерием достоверности принятой расчетной схемы является опыт, сравнение теоретического расчета с результатами эксперимента.

Приведенные силы определяют из условия равенства их работы сумме работ тех сил, которые они заменяют, т.е.

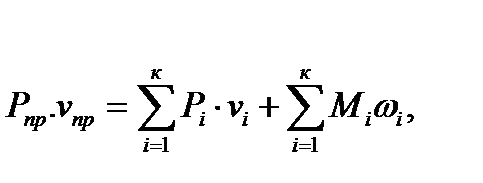
где 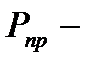приведенная сила; 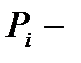проекция действующей на i-e звено силы на направление движения центра масс этого звена; 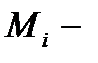момент, действующий на i-e звено.

Из этого уравнения находим:

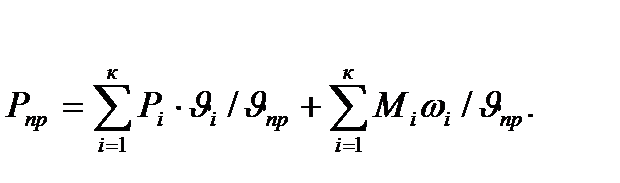(2.1)

Приведенная масса и приведенный момент инерции определяются из условия равенства кинетической энергии приведенной массы сумме кинетических энергий масс, которые она заменяет. Аналитически это правило выражается уравнениями:

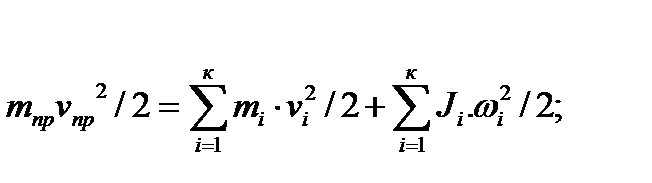
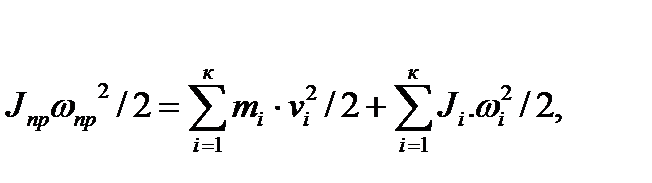
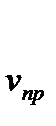где m_пр и J_{пр -}приведенная масса и приведенный момент инерции; и 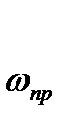-линейная и угловая скорости звена приведения; m _i uJ _i - масса и момент инерции i- го звена механизма; 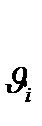и 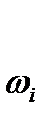-линейная и угловая скорости i -го звена механизма.

Из этих уравнений находим

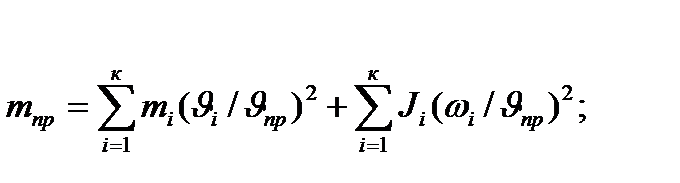(2.2)

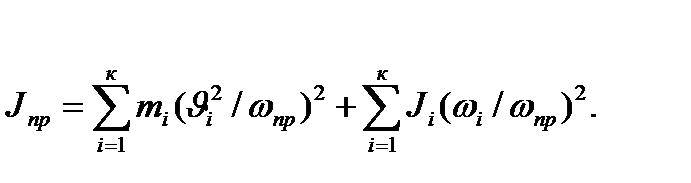(2.3)

Приведение жесткостей выполняется так, чтобы потенциальная энергия приведенной системы равнялась потенциальной энергии реальной упругой системы.

Пусть имеется система из двух валов с жесткостью C₁ и С₂, соединенных между собой зубчатой передачей(рис. 2.1, a), которую требуется заменить системой с одним упругим элементом, имеющим приведенную жесткость С_пр (рис.2.1, b), причем, жесткости следует привести к валу 1.

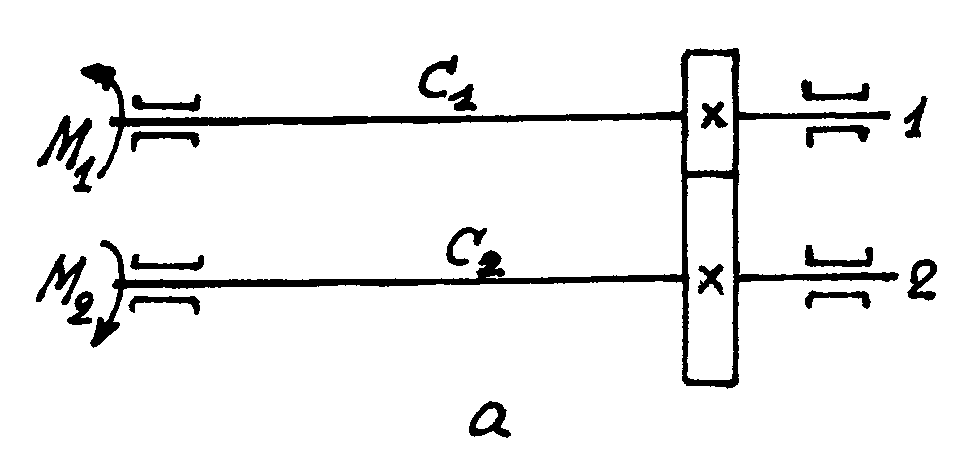
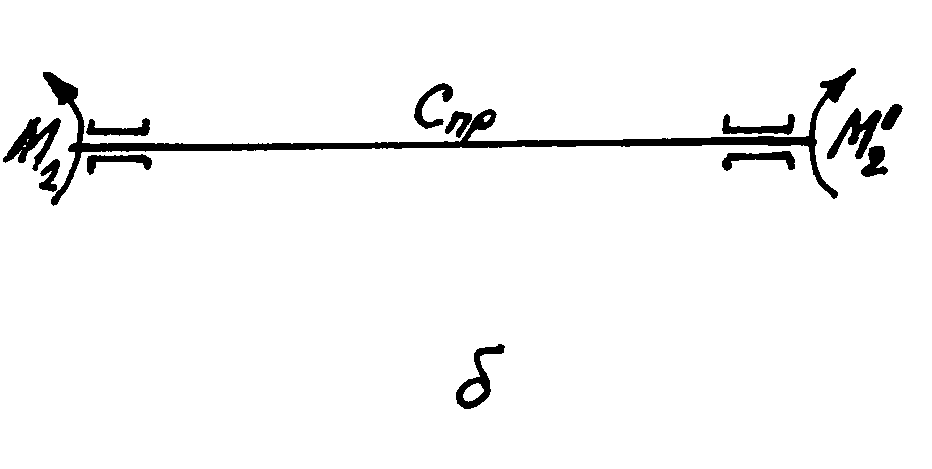
Рисунок 2.1 - Схема к приведению жесткостей двух валов с зубчатой передачей к жесткости одного вала

Если к валу 1 приложен момент M₁, то момент, приложенный к валу 2, M_{2 =} M₁^.U; в приведенной системе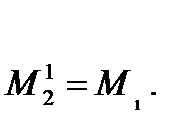

В нашем примере: потенциальная энергия реальной системы

П = М₁^.φ₁ /2 + М₂^. φ ₂ /2 = М₁(φ ₁ + φ ₂^.U) /2,

где φ₁, φ₂^.- углы закручивания валов под действием приложенных к ним моментов, причем φ₁ = M₁/C₁; φ₂ = M₂/C₂; U - передаточное число зубчатой передачи.

Потенциальная энергия приведенной системы

П = М₁^. φ _пр /2,

где φ _пр - угол закручивания приведенной системы.

Приравнивая два выражения потенциальной энергии, получаем

φ _пр = φ ₁ + φ ₂^.U. (2.4)

Согласно определению, приведенная жесткость

C_пр= М₁/ φ _пр = М₁/(φ ₁ + φ ₂^.U).

Подставляя в это уравнение значения М₁ = φ₁^.С₁ и φ _{2 =} φ ₁C₁U/C₂,

получаем 1/C_пр = 1/C₁ + U²/C₂ или C_пр = C₁ ^. C₂ / (С₁U² + C₂). (2.5)

Основная литература [3, c. 319…325]

Дополнительная литература [10, c. 34…36]

Контрольные вопросы:

1. Сколько масс и какой способ соединения между ними должна содержать расчетная динамическая схема?

2. К какому виду движения одной из масс механизма производится приведение параметров машин и внешних нагрузок?

3. Приведите зависимости для определения приведенных сил, масс, моментов инерции и жесткостей.

Лекция 3