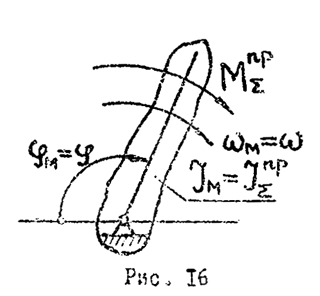
Механизм представляет собой сложную систему звеньев, нагруженных различными силами и моментами. Чтобы упростить определение закона движения такой сложной системы, применяют метод приведения сил и масс, который позволяет заменить реальный механизм некоторой эквивалентной (расчетной) схемой - одномассовой динамической моделью механизма (рис. 16). Вращающееся звено динамической модели двинется так, что его координата 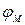 совпадает в любой момент времени с координатой
совпадает в любой момент времени с координатой 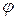 начального звена механизма (обобщенной координатой механизма):
начального звена механизма (обобщенной координатой механизма): 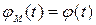 . К звену модели приложен приведенный момент сил
. К звену модели приложен приведенный момент сил 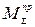 , а момент инерции
, а момент инерции 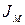 этого звена относительно оси вращения является суммарным приведенным моментом инерции механизма
этого звена относительно оси вращения является суммарным приведенным моментом инерции механизма 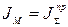 .
.
а) метод приведения, сил и моментов пар сил
 Суммарный приведенный момент
Суммарный приведенный момент 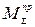 заменяет все силы и моменты, приложенные к различным звеньям механизма, и равен
заменяет все силы и моменты, приложенные к различным звеньям механизма, и равен
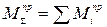 (24)
(24)
Величина каждого 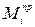 определяется из условия равенства элементарных работ действительной силы (или момента) и приведенного момента на возможных перемещениях. Приведенный момент
определяется из условия равенства элементарных работ действительной силы (или момента) и приведенного момента на возможных перемещениях. Приведенный момент 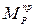 , заменяющий действительную силу P, приложенную в точке K некоторого звена механизма, определяется по формуле
, заменяющий действительную силу P, приложенную в точке K некоторого звена механизма, определяется по формуле
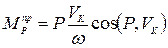 (25)
(25)
где 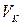 - линейная спорость точки K приложения силы;
- линейная спорость точки K приложения силы;
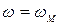 - угловая скорость звена динамической модели, равная угловой скорости начального звена механизма.
- угловая скорость звена динамической модели, равная угловой скорости начального звена механизма.
Отношение скоростей 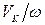 м/рад в литературе называют аналогом линейной скорости точки K, или передаточной функцией.
м/рад в литературе называют аналогом линейной скорости точки K, или передаточной функцией.
Приведенный момент 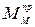 , заменяющий действительный момент M, приложенный к i -му звену механизма, определяется по формуле
, заменяющий действительный момент M, приложенный к i -му звену механизма, определяется по формуле
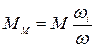 (26)
(26)
где 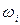 - угловая скорость i -ого звена.
- угловая скорость i -ого звена.
Отношение угловых скоростей 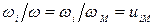 передаточная функция (передаточное отношение).
передаточная функция (передаточное отношение).
Знак приведенного момента определяется знаком действительной силы: если действительная сила (или момент) положительна, т.е. совершает положительную работу, то и приведенный момент положителен, т.е. направлен по угловой скорости звена динамической модели. Следовательно, в формуле (25) 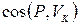 берется по абсолютной величине.
берется по абсолютной величине.
Отношения скоростей зависят от положения механизма, а не от скорости его движения. Следовательно, приведение сил может выполняться без знания действительного закона движения звеньев.
Пример. Рассмотрим определение приведенных моментов, заменяющих действительные силы и моменты, приложенные к звеньям механизма двухцилиндрового двигателя (см. рис. 13). К данному механизму приложены 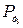 и
и 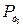 - движущие силы, действующие на звенья 3 и 5;
- движущие силы, действующие на звенья 3 и 5; 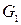 ,
, 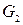 ,
, 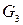 ,
, 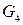 ,
, 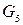 - силы тяжести звеньев;
- силы тяжести звеньев; 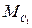 - приложенный к звену 1 момент сопротивления со стороны той рабочей машины, которую приводит в движение двигатель. Начальный звеном механизма является коленчатый вал двигателя - звано 1, имеющее угловую координату
- приложенный к звену 1 момент сопротивления со стороны той рабочей машины, которую приводит в движение двигатель. Начальный звеном механизма является коленчатый вал двигателя - звано 1, имеющее угловую координату 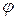 и вращающееся с угловой скоростью
и вращающееся с угловой скоростью 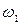 . Звено динамической модели имеет угловую координату
. Звено динамической модели имеет угловую координату 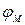 и вращается с угловой скоростью
и вращается с угловой скоростью 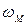 . В каждый момент времени координаты и их производные по времени совпадают:
. В каждый момент времени координаты и их производные по времени совпадают: 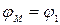 ;
; 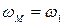 .
.
Для определения величины приведенного момента 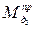 , заменяющего движущую силу
, заменяющего движущую силу 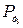 , воспользуемся формулой (25), которая примет вид
, воспользуемся формулой (25), которая примет вид
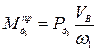 (27)
(27)
так как
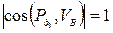
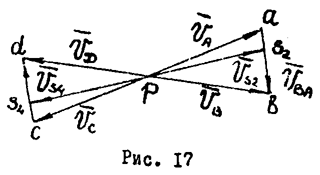 Передаточную функцию
Передаточную функцию 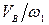 , найдем, построив для рассматриваемого положения механизма план возможных скоростей (т.е. без масштаба, для произвольной величины
, найдем, построив для рассматриваемого положения механизма план возможных скоростей (т.е. без масштаба, для произвольной величины 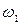 , задавшись постоянный отрезком
, задавшись постоянный отрезком 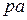 ) (рис. 17). Тогда
) (рис. 17). Тогда
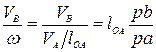
где 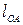 - длина кривошипа;
- длина кривошипа;
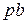 и
и 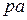 - отрезки, изображающие скорости
- отрезки, изображающие скорости 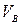 и
и 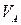 .
.
Величину силы 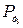 в каждом положении механизма следует взять из построенного ранее графика
в каждом положении механизма следует взять из построенного ранее графика 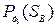 (см. рис.13). Знак момента
(см. рис.13). Знак момента 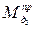 определяется знаком силы
определяется знаком силы 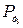 . Момент
. Момент 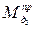 следует вычислить для каждого положения механизма и затем построить график изменения приведенного момента
следует вычислить для каждого положения механизма и затем построить график изменения приведенного момента 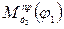 .
.
На графиках приведенных моментов здесь и далее по оси абсцисс следует откладывать угол поворота 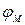 - звена динамической модели. Для нашего примера в каждый момент времени
- звена динамической модели. Для нашего примера в каждый момент времени 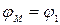 (
(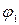 - угол поворота начального звена 1). Угол
- угол поворота начального звена 1). Угол 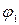 удобно отсчитывать от мертвого положения механизма, принятого за начальное. Так как цикл работы механизма в рассматриваемом случае равен двум оборотам звена 1, то по оси абсцисс следует отложить угол
удобно отсчитывать от мертвого положения механизма, принятого за начальное. Так как цикл работы механизма в рассматриваемом случае равен двум оборотам звена 1, то по оси абсцисс следует отложить угол 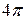 рад. Если база графика равна b мм, то масштаб по оси абсцисс равен
рад. Если база графика равна b мм, то масштаб по оси абсцисс равен 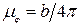 мм/рад.
мм/рад.
Масштаб по оси ординат графика 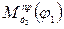 назначается с учетом желаемой максимальной ординаты:
назначается с учетом желаемой максимальной ординаты:
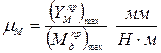 (28)
(28)
Заметим, что в тех машинах (двухтактный двигатель внутреннего сгорания, компрессор, ковочный пресс и др.), где продолжительность цикла равна одному обороту начального звена, по оси абсцисс следует отложить угол 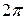 рад.
рад.
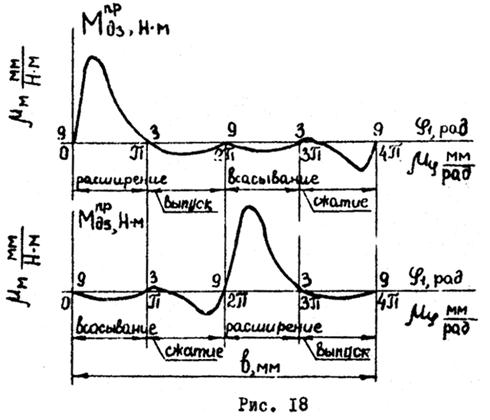
Примерный вид графика 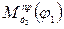 представлен на рис. 18.
представлен на рис. 18.
Результаты расчета рекомендуется поместить в расчетно-пояснительной записке в виде таблицы по следующему образцу
| Величина | Размерность | Положения механизма | |||
| … | |||||
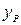 | мм | ||||
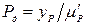 | Н | ||||
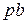 | мм | ||||
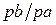 | – | ||||
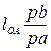 | м | ||||
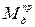 | 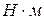 |
Момент 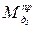 , заменяющий силу
, заменяющий силу 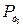 , определяется аналогично. График
, определяется аналогично. График 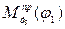 построен с учетом того, что рабочий процесс в правом цилиндре сдвинут по фазе на угол
построен с учетом того, что рабочий процесс в правом цилиндре сдвинут по фазе на угол 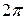 по отношению к процессу в левом цилиндре (рис. 18).
по отношению к процессу в левом цилиндре (рис. 18).
При построении графиков приведенных моментов для многоцилиндровых машин следует обязательно учитывать угол сдвига фаз рабочих процессов в цилиндрах машины.
Найдем приведенные моменты, заменяющие силы тяжести звеньев.
Приведенный момент 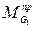 , заменяющий силу тяжести
, заменяющий силу тяжести 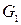 звена 1, равен
звена 1, равен
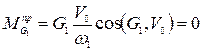
так как скорость точки O 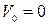 .
.
Приведенный момент 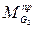 , заменяющий силу тяжести
, заменяющий силу тяжести 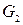 звена 2, равен
звена 2, равен
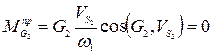 (29)
(29)
где отношение скоростей 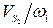 находим с помощью плана возможных скоростей по формуле
находим с помощью плана возможных скоростей по формуле
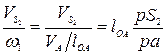
Так как 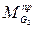 зависит от положения механизма, то следует найти его значение для каждого положения и затем построить график
зависит от положения механизма, то следует найти его значение для каждого положения и затем построить график 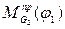 .
.
Аналогично определяется приведенный момент 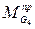 , заменяющий силу тяжести
, заменяющий силу тяжести 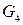 звена 4.
звена 4.
Приведенный момент 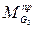 , заменяющий силу тяжести
, заменяющий силу тяжести 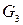 звена 3, равен
звена 3, равен
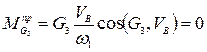
так как 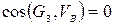
Аналогично 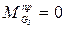 .
.
Во многих машинах приведенные моменты от сил тяжести звеньев малы (по сравнению с приведенными моментами от сил движущих и сопротивления) и ими можно пренебречь.
Приведенный момент 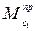 , заменяющий момент сопротивления
, заменяющий момент сопротивления 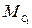 найдем по формуле (26), которая примет вид
найдем по формуле (26), которая примет вид
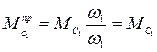 (30)
(30)
В данном случае приведенный момент 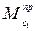 равен действительному монету
равен действительному монету 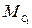 , так как последний приложен к начальному звену.
, так как последний приложен к начальному звену.
Зная в каждом положении механизма величины приведенных моментов, можно, сложив их алгебраически, получить суммарный приведенный момент
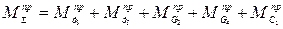 (31)
(31)
и построить график 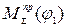 .
.
Момент 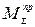 , приложенный к звену динамической модели, производит ту же роботу, что и все реальные силы и моменты, приложенные к различным звеньям механизма.
, приложенный к звену динамической модели, производит ту же роботу, что и все реальные силы и моменты, приложенные к различным звеньям механизма.
б) Метод приведения масс
В основу метода приведения масс положено условие равенства кинетической энергии всех звеньев механизма и звена динамической модели. В этом случае закон движения последнего будет таким же, как и закон движения начального звена реального механизма.
Для определения приведенного момента инерции 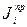 каждого звена механизма необходимо составить равенство кинетических энергий рассматриваемого звена и звена модели.
каждого звена механизма необходимо составить равенство кинетических энергий рассматриваемого звена и звена модели.
В зависимости от характера движения звена существуют следующие варианты равенстве кинетических энергий:
1. При поступательном движении i-го звена механизма
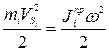 ,
,
откуда
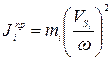 (32)
(32)
2. При вращательном движении звена вокруг неподвижной оси K
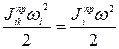 ,
,
откуда
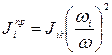 (33)
(33)
3. При плоскопараллельном движении звена
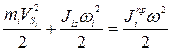
откуда
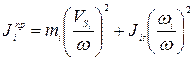 (34)
(34)
где 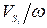 ,
, 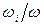 - передаточные функции.
- передаточные функции.
Суммарный приведенный момент инерции всего механизма равен сумме приведенных моментов инерции всех его звеньев и зависит от положения механизма:
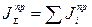 (35)
(35)
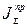 зависит от отношения скоростей и может определяться без учета действительного закона движения звеньев.
зависит от отношения скоростей и может определяться без учета действительного закона движения звеньев.
В качества примера определим суммарный приведенный момент инерции механизма, изображенного на рис. 13. Звено 1 - начальное звено механизма. Приведенный момент инерции звена 3 находится по формуле
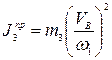
Заменяя 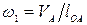 и переходя к отрезкам, взятым из плана возможных скоростей, получил
и переходя к отрезкам, взятым из плана возможных скоростей, получил
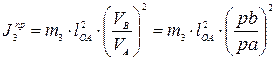 (36)
(36)
Аналогично для звена 5
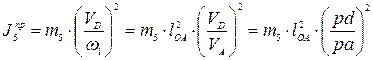
Приведенный момент инерции звена 2 определится по формуле
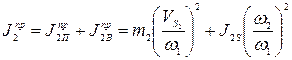
Заменяя 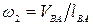 и переходя к отрезкам, получим
и переходя к отрезкам, получим
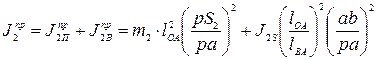 (37)
(37)
Аналогично для звена 4
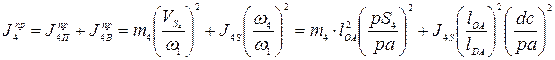
Рекомендуется предварительно подсчитать величины, не зависящие от положения механизма, например 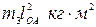 ;
; 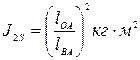 и т.д.
и т.д.
Результаты расчета для каждого 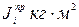 заносят в таблицу и помещают в расчетно-пояснительной записке.
заносят в таблицу и помещают в расчетно-пояснительной записке.
| Величина | Размерность | Положения механизма | |||
| … | |||||
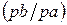 | – | ||||
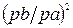 | – | ||||
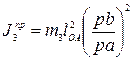 | 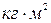 |
Приведенный момент инерции звена 1 определится по формуле
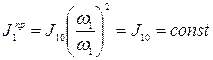 (38)
(38)
Суммарный приведенный момент инерции всего механизма
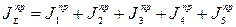 (39)
(39)
Построив графики приведенных моментов инерции отдельных звеньев 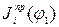 масштабе
масштабе 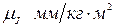 , можно получить график суммарного приведенного момента инерции
, можно получить график суммарного приведенного момента инерции 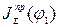 .
.
 2015-04-01
2015-04-01 2332
2332
