Количеством движения системы будем называть векторную величину 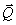 , равную геометрической сумме (главному вектору) количеств движения всех точек системы (рис.44):
, равную геометрической сумме (главному вектору) количеств движения всех точек системы (рис.44):
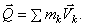
Из чертежа видно, что независимо от величин скоростей точек системы (если только эти скорости не параллельны) вектор 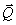 может принимать любые значения и даже оказаться равным нулю, когда многоугольник, построенный из векторов
может принимать любые значения и даже оказаться равным нулю, когда многоугольник, построенный из векторов 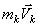 , замкнется. Следовательно, по величине
, замкнется. Следовательно, по величине 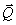 нельзя полностью судить о характере движения системы.
нельзя полностью судить о характере движения системы.
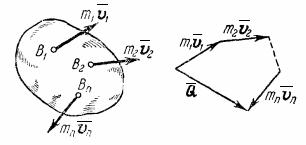
Рис.44
Найдем формулу, с помощью которой значительно легче вычислять величину 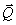 , а также уяснить ее смысл.
, а также уяснить ее смысл.
Из равенства 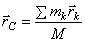 следует, что
следует, что 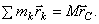
Беря от обеих частей производную по времени, получим
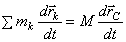 или
или 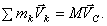
Отсюда находим, что 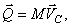
т.е. количество движения системы равно произведению массы всей системы на скорость ее центра масс. Этим результатом особенно удобно пользоваться при вычислении количеств движения твердых тел.
Из формулы видно, что если тело (или система) движется так, что центр масс остается неподвижным, то количество движения тела равно нулю. Например, количество движения тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс, будет равно нулю.
Если же движение тела является сложным, то величина 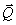 не будет характеризовать вращательную часть движения вокруг центра масс. Например, для катящегося колеса
не будет характеризовать вращательную часть движения вокруг центра масс. Например, для катящегося колеса 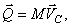 независимо от того, как вращается колесо вокруг его центра масс С.
независимо от того, как вращается колесо вокруг его центра масс С.
Таким образом, количество движения характеризует только поступательное движение системы. При сложном же движении величина 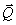 характеризует только поступательную часть движения системы вместе с центром масс.
характеризует только поступательную часть движения системы вместе с центром масс.
 2015-05-06
2015-05-06 910
910








