Теорема об изменении кинетической энергии системы

Если рассмотреть какую-нибудь точку системы с мас­сой 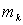, имеющую скорость 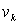, то для этой точки будет

,

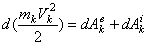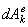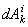где и - элементарные работы действующих на точку внеш­них и внутренних сил. Составляя такие уравнения для каждой из точек системы и складывая их почленно, получим

,

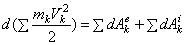или

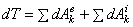. (2)

Равенство выражает теорему об изменении кине­тической энергии системы в дифференциальной форме.

Если полученное выражение отнести к элементарному промежутку времени, в течение которого произошло рассматриваемое перемещение, можно получить вторую формулировку для дифференциальной формы теоремы: производная по времени от кинетической энергии механической системы равна сумме мощностей всех внешних (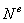) и внутренних (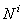) сил, т.е.

.

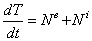Дифференциальными формами теоремы об изменении кинетической энергии можно воспользоваться для составления дифференциальных уравнений движения, но это делается достаточно редко, потому что есть более удобные приемы.

Проинтегрировав обе части равенства (2) в пределах, соответствующих перемещению системы из некоторого начального положения, где кинетическая энергия равна 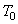, в положение, где значение кинетической энергии становится равным 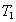, будемиметь

.

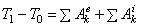Полученное уравнение выражает теорему об изменении кинетической энергии в конечном виде: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом пере­мещении всех приложенных к системе внешних и внутренних сил.

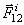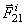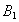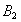В отличие от предыдущих теорем, внутренние силы в уравнениях не исключаются. В самом деле, если и - силы взаимодействия между точками и системы (см. рис.51), то 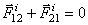. Но при этом точка 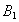, может перемещаться по направ­лению к 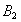, а точка 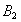- по направлению к 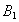. Работа каждой из сил бу­дет тогда положительной и сумма работ нулем не будет. Примером мо­жет служить явление отката. Внутренние силы (силы давления), действующие и на снаряд и на откатывающиеся части, совершают здесь положительную работу. Сумма этих работ, не равная нулю, и изменяет кинетическую энергию системы от вели­чины 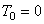в начале выстрела до величины 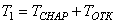конце.

Другой пример: две точки, соединенные пружиной. При изменении расстояния между точками упругие силы, приложенные к точкам, будут совершать работу. Но если система состоит из абсолютно твердых тел и связи между ними неизменяемые, не упругие, идеальные, то работа внутренних сил будет равна нулю и их можно не учитывать и вообще не показывать на расчетной схеме.

Рассмотрим два важных частных случая.

1) Неизменяемая система. Неизменяемой будем называть систему, в которой расстояния между точками приложения внутрен­них сил при движении системы не изменяются. В частности, такой системой является абсолютно твердое тело или нерастяжимая нить.

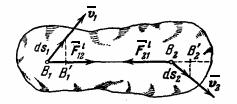
Рис.51

Пусть две точк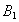и и 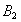неизменяе­мой системы (pис.51), действующие друг на друга с силам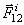и и 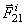(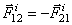) имеют в данный момент скорост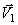и и 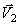. Тогда за промежу­ток времени dt эти точки совершат элементарные перемещения 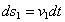и 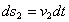, направленные вдоль векторов 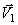и 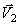. Но таккак отрезок 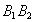является неизменяемым, то по известной теореме кинематики про­екции векторов 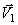и 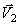,а, следовательно, и перемещени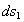й и 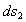на направление отрезка 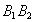будут равны друг другу, т.е. 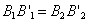. Тогда элементарные работы сил 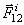и 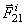будут одинаковы по мо­дулю и противоположны по знаку и в сумме дадут нуль. Этот резуль­тат справедлив для всех внутренних сил при любом перемещении системы.

Отсюда заключаем, что для неизменяемой системы сумма работ всех внутренних сил равна нулю и уравнения принимают вид

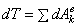или .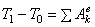

2) Система с идеальными связями. Рассмотрим систему, на которую наложены связи, не изменяющиеся со временем. Разделим все действующие на точки системы внешние и внутренние силы на активные и реакции связей. Тогда

,

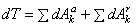где 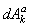- элементарная работа действующих на k- ю точку системы внешних и внутренних активных сил, a 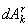- элементарная работа реакций наложенных на ту же точку внешних и внутренних связей.

Как видим, изменение кинетической энергии системы зависит от работы и активных сил и реакций связей. Однако можно ввести по­нятие о таких «идеальных» механических системах, у которых нали­чие связей не влияет на изменение кинетической энергии системы при ее движении. Для таких связей должно, очевидно, выполняться условие:

.

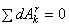Если для связей, не изменяющихся со временем, сумма работ всех реакций при элементарном перемещении системы равна нулю, то такие связи назы­вают идеальными. Для механической системы, на которую наложены только не изменяющиеся со временем идеальные связи, будем, очевидно, иметь

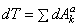или .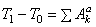

Таким образом, изменение кинетической энергии системы с идеальными, не изменяющимися со временем связями при любом ее перемещении равно сумме работ на этом перемещении, приложенных к системе внешних и внутренних активных сил.

Механическая система называется консервативной (энергия ее как бы законсервирована, не изменяется), если для нее имеет место интеграл энергии

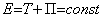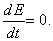или (3)

Это есть закон сохранения механической энергии: при движении системы в потенциальном поле механическая энергия ее (сумма потенциальной и кинетической) все время остается неизменной, постоянной.

Механическая система будет консервативной, если действующие на нее силы потенциальны, например сила тяжести, силы упругости. В консервативных механических системах с помощью интеграла энергии можно проводить проверку правильности составления дифференциальных уравнений движения. Если система консервативна, а условие (3) не выполняется, значит при составлении уравнений движения допущена ошибка.

Интегралом энергии можно воспользоваться для проверки правильности составления уравнений и другим способом, без вычисления производной. Для этого следует после проведения численного интегрирования уравнений движения вычислить значение полной механической энергии для двух различных моментов времени, например, начального и конечного. Если разница значений окажется сопоставимой с погрешностями вычислений, это будет свидетельствовать о правильности используемых уравнений.

Все предыдущие теоремы позволяли исключить из уравнений движения внутренние силы, но все внешние силы, в том числе и наперед неизвестные реакции внешних связей, в уравнениях сохранялись. Практическая ценность теоремы об изменении кинетической энергии состоит в том, что при не изменяющихся со временем идеальных связях она позволит исключить из уравнений движения все наперед неизвестные реакции связей.

Теорему об изменении кинетической энергии удобно использовать при решении задач, в которых требуется установить зависимость между скоростями и перемещениями тел.

Пример 13. Какую скорость надо сообщить точке М стержня, прикрепленного верхним концом с помощью шарнира О к неподвижной поверхности (рис.52), чтобы стержень совершил четверть оборота?

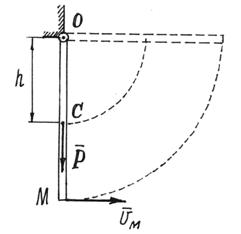
Рис.52

В первом, вертикальном, положении кинетическая энергия стержня, начавшего вращаться вокруг оси О,

.

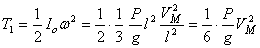Во втором положении, где стержень достигнет горизонтального положения и остановится на мгновение, Т ₂ = 0.

Работу совершит только вес стержня Р: 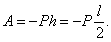По теореме получим уравнение 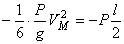, из которого следует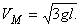

Пример 14. Механическая система состоит из двух шаров A и B, связанных с шарниром O и ползуном C невесомыми стержнями.

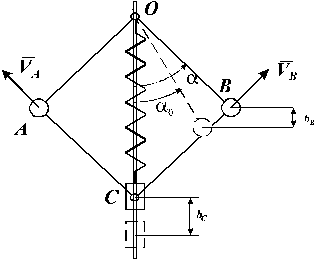
Рис.53

Массы шаров и ползуна одинаковы и равны 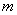=0,2 кг. Стержни имеют одинаковую длину 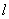= 0,3 м. Между шарниром и ползуном установлена пружина жесткостью c =100 Н/м, длина которой в недеформированном состоянии равна 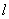(рис.53) Требуется определить зависимость скоростей движения шаров от угла отклонения стержней от вертикали 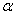и найти максимальное отклонение, если в начальный момент времени система покоилась, а угол 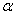составлял .

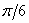Кинетическая энергия системы складывается из кинетических энергий трех тел, которые по условию могут рассматриваться как материальные точки.

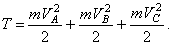(4)

Скорости шаров пропорциональны угловой скорости вращения стержней OA и OB

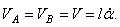
Скорость ползуна нетрудно определить, если учесть, что

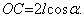
Тогда

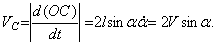
Подставляя выражения для скоростей в (4), получим зависимость кинетической энергии системы от скоростей шаров V и угла отклонения стержней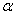

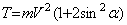. (5)

Определим работу, которую совершат все силы, приложенные к системе при ее перемещении из начального положения в конечное. Работа сил тяжести определяется вертикальными перемещениями центров тяжести тел (см. рис.53):

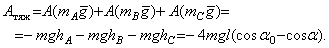(6)

Для вычисления работы силы упругости воспользуемся формулой:

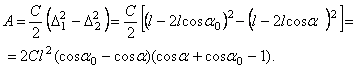(7)

Подставляя выражения (5), (6) и (7) в уравнение теоремы об изменении кинетической энергии, получаем зависимость скорости движения шаров от угла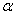

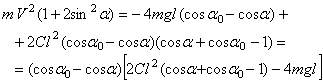
или в явном виде

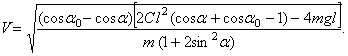(8)

Если в уравнении 8 скорость V приравнять нулю, можно найти два предельных значения угла 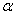, между которыми будет происходить движение системы при заданным начальных условиях:

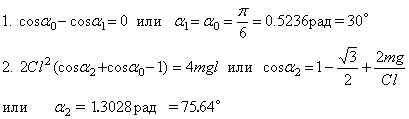
Лекция 7. Приложение общих теорем к динамике твердого тела.

В данной лекции рассматриваются следующие вопросы:

1. Принцип Даламбера.

2. Главный вектор и главный момент сил инерции твердого тела.

3. Вращательное движение твердого тела.

4. Физический маятник.

5. Плоскопараллельное движение твердого тела.