Максвел теоретически решил задачу о распределении молекул по скоростям поступательного движения. Он установил закон позволяющий определять какое число молекул 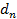 из общего числа молекул
из общего числа молекул 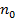 находящихся в единице объема при данной температуре t имеет скорости лежащие в интервале от
находящихся в единице объема при данной температуре t имеет скорости лежащие в интервале от 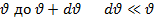
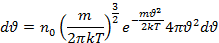
Записанное соотношение позволяет определить наиболее вероятную скорость. Наиболее вероятной скорости соответствует значение скорости 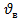 , которым и близкими к ней скоростями обладает наибольшее число молекул. Чтобы найти наиболее вероятную скорость необходимо найти max ф-ции
, которым и близкими к ней скоростями обладает наибольшее число молекул. Чтобы найти наиболее вероятную скорость необходимо найти max ф-ции 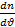
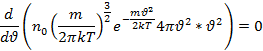
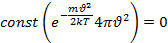
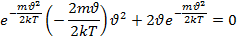
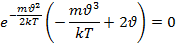
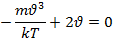

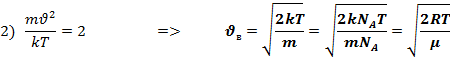
40. 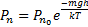 мы получили барометрическую фор-лу установ. Зависимость давления газа от высоты.
мы получили барометрическую фор-лу установ. Зависимость давления газа от высоты.
41. Учитывая, что давление пропорционально концентрации 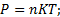
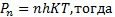
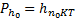 ;
; 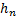 KT=
KT= 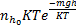 ;
; 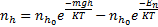 ; полученное соотношение оказывается справедливым в любом поле и наз. распределением Больцмана.
; полученное соотношение оказывается справедливым в любом поле и наз. распределением Больцмана.
42. Молекулы одноатомного газа можно рассматривать как материальные точки, а материальная точка имеет три степени свободы, т.е. три величины, определяющие положение материальной точки в пространстве.
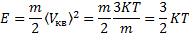
Тогда энергия приходящаяся на на одну степень свободы равно вероятностный характер движения будет равен 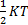
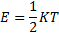
Вывод: на каждую степень свободы поступательного движения молекул приходить энергия равная 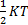 - закон равномерного распределения энергии по степеням свободы. Если молекула имеет i степеней свободы = 3 (для одноатомного газа) 5 (для двухатомного) и 6 (для трех и многоатомного) то её энергия будет равна
- закон равномерного распределения энергии по степеням свободы. Если молекула имеет i степеней свободы = 3 (для одноатомного газа) 5 (для двухатомного) и 6 (для трех и многоатомного) то её энергия будет равна 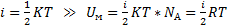
43. Закон сохранения энергии для теплоты как форма внутренней энергии к работе с учетом условия знака может быть записана в следующем виде:
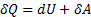
Кол-во теплоты сообщенном системе идет на изменение внутренней энергии системы и на совершение системы работы над внешними телами.
Кол-во теплоты, которое поступает в систему принято считать положительной. Работа которая совершилась системой над внешними телами называется положительной.
Если внутренняя энергия возрастает, то изменение внутренней энергии считается положительной.
Если произвольная величина f явл. функцией состояния, т.е. функцией которая в заданном состоянии системы имеет определенное значение не зависимо от того, каким путем или способом в это состояние система приведена, то она явл. полным дифференциалом и обозначается буквой d, в противном случае 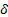
Функциями состояния в термодинамике явл. P,V,T внутренняя энергия, энтропия и др.
44. а) А при изотермическом 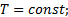
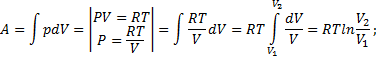
б) изохорный  =const;
=const;
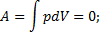
в) изобарный 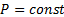 ;
;
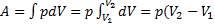 );
);
45. При сообщении телу кол-ва теплоты 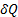 температура тела изменится на величину
температура тела изменится на величину 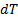 , тогда величина
, тогда величина 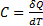 - называется теплоемкостью тела. Теплоемкость отнесенная к единице массы тела наз. удельной и используется при изучении тепловых процессов в твердых телах и жидкостях.
- называется теплоемкостью тела. Теплоемкость отнесенная к единице массы тела наз. удельной и используется при изучении тепловых процессов в твердых телах и жидкостях.
Теплоемкость, отнесенная к молю в-ва наз. молярной и используется при исследовании тепловых процессов в газах.
Как видно из формулы 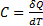 теплоемкость не является функцией состояния. Рассмотрим теплоемкость при постоянном объёме.
теплоемкость не является функцией состояния. Рассмотрим теплоемкость при постоянном объёме.
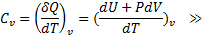
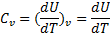
Учитывая что внутренняя энергия моля газа 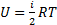
При постоянном давлении:
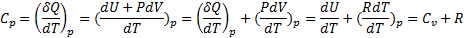
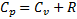 - ур-е Майера
- ур-е Майера
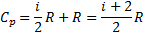
46. Процесс, протекающий без теплообмена с окружающей средой наз. адиабатным.
Адиабатный процесс для законов термодинамики.
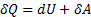
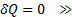
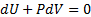
Уравнение связывающие параметры состоянии газа в адиабатном процессе наз. уравнением адиабаты, или уравнением Пуассона.
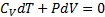
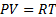
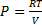
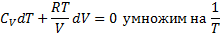
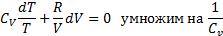
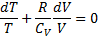
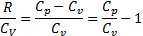
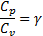
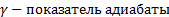
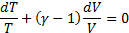
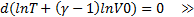
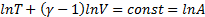
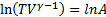
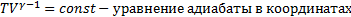
47. Работа в адиабатном процессе.
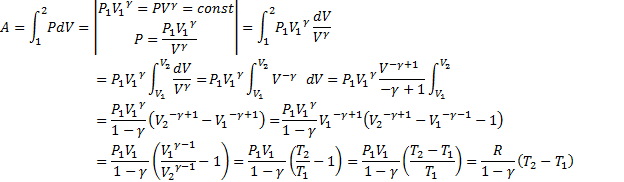
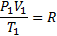
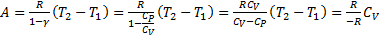 (
( 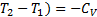 (
( 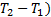
_____________________________________
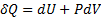
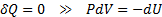
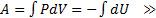
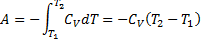
48. 1.Работа при изотермическом процессе.
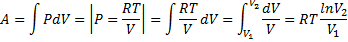
2. Работа при изохорном процессе.
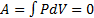 т.к. V=0
т.к. V=0
3. Работа при изобарном процессе.
P=const
Циклическим наз. процесс, начало и конец которого совпадает.
Наиболее простым но важным явл. цикл Карно состоящий из двух изотерм и двух адиабат.

Направление цикла Карно указано стрелками.
Участок 1-2 явл. участком изотермического расширения при температуре 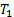 . Участок 2-3 явл. участком адиабатного процесса расширения в отсутствие теплообмена с окружающей средой. 3-4 участок изотермического сжатия при температуре
. Участок 2-3 явл. участком адиабатного процесса расширения в отсутствие теплообмена с окружающей средой. 3-4 участок изотермического сжатия при температуре 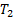 .
.
Нарисованный рисунок явл. прямым и соответствует работе тепловой машины, которая выполняет работу за счёт теплоты, получаемой из термостата с более высокой 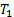 .
.
Термостат с температурой 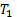 наз. нагревателем, а термостат с температурой
наз. нагревателем, а термостат с температурой 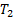 – холодильником.
– холодильником.
49. Энтропия - отношение теплоты к температуре, при которой происходит переход энергии.
Энтропия определяет направление протекания процесса в термодинамических системах и как правило процессы всегда с возрастанием энтропии.
Воспользуемся первым началом термодинамики:
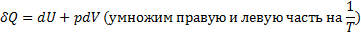
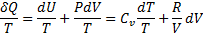
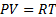
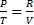
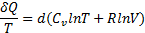
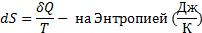
50. Изменение энтропии при изотермическом процессе.
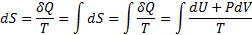
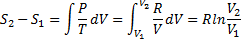
Изменение энтропии при изохорном процессе V=const
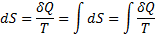
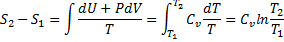
При изобарном процессе изменение энтропии равно сумме изменения энтропии при изотермическом и изохорном процессе.
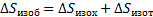
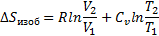
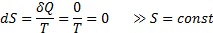
 2015-04-20
2015-04-20 742
742